Review of Chemical Bonding
Shaun Williams, PhD
Basics of Valence Bond Theory
- All matter is composed of atoms
- Atoms may be bonded to other atoms to form molecules
- The Lewis Structure is a simple way to represent molecular structures
- The Octet Rule: The octet rule is a rule of thumb that atoms of main-group elements tend to combine in such a way that each atom has eight valence electrons in its valence shell
The Octet Rule
- The octet rule can be rationalized for s- and p-block elements because they have four valence orbitals accommodating up to 8 valence electrons.
- A pair of shared electrons is a single line - a single bond
- Two pair of shared electrons is two lines - a double bond
- Three pair of shared electrons is three lines - a triple bond
- Any pairs of electrons not bond are lone pairs on a single atom
Examples of Lewis Structures

Analysis of Lewis Structures
- Lewis Structures are powerful in their simplicity
- It can be used to predict combining ratios of atoms and to sort plausible from implausible structures
- It can be used to rationalize the acid-base properties of molecules
- The model, however, is built on shaky, pre-quantum mechanical description of atoms
- That means it will make mistakes
- Let's see how far we can push Lewis Structures (the Localized Electron Model)
Example 1.1
Construct the Lewis Dot diagram for the nitrate ion, NO−3.
Formal Charge
- Note the formal charge issues in the nitrate example
- Note: formal charge is not the same thing as the oxidation number (or oxidation state)
- The formal charge is typically close to the "real" charge on the atom
- Oxidation states are useful for keeping track of oxidation-reduction reactions
- Like oxidation states, the formal charges of the atoms in a molecule or ion must add up to its overall charge.
Using Formal Charges
When we have more than one valence bond structure which are possible, we can use formal charges to decide which structure should be more or less stable using the following rules
- The formal charges on atoms are minimized in stable structures, zero being the best case.
- Negative formal charges should be placed on the most electronegative atom(s).
- Positive formal charges should be placed on the least electronegative atom(s).
- It is unfavorable to place like charges (++ or --) on neighboring atoms in a molecule.
Example 1.2: BF3
Which is more stable? Why?
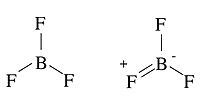
Example 1.3: ONF
Which is more stable? Why?
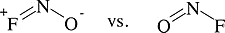
Resonance Structures
The ozone (O3) molecule has two equivalent octet structures

- In both structures, the formal charges are exactly the same
- While the structures also suggest that ozone has a single bond and a double bond
- Experimentally, however, the molecule is symmetric with both O-O bonds the same lengths.

What is Resonance?
Resonance is a way of describing delocalized electrons within certain molecules or polyatomic ions where the bonding cannot be expressed by one single Lewis structure. A molecule or ion with such delocalized electrons is represented by several contributing structures.
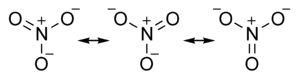
Resonance in the Nitrate Ion
The nitrate ion can be represented as three structures
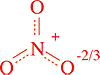
These give rise to an average structure
Inequivalent Resonance Structures
- The rules of resonance also apply to inequivalent structures, which will generally have different energies
- The structure represents a weighted average of the low energy structures
- For example, the cyanate ions have three inequivalent octet structures
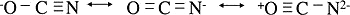
- The first two are likely much more stable so the average structure will be a weighted average of these two.
No-Bond Resonance
- An interesting and useful kind of nonequivalent resonance structure is one in which there is a bond order of zero between two of the atoms.
- This no-bond resonance is important in understanding the bonding in many halogen and hydrogen containing compounds.
- Considering the following general compounds were Z might be a electronegative halogen atom

- These two structures imply that the X-Y bond order is 1.5 and the Y-Z bond order is 0.5.
Example 1.4: No-Bond Resonance
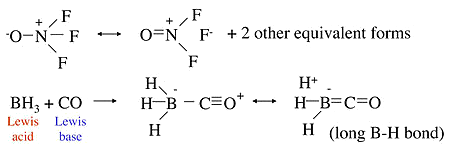
- In the molecule ONF3, the N-F bond is unusually long relative to the N-F bond in NF3, in which the bond order is 1.
- This can be explained by the no-bond resonance forms below
- Similarly, in the Lewis acid-base adduct formed by combining BH3 and CO, we can explain the long B−H bonds
Example 1.5: I−3
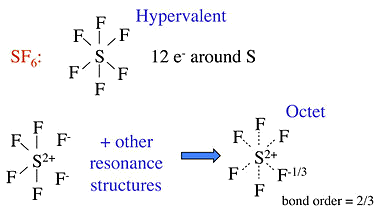
- No-bond resonance is often used to provide an octet bonding picture for hypervalent compounds
- Raman spectra of the triiodide ion show that the I-I bond is weaker than the I-I single bond in I2.
- This suggests that the above picture is incorrect
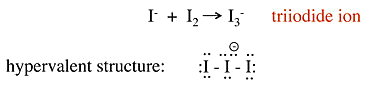
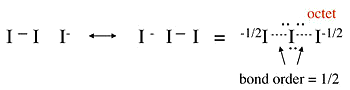
Other Hypervalent Molecules
- We can draw the structure XeF2 molecule like that of I−3.
- Other structures which need the no-bond resonance are PF5, P(CH3)5, and SF6, as well as oxyacids such as H2SO4 and HClO4.
- The hypervalent structure drawn for these are often explained with d-orbitals on the central atom - giving dsp3 and d2sp3 hybrid orbitals
Hypervalent Examples
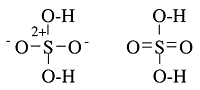
The Isoelectronic Principle
- In calculating the octet structures, we needed to know only the number of atoms and the number of electrons
- This means that we will get the same answer for any molecule or ion that contains
- the same number of non-hydrogen atoms and
- the same total number of valence electrons
- These molecules are said to be isoelectronic
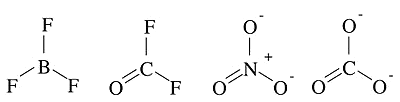
Isoelectronic Examples
Set 1:

Set 2:
Isoelectronic Solids
- The isoelectronic principle also works for extended solids
- One technologically important set of isoelectronic solids are the p-block semiconductors
- The group 14 element Si is the most widely used semiconductor for electronics but it is not a good light emitter
- Light-emitting diodes (LEDs), are made from compounds that are isoelectronic with Si and Ge, especially GaAs, GaP, AlAs, and GaN
- CdTe and CuIn1−xGaxSe2 (CIGS) are promising solar cell materials that also have the same number of valence electrons per atom.
Important of the Isoelectronic Principle
- The isoelectronic principle is a powerful tool in materials research because it provides guidance about where to look for new materials with similar properties
- The discovery that 8.5% efficient thin layer solar cells could be made from CsSnI3 stimulated the exploration of many isoelectronic ABX3 compounds with the same perovskite crystal structure
- Very recent solar cells in this family based on CH3NH3PbI3−xClx have been reported with efficiencies as high as 14-15%.
The shapes of molecules (VSEPR theory) and orbital hybridization
- The VSEPR theory is a simple and useful way to predict and rationalize the shapes of molecules
- It is based on the idea of minimizing the electrostatic repulsion between electron pairs
Using VSEPR
- First we begin with a Lewis dot structure
- VSEPR considers all bonding domains equally (ie. a single bond, double bond, triple bond, half bond all count as one electron domain)
- You can use either an octet or hypervalent structure, provided that the number of lone pairs (which should be the same in both) is calculated correctly
Obtaining Electronic Geometry
- Determine the number of lone pairs on the central atom in the molecule and add the number of bonded atoms (a.k.a. bonding domains).
- This number (known as the steric number) defines the electronic shape of the molecule by minimizing repulsion. For example a steric number of three gives a trigonal planar electronic shape.
- The angles between electron domains are determined primarily by the electronic geometry (eg., 109.5∘ for steric number 4, which implies that the electronic shape is a tetrahedron)
- These angles are adjusted by the hierarchy of repulsions: (lone pair - lone pair) > (lone pair - bond) > (bond - bond)
Note of Repulsion Hierarchy
The hierarchy of repulsions can also be used to rationalize which sites lone pairs and ligands occupy in molecules with a large steric number and few ligands/many lone pairs. This can be observed in the table below and is further covered below in the geometrical isomers subsection with the XeF2 molecule.
Molecular Geometry
- Molecular geometry is deduced from the electronic geometry by considering the lone pairs to be present but invisible.
- The most commonly used method to determine molecular structure (X-ray diffraction, neutron diffraction, and electron diffraction) have a hard time seeing lone pairs
- These methods can accurately determine the lengths of bonds between atoms and the bond angles
Structure Properties
| Bonding electron pairs | Lone pairs | Electron domains (Steric #) | Shape | Ideal bond angle (example's bond angle) | Example | Image |
|---|---|---|---|---|---|---|
| 2 | 0 | 2 | linear | 180∘ | CO2 |  |
| 3 | 0 | 3 | trigonal planar | 120∘ | BF3 |  |
| 2 | 1 | 3 | bent | 120∘ (119∘) | SO2 | 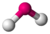 |
| 4 | 0 | 4 | tetrahedral | 109.5∘ | CH4 | 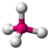 |
Structure Properties Continued
| Bonding electron pairs | Lone pairs | Electron domains (Steric #) | Shape | Ideal bond angle (example's bond angle) | Example | Image |
|---|---|---|---|---|---|---|
| 3 | 1 | 4 | trigonal pyramidal | 109.5∘ (107∘) | NH3 | 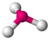 |
| 2 | 2 | 4 | bent | 109.5∘ (104.5∘) | H2O | 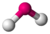 |
| 5 | 0 | 5 | trigonal bipyramidal | 90∘, 120∘, 180∘ | PCl5 | 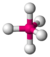 |
| 4 | 1 | 5 | seesaw | 90∘, 120∘, 180∘ (173.1∘, 101.6∘) | SF4 | 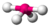 |
Structure Properties Even More
| Bonding electron pairs | Lone pairs | Electron domains (Steric #) | Shape | Ideal bond angle (example's bond angle) | Example | Image |
|---|---|---|---|---|---|---|
| 3 | 2 | 5 | T-shaped | 90∘, 180∘ (87.5∘, <180∘) | ClF3 | 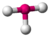 |
| 2 | 3 | 5 | linear | 180∘ | XeF2 |  |
| 6 | 0 | 6 | octahedral | 90∘, 180∘ | SF6 | 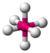 |
| 5 | 1 | 6 | square pyramidal | 90∘ (84.8∘), 180∘ | BrF5 | 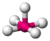 |
Structure Properties... Yeah, still going
| Bonding electron pairs | Lone pairs | Electron domains (Steric #) | Shape | Ideal bond angle (example's bond angle) | Example | Image |
|---|---|---|---|---|---|---|
| 4 | 2 | 6 | Square planar | 90∘, 180∘ | XeF4 | 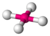 |
| 7 | 0 | 7 | pentagonal bipyramidal | 90∘, 72∘, 180∘ | IF7 | 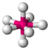 |
| 6 | 1 | 7 | pentagonal pyramidal | 72∘, 90∘, 144∘ | XeOF−5 | 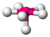 |
| 5 | 2 | 7 | planar pentagonal | 72∘, 144∘ | XeF−5 | 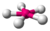 |
Structure Properties... Hey look, finally finishing
| Bonding electron pairs | Lone pairs | Electron domains (Steric #) | Shape | Ideal bond angle (example's bond angle) | Example | Image |
|---|---|---|---|---|---|---|
| 8 | 0 | 8 | Square antiprismatic | XeF2−8 |  |
|
| 9 | 0 | 9 | tricapped trigonal prismatic | ReH2−9 |  |
- The deviations from the ideal bond angles can be rationalized by utilizing the hierarchy of repulsion.
Geometrical Isomers
- In the previous tables, many molecules have more than one possible shape that would satisfy the VSEPR rules
- Examples, XeF2 has steric number of five and a trigonal bipyramidal geometry
- There are three possible stereoisomers: one in which the F atoms occupy axial sites (linear), one in which the F atoms occupy one equatorial and one axial site (90∘ bond angle), and one in which the F atoms are both equatorial (bond angle 120∘).
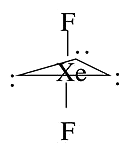
XeF2 Isomers
- If we place one F equatorial we would have a structure where one of the lone pairs is axial and the other two are equatorial
- The axial lone pair would have an angle of 90∘ with the equatorial lone pairs
- The equatorial lone pairs would have an angle of 120∘ with each other
- We need to find the condition which is the least unfavorable as it is very unfavorable for the lone pairs to be bunched up more closely than necessary
- If both fluorines are equatorial then more of the lone pairs are 90∘ angles with each other
- In the linear isomer, all of the electrons are 120∘ separated from each other - the best case
Example 1.6: The BrF−4 Interhalide Ion
The BrF−4 anion is isoelectronic with XeF4. What is its shape?
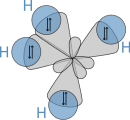
Orbital Hybridization
- When we consider the atomic orbitals and their angles to each other (shown below), the bond angles in the VSEPR shapes seem to make no sense

- The angle between these orbitals is 90∘
- The atomic orbitals ψ represent solutions to the Schrödinger wave equation, which for hydrogen-like (one-electron) atoms can be written as Eψ=−ℏ22μ∇2ψ−Ze24πε0rψ
Schrödinger Wave Equation
Eψ=−ℏ22μ∇2ψ−Ze24πε0rψ
- Z is the nuclear charge
- e is the electron charge
- r is the position of the electron
- ε0 is the permittivity of free space
- μ=memnme+mn≈me is the reduced mass
Important Points About the Schrödinger Equation
Eψ=−ℏ22μ∇2ψ−Ze24πε0rψ
- The equation is a differential equation, in with the Laplacian operator ∇2 takes the second derivative (with respect to three spacial coordinates) of the wavefunction ψ
- The solution to the equation are a set of energies E and wavefunctions (atomic orbitals)
- Sometimes the energies are referred to as eigenvalues and the orbitals as eigenfunctions
- The E values and their associated wavefunctions are characterized according to their quantum numbers
Orbital Hybridization
- Add and subtract atomic orbitals to get hybrid orbitals
- We get the same number of orbitals out as we put in
- The energy of a hybrid orbital is the weighted average of the atomic orbitals that make it up
- The coefficients are determined by the constraints that the hybrid orbitals must be orthogonal and normalized
- orthogonal - the product of any two orthogonal wavefunctions is zero
- normalized - the integral of the wavefunction over all space is equal to one (unity, 100%)
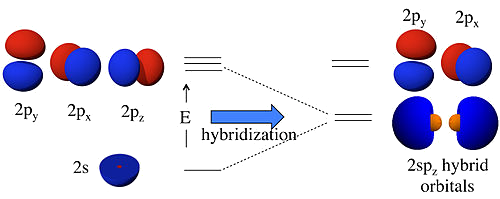
sp Hybridization
- sp hybridization is a linear combinations of the 2s and 2pz orbitals ψ1=1√2(2s)+1√2(2pz) and ψ2=1√2(2s)−1√2(2pz)
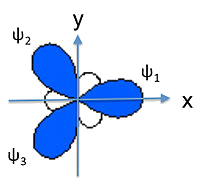
sp2 Hybridization
ψ1=1√3(2s)+√2√3(2px) ψ2=1√3(2s)−1√6(2px)+1√2(2py) ψ3=1√3(2s)−1√6(2px)−1√2(2py)
sp3 Hybridization
ψ1=12(2s+2px+2py+2pz) and ψ2=12(2s−2px−2py+2pz) ψ3=12(2s+2px−2py−2pz) and ψ4=12(2s−2px+2py−2pz)
Bond Polarity and Bond Strength
- The electronegativity of an atom, represented by χ, can be defined as the tendency of an atom to draw electrons to itself in a chemical bond
- On the Pauling scale, the electronegativity difference between two atoms A and B are defined in terms of the dissociation energies (Ed) of the A-A, B-B, and A-B bonds: χA−χB=√Ed(AB)−Ed(AA)−Ed(BB)2 where the energies are expressed in electron volts.
More on Electronegativity
- The previous definition of electronegativies is directly relevant to the strength of chemical bonds
- The difficulty in the definition is that it requires thermochemical input data from many compounds, some of which were not available during Pauling's lifetime
- The Mulliken scale of electronegativities is based on the average of the electron affinity and ionization energy of the free A and B atoms
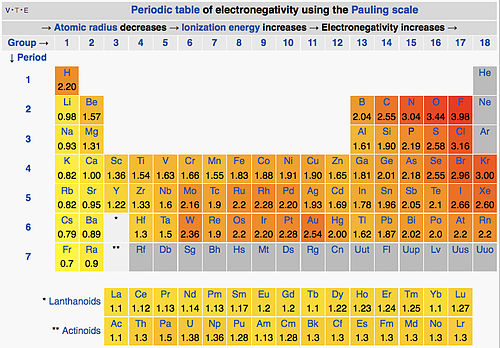
- On the Pauling scale, the least electronegative elements are the alkali metals (χ=0.7−1.0) and the most electronegative are oxygen (3.5) and fluorine (4.0)
Pauling Electronegativity Table
Bond Polarity
- The polarity of a bond is determined by electronegativity differences
- The following guidelines are used to determine polarity
- ionic if Δχ>2.0
- polar if 2.0>Δχ>0.5
- nonpolar if 0.5>Δχ
- Polarity helps us understand non-covalent forces between molecules
Polarity and Reactivities
- The Si-H bond (χSi=1.8, χH=2.1) is more hydride-like than the C-H bond (χC=2.5, χH=2.1).
- This means that silanes react with acids to make H2
- Phosphines (χP=2.1) and hydrocarbons do not react with acids to make H2
Strength vs Bond Length
- The longer the bond, the weaker it is because of weaker orbital overlap
- The empirical formula relating bond length to bond strength for a pair of atoms is D(n)=D(1)−0.6log10(n) where D(n) represents the bond length if Å and n is the bond order. D(1) is the length of a single bond.
1 / 49