Chapter 18

Representative Metals, Metalloids, and Nonmetals

Shaun Williams, PhD

Reviewing the Periodic Table Regions

Representative elements:

Groups 1A – 8A (filling s and p orbitals)

Transition metals:

Center of the table (filling d orbitals)

Lanthanides and Actinides:

Listed separately, on the bottom of the table (filling 4f and 5f orbitals)

Metalloids:

Separate metals from nonmetals

The Atomic Radii of Some Representative Elements (in Picometers)

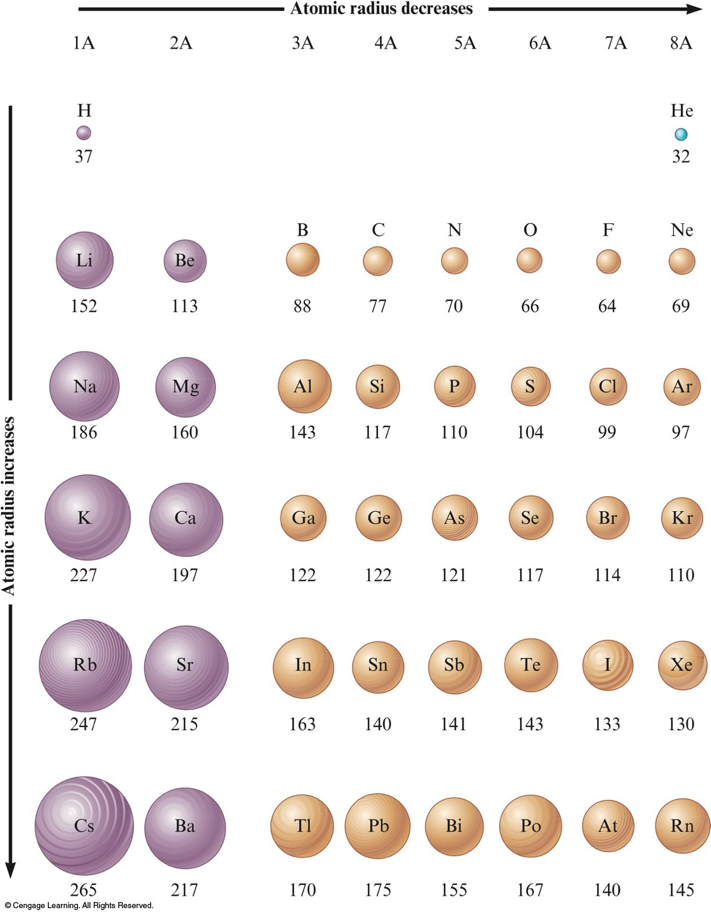
A basic table diagram showing the largest atom, cesium with a radius of 265 picometer, in the bottom left of the periodic table. The smallest atom, helium with a radius of 32 picometers, is in the upper right of the periodic table.

Concept Check

Which should be the larger atom, Na or Cl? Why?

Concept Check

Which should be the larger atom, Li or Cs? Why?

Distribution (Mass Percent) of the 18 Most Abundant Element on Earth

Element	Mass Percent	Element	Mass Percent
Oxygen	49.2	Chlorine	0.19
Silicon	25.7	Phosphorous	0.11
Aluminum	7.50	Manganese	0.09
Iron	4.71	Carbon	0.08
Calcium	3.39	Sulfur	0.06
Sodium	2.63	Barium	0.04
Potassium	2.40	Nitrogen	0.03
Magnesium	1.93	Fluorine	0.03
Hydrogen	0.87	All others	0.49
Titanium	0.58

Abundance of the Elements in the Human Body

Major Element	Mass Percent	Trace Elements (in alphabetical order)
Oxygen	65.0	Arsenic
Carbon	18.0	Chromium
Hydrogen	10.0	Cobalt
Nitrogen	3.0	Copper
Calcium	1.4	Fluorine
Phosphorus	1.0	Iodine
Magnesium	0.50	Manganese
Potassium	0.34	Molybdenum
Sulfur	0.26	Nickel
Sodium	0.14	Selenium
Chlorine	0.14	Silicon
Iron	0.004	Vanadium
Zinc	0.003

Alkali Metals: Sources and Methods of Preparation

Element	Source	Method of Preparation
Lithium	Silicate minerals such as spodumene, $\chem{LiAl(Si_2O_6)}$	Electrolysis of molten $\chem{LiCl}$
Sodium	$\chem{NaCl}$	Electrolysis of molten $\chem{NaCl}$
Potassium	$\chem{KCl}$	Electrolysis of molten $\chem{KCl}$
Rubidium	Impurity in lepidolite, $\chem{Li_2(F, OH)_2Al_2(SiO_3)_3}$	Reduction of $\chem{RbOH}$ with $\chem{Mg}$ and $\chem{H_2}$
Cesium	Pollucite( $\chem{Cs_4Al_4Si_9O_26\cdot H_2O}$ ) and an impurity if lepidolite	Reduction of $\chem{CsOH}$ with $\chem{Mg}$ and $\chem{H_2}$

Selected Reactions of the Alkali Metals

Reaction	Comment
$\chem{2M+X_2 \rightarrow 2MX}$	$\chem{X_2}$ is any halogen molecule
$\chem{4Li+O_2 \rightarrow 2Li_2O}$	Excess oxygen
$\chem{2Na+O_2 \rightarrow Na_2O_2}$
$\chem{M+O_2 \rightarrow MO_2}$	$\chem{M}$ is $\chem{K}$ , $\chem{Rb}$ , or $\chem{Cs}$
$\chem{2M+S \rightarrow M_2S}$
$\chem{6Li+N_2 \rightarrow 2Li_3N}$	$\chem{Li}$ only
$\chem{12M+P_4 \rightarrow 4M_3P}$
$\chem{2M+H_2 \rightarrow 2MH}$
$\chem{2M+2H_2O \rightarrow 2MOH+H_2}$
$\chem{2M+2H^+ \rightarrow 2M^++H_2}$	Violent reaction!

Exercise

Predict the products formed by the following reactants: $\chem{Na_2O_2(s)+H_2O(l)}$

Hydrides

Binary compounds containing hydrogen:

Ionic hydrides: hydrogen + the most active metals (eg; $\chem{LiH}$ , $\chem{CaH_2}$ )
Covalent hydrides: hydrogen + other nonmetals (eg; $\chem{H_2O}$ , $\chem{CH_4}$ , $\chem{NH_3}$ )
Metallic (interstitial) hydrides: transition metal crystals treated with $\chem{H_2}$ gas

Exercise

Predict the products formed by the following reactants: $\chem{LiH(s)+H_2O(l)}$

Alkaline Earth Metals

Very reactive
Great practical importance:

Human life ( $\chem{Ca}$ and $\chem{Mg}$ )

Selected Reactions of the Group 2A Elements

Reaction	Comment
$\chem{M+X_2 \rightarrow MX_2}$	$\chem{X_2}$ is any halogen molecule
$\chem{2M+O_2 \rightarrow 2MO}$	$\chem{Ba}$ gives $\chem{BaO_2}$ as well
$\chem{M+S \rightarrow MS}$
$\chem{3M+N_2 \rightarrow M_3N_2}$	High temperatures
$\chem{6M+P_4 \rightarrow 2M_3P_2}$	High temperatures
$\chem{M+H_2 \rightarrow MH_2}$	$\chem{M}$ is $\chem{Ca}$ , $\chem{Sr}$ , or $\chem{Ba}$ ; high temperatures; $\chem{Mg}$ at high pressure
$\chem{M+2H_2O \rightarrow M(OH)_2+H_2}$	$\chem{M}$ is $\chem{Ca}$ , $\chem{Sr}$ , or $\chem{Ba}$
$\chem{M+2H^+ \rightarrow M^{2+}+H_2}$
$\chem{Be+2OH^-+2H_2O \rightarrow Be(OH)_2^{2-}+H_2}$

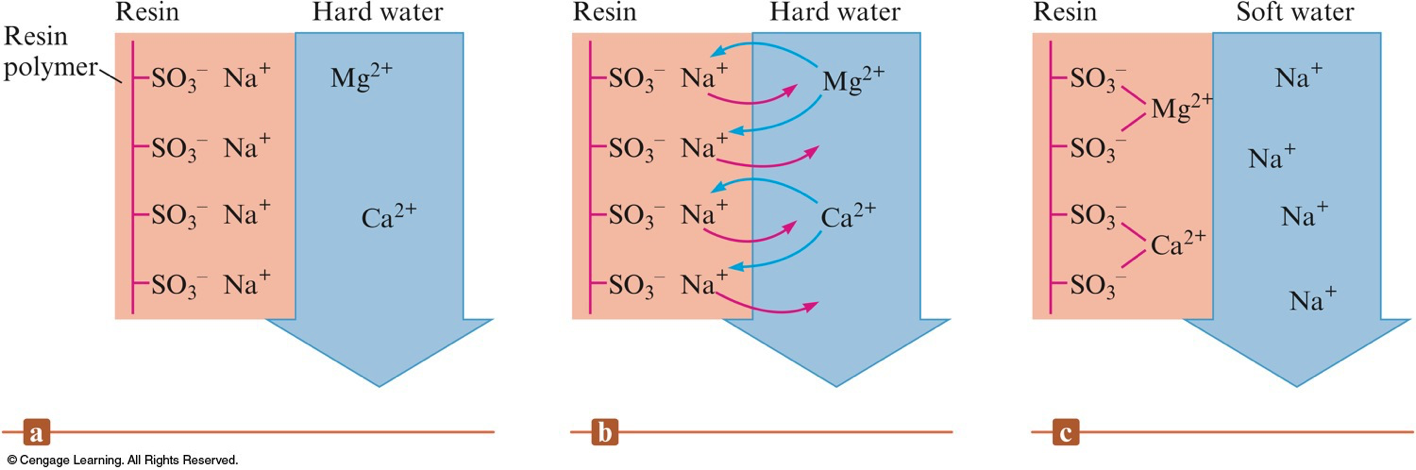
Ion Exchange

$\chem{Ca^{2+}}$ and $\chem{Mg^{2+}}$ are often removed during ion exchange, releasing $\chem{Na^+}$ into solution.
Ion exchange resin – large molecules that have many ionic sites.

A Schematic Representation of a Typcical Cation Exchange Resin

Hard water contains magnesium ions and calcium ions. The resin contains simply sodium ions. When the hard water is introduced to the resin, the magnesium ions and calcium ions replace the sodium ions in the resin, thereby getting stuck in the resin. The sodium ions are left in the water, which is now soft water.

Group 3A Elements

Group 3A elements generally show the increase in metallic character in going down the group that is characteristic of the representative elements.
$\chem{B}$ , $\chem{Al}$ , $\chem{Ga}$ , $\chem{In}$ , $\chem{Tl}$

Some Physical Properties, Sources, and Methods of Preparation of the Group 3A Elements

Element	Radius of $\chem{M^{3+}}$ (pm)	Ionization Energy (kJ/mol)	$\mathcal{E}^\circ\,(\mathrm{V})$ $\chem{M^{3+}+3e^-\rightarrow M}$	Source	Method of Preparation
Boron	20	798	-	Kernite, a form of borax ( $\chem{Na_2B_4O_7\cdot 4H_2O}$ )	Reduction by $\chem{Mg}$ or $\chem{H_2}$
Aluminum	50	581	-1.66	Bauxite ( $\chem{Al_2O_3}$ )	Electrolysis of $\chem{Al_2O_3}$ in molten $\chem{Na_3AlF_6}$
Gallium	62	577	-0.53	Traces in various minerals	Reduction with $\chem{H_2}$ or electrolysis
Indium	81	556	-0.34	Traces in various minerals	Reduction with $\chem{H_2}$ or electrolysis
Thallium	95	589	0.72	Traces in various minerals	Electrolysis

Selected Reactions of the Group 3A Elements

Reaction	Comment
$\chem{2M+3X_2 \rightarrow 2MX_3}$	$\chem{X_2}$ is any halogen molecule; $\chem{Tl}$ gives $\chem{TlX}$ as well, but no $\chem{TlI_3}$
$\chem{4M+3O_2 \rightarrow 2M_2O_3}$	High temperatures; $\chem{Tl}$ gives $\chem{Tl_2O}$ as well
$\chem{2M+3S \rightarrow M_2S_3}$	High temperatures; $\chem{Tl}$ gives $\chem{Tl_2S}$ as well
$\chem{2M+N_2 \rightarrow 2MN}$	$\chem{M}$ is $\chem{Al}$ only
$\chem{2M+6H^+ \rightarrow 2M^{3+}+3H_2}$	$\chem{M}$ is $\chem{Al}$ , $\chem{Ga}$ , or $\chem{In}$ ; $\chem{Tl}$ gives $\chem{Tl^+}$
$\chem{2M+2OH^-+6H_2O \rightarrow 2M(OH)_4^-+3H_2}$	$\chem{M}$ is $\chem{Al}$ or $\chem{Ga}$

Group 4A Elements

Contains two of the most important elements on earth: carbon and silicon.
Can form four covalent bonds to nonmetals.

$\chem{CH_4}$ , $\chem{SiF_4}$ , $\chem{GeBr_4}$

Some Physical Properties, Sources, and Methods of Preparation of the Group 4A Elements

Element	Electronegativity	Melting Point ( ${}^\circ \mathrm{C}$ )	Boiling Point ( ${}^\circ \mathrm{C}$ )	Source	Method of Preparation
Carbon	2.6	3727 (sublimes)	-	Graphite, diamond, petroleum, coal	-
Silicon	1.9	1410	2355	Silicate minerals, silica	Reduction of $\chem{K_2SiF_6}$ with $\chem{Al}$ , or reduction of $\chem{SiO_2}$ with $\chem{Mg}$
Germanium	2.0	937	2830	Germinate (mixture of copper, iron, and germanium sulfides)	Reduction of $\chem{GeO_2}$ with $\chem{H_2}$ or $\chem{C}$
Tin	2.0	327	2270	Cassiterite ( $\chem{SnO_2}$ )	Reduction of $\chem{SnO_2}$ with $\chem{C}$
Lead	2.3	327	1740	Galena ( $\chem{PbS}$ )	Reduction of $\chem{PbS}$ with $\chem{O_2}$ to form $\chem{PbO_2}$ and then reduction with $\chem{C}$

Selected Reactions of the Group 4A Elements

Reaction	Comment
$\chem{M+2X_2 \rightarrow MX_4}$	$\chem{X_2}$ is any halogen molecule; $\chem{M}$ is $\chem{Ge}$ or $\chem{Sn}$ ; $\chem{Pb}$ gives $\chem{PbX_2}$
$\chem{M+O_2 \rightarrow MO_2}$	$\chem{M}$ is $\chem{Ge}$ or $\chem{Sn}$ ; high temperatures; $\chem{Pb}$ gives $\chem{PbO}$ or $\chem{Pb_3O_4}$
$\chem{M+2H^+ \rightarrow M^{2+}+H_2}$	$\chem{M}$ is $\chem{Sn}$ or $\chem{Pb}$

Group 5A Elements

Exhibits varied chemical properties.
$\chem{N}$ , $\chem{P}$ , $\chem{As}$ , $\chem{Sb}$ , $\chem{Bi}$

Some Physical Properties, Sources, and Methods of Preparation of the Group 5A Elements

Element	Electronegativity	Source	Method of Preparation
Nitrogen	3.0	Air	Liquifaction of Air
Phosphorus	2.2	Phosphate rock ( $\chem{Ca_3(PO_4)_2}$ ), fluorapatite ( $\chem{Ca_5(PO_4)_3F}$ )	$\chem{2Ca_3(PO_4)_2+6SiO_2 \rightarrow 6CaSiO_3+P_4O_{10}}$ $\chem{P_4O_{10}+10C\rightarrow 4P+10CO}$
Arsenic	2.2	Arsenopyrite ( $\chem{Fe_3As_2}$ , $\chem{FeS}$ )	Heating arsenopyrite in the absence of air
Antimony	2.1	Stibnite ( $\chem{Sb_2S_3}$ )	Roasting $\chem{Sb_2S_3}$ in air to form $\chem{Sb_2O_3}$ and then reduction with carbon
Bismuth	2.0	Bismite ( $\chem{Bi_2O_3}$ ), bismuth glance ( $\chem{Bi_2S_3}$ )	Roasting $\chem{Bi_2S_3}$ in air to form $\chem{Bi_2O_3}$ and then reduction with carbon

Nitrogen

The great stability of the $\chem{N\equiv N}$ bond means that most binary compounds containing nitrogen decompose exothermically to the elements.

$\begin{align} \chem{NO_2(g)} \rightarrow & \chem{\frac{1}{2}N_2(g)+O_2(g)} \\ & \Delta H^\circ = -34\,\mathrm{kJ} \\ \chem{N_2H_4(a)} \rightarrow & \chem{N_2(g)+2H_2(g)} \\ & \Delta H^\circ = -95\,\mathrm{kJ} \end{align}$

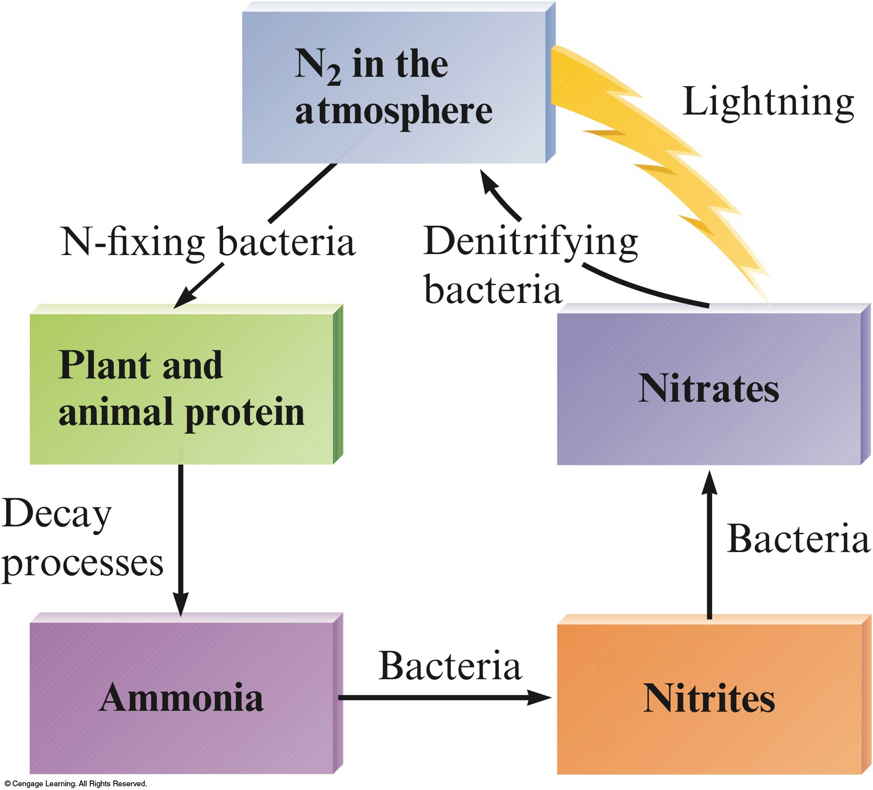
Nitrogen Fixation

The process of transforming N2 to other nitrogen–containing compounds.
The Haber Process:

$\begin{align} \chem{N_2(g)+3H_2(g)} \rightarrow & \chem{2NH_3(g)} \\ & \Delta H^\circ = -92\,\mathrm{kJ} \end{align}$

The Nitrogen Cycle

Nitrogen gas in the atmosphere is converted by nitrogen-fixing plants to plant and animal protein. This protein eventually decays to ammonia. Bacteria convert the ammonia to nitrites. Other bacteria convert the nitrites into nitrates. Denitrifying bacteria then convert the nirates into atmoshperic nitrogen.

Nitrogen Hydrides

Ammonia, $\chem{NH_3}$

Fertilizers

Hydrazine, $\chem{N_2H_4}$

Rocket propellant, manufacture of plastics, agricultural pesticides

Monomethylhydrazine, $\chem{N_2H_3(CH_3)}$

Rocket fuels

Nitrogen Oxides

Nitrogen in its oxides has oxidation states from +1 to +5.

In other compounds, nitrogen could have oxidation states of -1 to -3.

Compound	Oxidation State of $\chem{N}$
$\chem{N_2O}$	+1
$\chem{NO}$	+2
$\chem{N_2O_3}$	+3
$\chem{NO_2}$	+4
$\chem{HNO_3}$	+5

Nitrogen Oxyacids

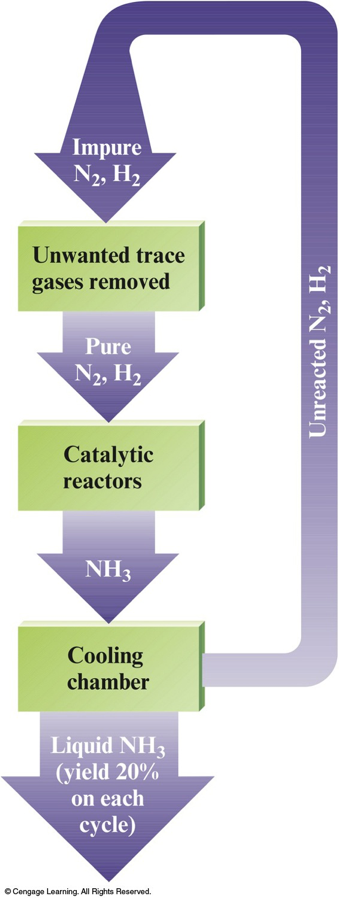
Nitric acid, $\chem{HNO_3}$

$\chem{4HNO_3(l)} \xrightarrow{h\nu} \chem{4NO_2(g)+2H_2O(l)+O_2(g)}$

Nitrous acid, $\chem{HNO_2}$

$\chem{HNO_2(aq) \rightleftharpoons H^+(aq)+NO_2^-(aq)}$

The Ostwald Process

Allotropes of Phosphorus

White Phosphorus = $\chem{P_4}$ (tetrahedral) - very reactive
Black Phosphorus = crystalline structure - much less reactive
Red Phosphorus = amorphous with $\chem{P_4}$ chains

$\begin{align} \chem{P(white)} & \xrightarrow{\text{heat, 1 atm, no air}} \chem{P(red)} \\ \chem{P(white)\;\mathrm{or}\;P(red)} & \xrightarrow{\text{high pressure}} \chem{P(black)} \\ \end{align}$

Allotropes of Phosphorus

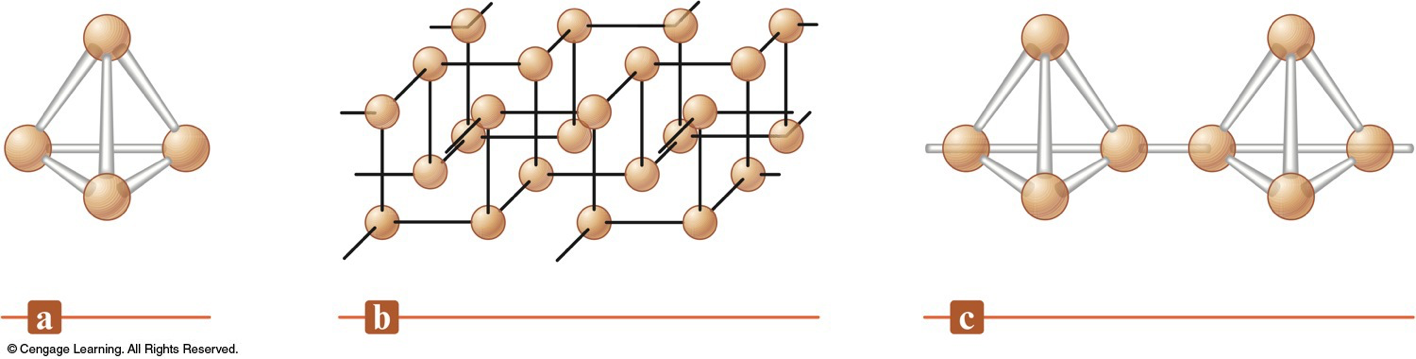
Comparison of the three crystal structures of phosphorus. Both white and red phosphorus have a tetrahedral arrangement of their atoms. Black phosphorus has a more square arrangement of the atoms.

$\chem{P_{white}}$
$\chem{P_{black}}$
$\chem{P_{red}}$

Phosphorus Oxyacids

Phosphoric acid, $\chem{H_3PO_4}$
Phosphorous acid, $\chem{H_3PO_3}$
Hypophosphorous acid, $\chem{H_3PO_2}$

The Group 6A Elements

$\chem{O}$ , $\chem{S}$ , $\chem{Se}$ , $\chem{Te}$ , $\chem{Po}$
Although in Group 6A there is the usual tendency for metallic properties to increase going down the group, none of the Group 6A elements behaves as a typical metal.
Can form covalent bonds with other nonmetals.

Some Physical Properties, Sources, and Methods of Preparation of the Group 6A Elements

Element	Electronegativity	Radius of $\chem{X^{2-}}$ (pm)	Source	Method of Preparation
Oxygen	3.4	140	Air	Distillaton from liquid air
Sulfur	2.6	184	Sulfur deposits	Melted with hot water and pumped to the surface
Selenium	2.6	198	Impurity in sulfide ores	Reduction of $\chem{H_2SeO_4}$ with $\chem{SO_2}$
Tellurium	2.1	221	Nagyagite (mixed sulfide and telluride)	Reduction of ore with $\chem{SO_3}$
Polonium	2.0	230	Pitchblende

Oxygen

$\chem{O_2}$ makes up 21% of the Earth’s atmosphere.
$\chem{O_3}$ (ozone) exists naturally in the upper atmosphere of the Earth.

Ozone layer absorbs UV light and acts as a screen to prevent this radiation from penetrating to the Earth’s surface.
Scientists have become concerned that Freons and nitrogen dioxide are promoting the destruction of the ozone layer.

Ozone

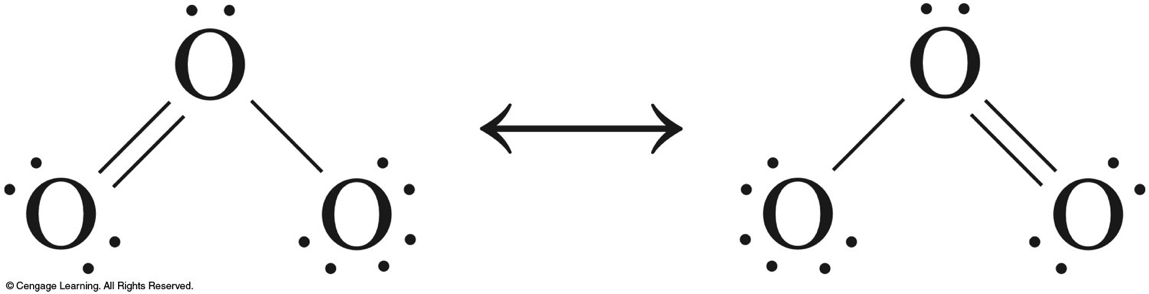
The two resonance structure of ozone. The structure flip the double bond between oxygen atoms numbered 1 and 2 versus atoms numbered 2 and 3.

$\begin{align} & \chem{3O_2(g) \rightleftharpoons 2O_3(g)\;\;\;\;K\approx 10^{-56}} \\ & \chem{O_3} \xrightarrow{h\nu} \chem{O_2+O} \end{align}$

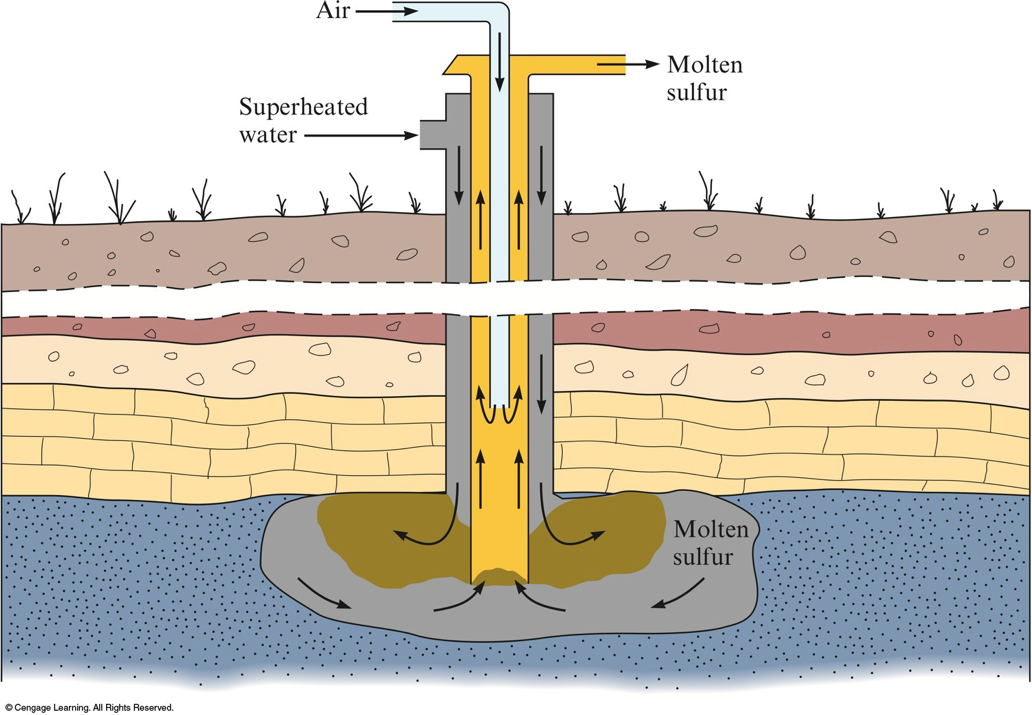
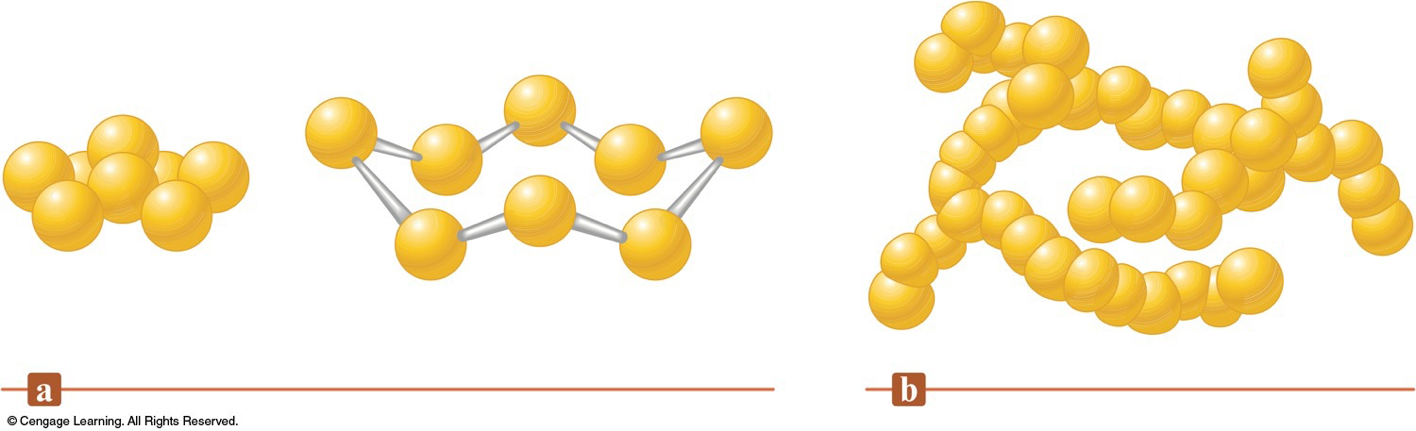
Sulfur

Sulfur is found in nature both in large deposits of the free element and in ores such as galena, cinnabar, pyrite, gypsum, epsomite, and glauberite.

Frasch Process

Superheated water and air is pumped underground into a deposit of sulfur. The sulfur melts and is pushed up and out of the group by the air.

Aggregates of Sulfur

Different structures of solid sulfur. Some sulfur exists as rings of eight sulfur atoms while other sulfur exists as random chains of sulfur atoms.

Sulfur Oxide Reactions

$\begin{align} \chem{2SO_2(g)+O_2(g)} & \rightarrow \chem{2SO_3(g)} \\ \chem{SO_2(g)+H_2O(l)} & \rightarrow \chem{H_2SO_3(aq)} \\ \chem{SO_3(g)+H_2O(l)} & \rightarrow \chem{H_2SO_4(aq)} \end{align}$

Halogens

All nonmetals: $\chem{F}$ , $\chem{Cl}$ , $\chem{Br}$ , $\chem{I}$ , $\chem{At}$
Because of their high reactivities, the halogens are not found as free elements in nature. They are found as halide ions ( $\chem{X^–}$ ) in various minerals and in seawater.

Trends in Selected Physical Properties of the Group 7A Elements

Element	Electronegativity	Radius of $\chem{X^-}$ (pm)	$\mathcal{E}^\circ$ (V) for $\chem{X_2+2e^- \rightarrow 2X^-}$	Bond Energy of $\chem{X_2}$ (kJ/mol)
Fluorine	4.0	136	2.87	154
Chlorine	3.2	181	1.36	239
Bromine	3.0	195	1.09	193
Iodine	2.7	216	0.54	149
Astatine	2.2	-	-	-

Some Physical Properties, Sources, and Methods of Preparation of the Group 7A Elements

Element	Color and State	Percentage of Earth's Crust	Metling Point ( ${}^\circ\mathrm{C}$ )	Boiling Point ( ${}^\circ\mathrm{C}$ )	Source	Method of Preparation
Fluorine	Pale yellow gas	0.07	-220	-188	Fluorospar ( $\chem{CaF_2}$ ), cryolite ( $\chem{Na_3AlF_6}$ ), fluorapatite ( $\chem{Ca_5(PO_4)_3F}$ )	Electrolysis of molten $\chem{KHF_2}$
Chlorine	Yellow-green gas	0.14	-101	-34	Rock salt ( $\chem{NaCl}$ ), halite ( $\chem{NaCl}$ ), sylvite ( $\chem{KCl}$ )	Electrolysis of aqueous $\chem{NaCl}$
Bromine	Red-brown liquid	$2.5 \times 10^{-4}$	-7.3	59	Seawater, brine wells	Oxidation of $\chem{Br^-}$ by $\chem{Cl_2}$
Iodine	Violet-black solid	$3 \times 10^{-5}$	113	184	Seaweed, brine wells	Oxidation of $\chem{I^-}$ by electrolysis or $\chem{MnO_2}$

Preparation of Hydrogen Halides

$\chem{H_2(g)+X_2(g)\rightarrow 2HX(g)}$

When dissolved in water, the hydrogen halides behave as acids, and all except hydrogen fluoride are completely dissociated.

Halogen Oxyacids and Oxyanions

All halogens except fluorine combine with various numbers of oxygen atoms to form a series of oxyacids.
The strengths of these acids vary in direct proportion to the number of oxygen atoms attached to the halogen, with the acid strength increasing as more oxygens are added.

The Known Oxyacids of the Halogens

Oxidation State of Halogen	Fluorine	Chlorine	Bromine	Iodine^*	General Name of Acids	General Name of Salts
+1	$\chem{HOF}$ ^†	$\chem{HOCl}$	$\chem{HOBr}$	$\chem{HOI}$	Hypohalous acid	Hypohalites, $\chem{MOX}$
+3	^‡	$\chem{HOClO}$	^‡	^‡	Halous acid	Halites, $\chem{MXO_2}$
+5	^‡	$\chem{HOClO_2}$	$\chem{HOBrO_2}$	$\chem{HOIO_2}$	Halic acid	Halates, $\chem{MXO_3}$
+7	^‡	$\chem{HOClO_3}$	$\chem{HOBrO_3}$	$\chem{HOIO_4}$	Perhalic acid	Perhalates, $\chem{MXO_4}$

^* Iodine also forms $\chem{H_4I_2O_9}$ (mesodiperiodic acid) and $\chem{H_5IO_6}$ (paraperiodic acid).

^† $\chem{HOF}$ oxidation state is best represented as -1.

^‡ Compound is unknown.

Noble Gases

Filled s and p valence orbitals
$\chem{He}$ and $\chem{Ne}$ form no compounds.
$\chem{Kr}$ and $\chem{Xe}$ have been observed to form chemical compounds:

$\begin{align} & \chem{Xe(g)+2F_2(g) \rightarrow XeF_4(s)}\;\;\;[\text{at 6 atm, }400^\circ\mathrm{C}] \\ & \chem{XeF_6(s)+3H_2O(l) \rightarrow XeO_3(aq)+6HF(aq)} \end{align}$

Selected Properties of Group 8A Elements

Element	Melting Point ( ${}^\circ\mathrm{C}$ )	Boiling Point ( ${}^\circ\mathrm{C}$ )	Atmoshperic Abundance (% by volume)	Example of Compounds
Helium	-270	-269	$5 \times 10^{-4}$	None
Neon	-249	-246	$1 \times 10^{-3}$	None
Argon	-189	-186	$9 \times 10^{-1}$	$\chem{HArF}$
Krypton	-157	-153	$1 \times 10^{-4}$	$\chem{KrF_2}$
Xenon	-112	-107	$9 \times 10^{-6}$	$\chem{XeF_4}$ , $\chem{XeO_3}$ , $\chem{XeF_6}$

Concept Check

Which of the following groups is the most reactive? Group 1A, Group 5A, Group 6A, or Group 8A?

Concept Check

White of the following groups does not contain at least one element that forms compounds with oxygen? Group 4A, Group 5A, Group 6A, Group 7A?

Chapter 18 Representative Metals, Metalloids, and Nonmetals

Chapter 18

Representative Metals, Metalloids, and Nonmetals