Rotational States
Shaun Williams, PhD
Introduction to Rotation
- Molecules can also rotate
- Transition between rotational energy levels are typically found in the far infrared and microwave regions of the EM spectrum
- A rotational spectrum of a simple diatomic molecule, \(\chem{{}^{12}C{}^{16}O}\) at \(40\, K\) is given below
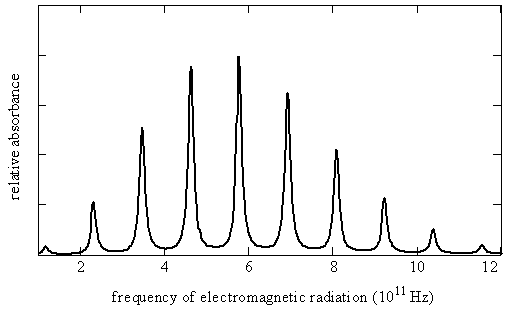
Brief Analysis of the Spectrum
- All the lines in the rotational spectrum are nearly equally spaced and vary in intensity
- We will see that the magnitude of the molecule's moment of inertia causes the rotational transitions to lie in these specific EM regions
- We will learn why the lines are nearly equally spaced
- We will learn why the lines vary in intensity
- These rotational spectra can be used to determine the bond lengths and bond angles in polyatomic molecules
- To develop our description of the rotational states, we will be considering the molecules to be a rigid object
- We will assume the bond lengths are fixed and the molecules cannot vibrate
- This model for rotation is called the rigid-rotor model
The Rotation of Rigid Objects
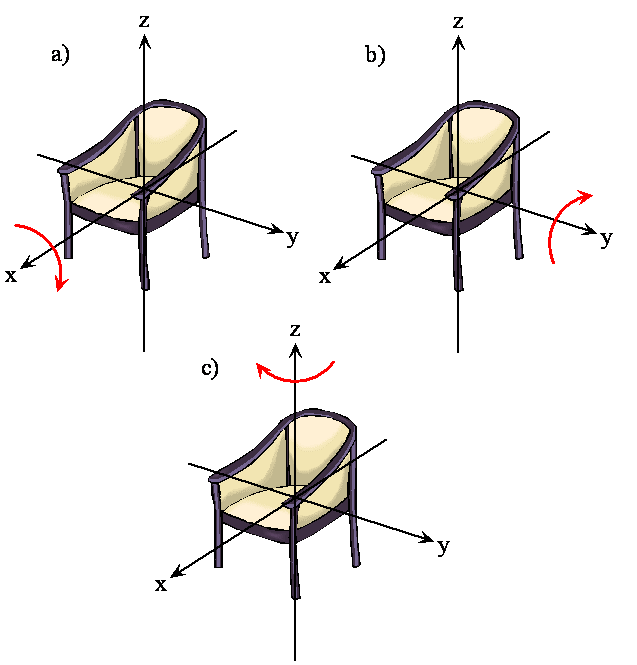
- Think about rotating any object
- There are orthogonal rotations about each of the three Cartesian coordinate axes
- This is the same as the three orthogonal translations
- The following two figures demonstrate these orthogonal rotations
Energy Quantization
- Like our other cases, we will find that the energy of rotation is also quantized
- This quantization and the selection rules for the transitions lead to the absorption lines seen previously
- Angular momentum is also quantized
- When a direction is uniquely defined by an electric or a magnetic field, only certain orientations of the rotating molecule are possible
- This restriction on orientation is called space quantization
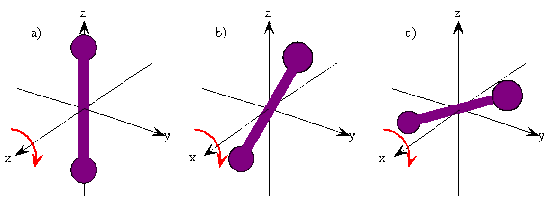
Angular Momentum
- As you can see above, the angular momentum vector for a classical rotating system is perpendicular to the plane of rotation
- The direction of the vector is given by applying the right-hand rule to the direction of rotation.
- The orientation of a classical rotating diatomic molecule is defined by the plane in which the internuclear axis lies during the rotation or by the direction of the angular momentum vector
More on Angular Momentum
- The direction of the angular momentum vector is called the axis-of-rotation
- Angular momentum vectors are useful because they provide a shorthand way to represent the classical motion of a rotating diatomic molecule
- It is possible to reconstruct the direction, plane of rotation, and the magnitude of the angular momentum using the angular momentum vector
- The magnitude of the angular momentum is a function of the reduced mass, bond length, and angular velocity of the rotating molecule
- The wavefunctions obtained for the rigid rotor will be used to describe the hydrogen atom which are key to understanding atomic and molecular structure
The Hamiltonian Operator for Rotational Motion
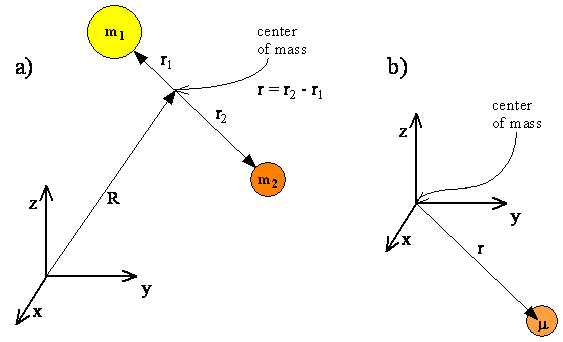
- Translational motion can be separated from rotational motion if we specify the position of the center of mass by a vector \( R\) and the positions of each atom relative to the center of mass by vectors \( r_1\) and \(r_2\)
- Since translational and rotational motion are separable, the translational and rotational energies will add and the total wavefunction will be a product of the translational and rotational functions.
Example 7.1
What do you need to know in order to write the Hamiltonian for the rigid rotor?
Beginning the Hamiltonian
- Let's start with the basic Hamiltonian: \( \hat{\mathcal{H}} = \hat{T}+\hat{V}\)
- Let's consider the classical energy of two rotating atoms
- In the classical rotating atoms, they are separated by a distance \(r\) can be treated as a single particle with reduced mass \(\mu\) at a distance \(r\) from the center of rotation (the center of mass)
- The kinetic energy of the reduced particle is $$ T=\frac{p^2}{2\mu} $$ where $$ p^2=p_x^2+p_y^2+p_z^2 $$
The Quantum Mechanical Kinetic Energy Operator
- We can now transform \(T\) into a quantum mechanical operator $$ \hat{T} = -\frac{\hbar^2 \nabla^2}{2\mu} $$ where \(\nabla^2\) is the Laplacian operator $$ \nabla^2 = \frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2} $$
- The rigid rotor model does not include the presence of electric or magnetic fields (or other external forces
- This means that \(\hat{V}=0\)
The Quantum Mechanical Hamiltonian
- Now, our quantum mechanical Hamiltonian operator is $$ \begin{equation} \hat{\mathcal{H}}=\hat{T}+\hat{V}=-\frac{\hbar^2 \nabla^2}{2\mu} \label{eq:7.2.7} \end{equation} $$
- Cartesian coordinates are not convenient for rotating bodies
- We need to utilize spherical coordinates \((r,\theta,\phi)\)

Spherical Coordinates
- In spherical coordinates, our variables have limits
- \( 0 \le r \lt \infty\)
- \( 0 \le \theta \lt \pi\)
- \( 0 \le \phi \lt 2\pi \)
- Spherical coordinates are better because they reflect the spherical nature of a rotating molecule
- This is akin to using Cartesian coordinates to locate the rooms in a building where hallways intersect at \(90^\circ\) with vertical elevators
The Spherical Hamiltonian
- We need to express \(\nabla^2\) in terms of \(r\), \(\theta\), and \(\phi\) $$ \begin{equation} \nabla^2 = \frac{1}{r^2} \left( \frac{\partial}{\partial r}r^2 \frac{\partial}{\partial r}+\frac{1}{\sin \theta} \frac{\partial}{\partial \theta} \sin \theta \frac{\partial}{\partial \theta} + \frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \phi^2} \right) \label{eq:7.2.8} \end{equation} $$
- The Hamiltonian operator is, therefore, $$ \begin{equation} \hat{\mathcal{H}} = -\frac{\hbar^2}{2\mu r^2} \left[ \frac{\partial}{\partial r}r^2 \frac{\partial}{\partial r}+\frac{1}{\sin \theta} \frac{\partial}{\partial \theta} \sin \theta \frac{\partial}{\partial \theta} + \frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \phi^2} \right] \label{eq:7.2.9} \end{equation} $$
- This looks a lot more complicated but it has the advantage of using variables that are separated
- This means that the Schrödinger equation can be written as a sum of terms each depending on only a single variable
Solving the Rigid Rotor Schrödinger Equation
- To solve the Schrödinger equation for the rigid rotor, we will separate the variables and form single-variable equation that can be solved independently
- Only two variables, \(\theta\) and \(\phi\) are required in the rigid rotor model because the bond length \(r\) is taken to be constant \(r_0\)
- We write the rigid rotor wavefunctions as $$ \begin{equation} \psi(\theta,\phi)=\Theta(\theta)\Phi(\phi) \label{eq:7.3.1} \end{equation} $$ and $$ \begin{equation} \hat{\mathcal{H}}\psi(\theta,\phi)=E\psi(\theta,\phi) \label{eq:7.3.2} \end{equation} $$
Starting to Solve the Schrödinger Equation
- Now we plug in our Hamiltonian into equation \eqref{eq:7.3.2} $$ \begin{equation} -\frac{\hbar^2}{2\mu r_0^2} \left[ \frac{\partial}{\partial r_0}r_0^2 \frac{\partial}{\partial r_0}+\frac{1}{\sin \theta} \frac{\partial}{\partial \theta} \sin \theta \frac{\partial}{\partial \theta} + \frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \phi^2} \right] \Theta(\theta)\Phi(\phi) = E\Theta(\theta)\Phi(\phi) \label{eq:7.3.3} \end{equation} $$
- Since \(r=r_0\) is constant and does not appear as a variable in the functions, the partial derivatives with respect to \(r\) are zero
- We can also substitute the moment of inertia, \(I=\mu r_0^2\), in the denominator on the left $$ \begin{equation} -\frac{\hbar^2}{2I} \left[ \frac{1}{\sin \theta} \frac{\partial}{\partial \theta} \sin \theta \frac{\partial}{\partial \theta} + \frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \phi^2} \right] \Theta(\theta)\Phi(\phi) = E\Theta(\theta)\Phi(\phi) \label{eq:7.3.4} \end{equation} $$
Separating Variables
- To begin, multiply each side by \( \frac{2I}{\hbar^2} \) and \( \frac{-\sin^2 \theta}{\Theta(\theta)\Phi(\phi)} \) $$ \begin{equation} \frac{1}{\Theta(\theta)\Phi(\phi)}\left[ \sin \theta \frac{\partial}{\partial \theta} \sin \theta \frac{\partial}{\partial \theta} + \frac{\partial^2}{\partial \phi^2} \right] \Theta(\theta)\Phi(\phi) = \frac{-2IE\sin^2 \theta}{\hbar^2} \label{eq:7.3.5}\end{equation} $$
- Let's simplify things by defining
$$ \begin{equation} \lambda = \frac{2IE}{\hbar^2} \label{eq:7.3.6} \end{equation} $$
- Note: \(\lambda\) is just a compound variable. It is
NOT a wavelength
- Note: \(\lambda\) is just a compound variable. It is
More on the Separation of Variables
- Using our new compound variable \(\lambda\),evaluating the partial derivative, and rearranging \eqref{eq:7.3.5} gives $$ \begin{equation} \begin{split} \frac{1}{\Theta(\theta)} & \left[ \sin \theta \frac{\partial}{\partial \theta} \left( \sin \theta \frac{\partial}{\partial \theta} \right) \Theta(\theta) + \left( \lambda \sin^2 \theta \right) \Theta(\theta) \right] \\ & = -\frac{1}{\Phi(\phi)} \frac{\partial^2}{\partial \phi^2}\Phi(\phi) \end{split} \label{eq:7.3.7} \end{equation} $$
Example 7.2
Carry out the steps leading from Equation \eqref{eq:7.3.5} to Equation \eqref{eq:7.3.7}. Keep in mind that, if \(y\) is not a function of \(x\), $$ \frac{dy}{dx}=y\frac{d}{dx} $$
Analysis of Our Equation
$$ \begin{equation} \begin{split} \frac{1}{\Theta(\theta)} & \left[ \sin \theta \frac{\partial}{\partial \theta} \left( \sin \theta \frac{\partial}{\partial \theta} \right) \Theta(\theta) + \left( \lambda \sin^2 \theta \right) \Theta(\theta) \right] \\ & = -\frac{1}{\Phi(\phi)} \frac{\partial^2}{\partial \phi^2}\Phi(\phi) \end{split} \end{equation} $$
- Our equation says that the function on the left, depending only on the variable \(\theta\) always equals the function on the right, depending only on the variable \(\phi\) for all values of \(\theta\) and \(\phi\)
- The only way this is possible is if both sides are equal to a constant
- Let's call this constant \(m^2\) (we will soon square root it)
The equations that we need to solve
- Separating our variables and doing some algebra brings us to two differential equations that we need to solve $$ \begin{equation} \sin \theta \frac{d}{d\theta} \left( \sin \theta \frac{d}{d\theta} \right) \Theta(\theta) + \left( \lambda \sin^2 \theta - m^2 \right)\Theta(\theta)=0 \label{eq:7.3.9} \end{equation} $$ and $$ \begin{equation} \frac{d^2}{d\phi^2}\Phi(\phi) + m^2 \Phi(\phi) =0 \label{eq:7.3.10} \end{equation} $$
- The partial derivatives have been replaced by total derivatives because only a single variable is in each equation
Example 7.3
Show how Equation \eqref{eq:7.3.9} and \eqref{eq:7.3.10} are obtained from Equation \eqref{eq:7.3.7}.
The \(\phi\) Solution
- The \(\phi\) equation is similar to the Schrödinger equation for the free particle
- So, we immediately know it's solution from the previous chapter $$ \begin{equation} \Phi_m(\phi) = Ne^{\pm im\phi} \label{eq:7.3.11} \end{equation} $$
- The normalization condition can be used to determine \(N\) $$ \begin{equation} \int_0^{2\pi} \Phi^*(\phi) \Phi(\phi) d\phi = 1 \label{eq:7.3.12} \end{equation} $$
Example 7.4
Substitute Equation \eqref{eq:7.3.11} into Equation \eqref{eq:7.3.10} to show that it is a solution to that differential equation.
Example 7.5
Use the normalization condition, Equation \eqref{eq:7.3.12} to show that $$ N=\left( 2\pi \right)^{-\frac{1}{2}} $$
Quantization
- The values of \(m\) are found by using a cyclic boundary condition
- The cyclic boundary condition means that since \(\phi\) and \(\phi+2\pi\) refer to the same point in three dimensional space then \(\Phi(\phi)=\Phi(\phi+2\pi)\) $$ \begin{align} e^{im\phi} &= e^{im(\phi+2\pi)} \\ &= e^{im\phi} e^{im2\pi} \\ 1 &= e^{im2\pi} \end{align} $$
- This final statement is only true when $$ \begin{equation} m=\cdots, -3,-2,-1,0,1,2,3,\cdots \label{eq:7.3.16} \end{equation} $$
- So, \(m\) can equal any positive or negative integer or zero
Example 7.6
Use Euler's Formula to show that \(e^{im2\pi}\) equals 1 for \(m\) equal to zero or any positive or negative integer.
Building Up Our Wavefunction
- Now we have the \(\Phi(\phi)\) function $$ \begin{align} & \Phi(\phi) = \left( 2\pi \right)^{-\frac{1}{2}} e^{\pm im\phi} \label{eq:7.3.17} \\ & \text{with }m=0,\pm 1,\pm 2, \cdots \label{7.3.18} \end{align} $$
- Finding the \(\Theta(\theta)\) functions that are solutions to Equation \eqref{eq:7.3.9} is more complicated
- Solutions are found to be a set of power series called Associated Legendre Functions
- this is a power series of trigonometric functions
- The \(\Theta(\theta)\) functions are shown in the table on the following slide
Spherical Harmonic Wavefunctions
| \(m\) | \(J\) | \(\Theta_J^m(\theta)\) | \(\Phi(\phi)\) | \(Y_J^m(\theta,\phi)\) |
|---|---|---|---|---|
| \( 0 \) | \( 0 \) | \(\frac{1}{\sqrt{2}}\) | \(\frac{1}{\sqrt{2\pi}}\) | \(\frac{1}{\sqrt{4\pi}}\) |
| \( 0 \) | \( 1 \) | \( \sqrt{\frac{3}{2}} \cos \theta \) | \( \frac{1}{\sqrt{2\pi}} \) | \( \sqrt{\frac{3}{4\pi}} \cos \theta \) |
| \( 1 \) | \( 1 \) | \( \sqrt{\frac{3}{4}} \sin \theta \) | \( \frac{1}{\sqrt{2\pi}} e^{i\phi} \) | \( \sqrt{\frac{3}{8\pi}} \sin \theta e^{i\phi} \) |
| \( -1 \) | \( 1 \) | \( \sqrt{\frac{3}{4}} \sin \theta \) | \( \frac{1}{\sqrt{2\pi}} e^{-i\phi} \) | \( \sqrt{\frac{3}{8\pi}} \sin \theta e^{-i\phi} \) |
| \( 0 \) | \( 2 \) | \( \sqrt{\frac{5}{8}} \left( 3 \cos^2 \theta -1 \right) \) | \( \frac{1}{\sqrt{2\pi}} \) | \( \sqrt{\frac{5}{16\pi}} \left( 3\cos^2 \theta -1 \right) \) |
| \( 1 \) | \( 2 \) | \( \sqrt{\frac{15}{4}} \sin\theta \cos\theta \) | \( \frac{1}{\sqrt{2\pi}} e^{i\phi} \) | \( \sqrt{\frac{15}{8\pi}} \sin\theta \cos \theta e^{i\phi} \) |
| \( -1 \) | \( 2 \) | \( \sqrt{\frac{15}{4}}\sin \theta \cos \theta \) | \( \frac{1}{\sqrt{2\pi}}e^{-i\phi} \) | \( \sqrt{\frac{15}{8\pi}} \sin\theta \cos\theta e^{-i\phi} \) |
| \( 2 \) | \( 2 \) | \( \sqrt{\frac{15}{16}}\sin^2 \theta \) | \( \frac{1}{\sqrt{2\pi}} e^{2i\phi} \) | \( \sqrt{\frac{15}{32\pi}}\sin^2\theta e^{2i\phi} \) |
| \( -2 \) | \( 2 \) | \( \sqrt{\frac{15}{16}} \sin^2\theta \) | \( \frac{1}{\sqrt{2\pi}}e^{-2i\phi} \) | \( \sqrt{\frac{15}{32\pi}}\sin^2\theta e^{-2i\phi} \) |
Further Requirements
- The solution to the \(\theta\)-equation requires that \(\lambda\) in Equation \eqref{eq:7.3.7} be given by $$ \begin{equation} \lambda=J(J+1) \label{eq:7.3.19} \end{equation} $$ where $$ \begin{equation} J \ge \left| m \right| \label{eq:7.3.20} \end{equation} $$
- So, \(J\) can be 0 or any positive integer greater than or equal to \(m\)
- The pair of \(J\) and \(m\) identify the rotational state and the wavefunction
- Since \(J\) controls the allowed values of \(m\), we note this by changing the \(m\) variable to \(m_J\)
The Energy
- Combining Equations \eqref{eq:7.3.6} and \eqref{eq:7.3.19} reveals that the energy is quantized $$ \begin{equation} E=\frac{\hbar^2 \lambda}{2I} = J(J+1)\frac{\hbar^2}{2I} \label{eq:7.3.21} \end{equation} $$
- For simplicity, we typically use energy units of \(\frac{\hbar^2}{2I}\)
- The lowest energy state has \(J=0\) and \(m_J=0\) which has an energy \(E_0\)
- There is only one state with this energy - one set of quantum numbers, one wavefunction, and one set of properties
Example 7.7
Compute the energy levels for a rotating molecule for \(J=0\) to \(J=5\) using units of \(\frac{\hbar^2}{2I}\).
Higher Energy Levels
- The next energy level is \(J=1\) with energy \(\frac{2\hbar^2}{2I}\)
- Three states have this energy because \(m_J=+1,0,-1\)
- These different states correspond to different orientations of the rotating molecules in space
- States with the same energy are said to be degenerate
- The degeneracy of an energy level is the number of states with that energy
- The degeneracy of the \(J=1\) energy level is 3
- The next energy level is \(J=2\) with \(E=\frac{6\hbar^2}{2I}\) with a degeneracy of 5
- The degeneracy of a rigid rotator is always \(2J+1\)
Example 7.8
For \(J=0\) to \(J=5\), identify the degeneracy of each energy level and the values of the \(m_J\) quantum number that go with each value of the \(J\) quantum number. Construct a rotational energy level diagram including \(J = 0\) through \(5\). Label each level with the appropriate values for the quantum numbers \(J\) and \(m_J\). Describe how the spacing between levels varies with increasing \(J\).
Rigid Rotor Wavefunction
- A rigid rotor wavefunction can be written as single function \(Y(\theta,\phi)\) which is called a spherical harmonic function $$ \begin{equation} Y_J^{m_J}(\theta,\phi)=\Theta_J^{\left|m_J\right|}(\theta)\Phi_{m_J}(\phi) \label{eq:7.3.22} \end{equation} $$
- The spherical harmonic wavefunctions depends on both \(m_J\) and \(J\)
- The following slide provides plots of some of the \(\theta\) functions
Spherical Harmonics \(\theta\)-Functions
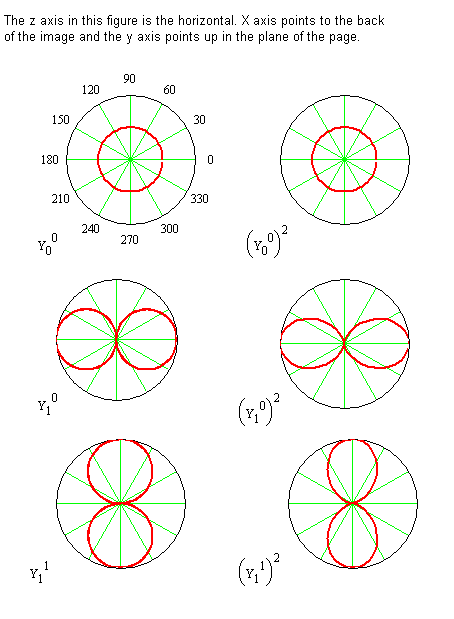 Polar plots in which the distance from the center gives the value of the function \(Y\) for the indicated angle \(\theta\).
Polar plots in which the distance from the center gives the value of the function \(Y\) for the indicated angle \(\theta\).
Two-Dimensional Space for a Rigid Rotor
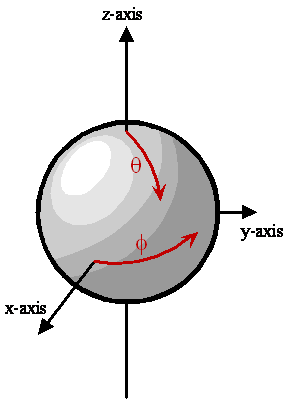 Space for a rigid rotor is restricted to the surface of a sphere of radius \(r_0\). The only degrees of freedom are motions along \(\theta\) or \(\phi\) on the surface of the sphere.
Space for a rigid rotor is restricted to the surface of a sphere of radius \(r_0\). The only degrees of freedom are motions along \(\theta\) or \(\phi\) on the surface of the sphere.
Rigid Rotor Probability
- The probability of finding the internuclear axis at specific coordinates \(\theta_0\) and \(\phi_0\) within an infinitesimal area \(ds\) is $$ \begin{equation} Pr\left[\theta_0,\phi_0\right] = Y_J^{m_J*}(\theta_0,\phi_0)Y_J^{m_J}(\theta_0,\phi_0)ds \label{eq:7.3.23} \end{equation} $$
- The area element \(ds\) is centered at \(\theta_0\) and \(\phi_0\)
- The absolute square (or modulus squared) of \(Y_J^{m_J*}(\theta,\phi)Y_J^{m_J}(\theta,\phi)\) gives the probability density for finding the internuclear axis oriented at \(\theta\) to the z-axis and \(\phi\) to the x-axis
- In spherical coordinates, the area element used for integrating \(\theta\) and \(\phi\) is $$ \begin{equation} ds = \sin \theta d\theta d\phi \label{eq:7.3.24} \end{equation} $$
Example 7.9
Use calculus to evaluate the probability of finding the internuclear axis of a molecule described by the \(J=1\), \(m_J=0\) wavefunction somewhere in the region defined by a range in \(\theta\) of \(0^\circ\) to \(45^\circ\), and a range in \(\phi\) of \(0^\circ\) to \(90^\circ\). Note that a double integral will be needed.
Looking At One Case
- Let's look at $$ \begin{equation} Y_1^0=\left(\frac{3}{4\pi}\right)^\frac{1}{2} \cos \theta \label{eq:7.3.25} \end{equation} $$
- The probability of finding the internuclear axis is independent of the angle \(\phi\) from the x-axis
- So the internuclear axis can be found in any plane containing the z-axis with equal probability
- The probability is greatest for finding the internuclear axis along the z-axis but there is a non-zero probability of find it at other values of \(\theta\)
- So the internuclear axis is not always aligned with the z-axis but it is most often
- The function is zero when \(\theta=90^\circ\)
- The entire xy-plane is a node
Example 7.10
For each state with \(J=0\) and \(J=1\), use the function form of the \(Y\) spherical harmonics and the figure several slides ago to determine the most probable orientation of the internuclear axis in a diatomic molecule, i.e. the most probable values for \(\theta\) and \(\phi\).
Angular Momentum Operator and Eigenvalues
- Angular momentum is a key component in the physical description of rotating systems
- It is important because just like energy and linear momentum, angular momentum must be conserved.
- Angular momentum is used to derive selection rues for spectroscopic transitions, determine which states of atoms and molecules can be affected by various perturbations, and identify possible and forbidden mechanisms in chemical reactions
- Rotational angular momentum explains the splitting of spectral lines and the angular distributions of gas-phase reaction products
How do we find the angular momentum?
- We now need the angular momentum operators that enable use to extract the angular momentum properties from the wavefunctions
- We are going to develop the operators for the total angular momentum and the z-component of angular momentum
- Since the energy of a rotating object is related to its total angular momentum \(M\) and moment of inertia \(I\) $$ \begin{equation} M^2 = 2IE \label{eq:7.4.1} \end{equation} $$
- Since the energy is quantized as we have seen, the total angular momentum is also quantized $$ \begin{equation} M^2 = J(J+1)\hbar^2 \label{eq:7.4.2} \end{equation} $$
- \(J\) is called the rotational angular momentum quantum number
Another Operator
- Just as there is an operator for the energy, \(\hat{\mathcal{H}}\), there is also an operator for the square of the angular momentum
- We can start with modifying Equation \eqref{eq:7.3.4} $$ \begin{equation} -\frac{\hbar^2}{2I} \left[ \frac{1}{\sin \theta}\frac{\partial}{\partial \theta} \sin \theta \frac{\partial}{\partial \theta} + \frac{1}{\sin^2 \theta} \frac{\partial^2}{\partial \phi^2} \right] Y_J^{m_J}(\theta,\phi)=EY_J^{m_J}(\theta,\phi) \label{eq:7.4.3} \end{equation} $$
- Multiplying both sides by \(2I\) and then using \(2IE=M^2\) gives $$ \begin{equation} -\hbar^2 \left[ \frac{1}{\sin \theta} \frac{\partial}{\partial \theta} \sin \theta \frac{\partial}{\partial \theta} + \frac{1}{\sin^2 \theta} \frac{\partial^2}{\partial \phi^2} \right] Y(\theta,\phi)=M^2Y(\theta,\phi) \label{eq:7.4.4} \end{equation} $$
- This is an eigenvalue equation: the operator on the left operates on the spherical harmonic function to give a value for \(M^2\)
The Square of the Angular Momentum Operator
- We have now found the operator for the square of the angular momentum $$ \begin{equation} \hat{M}^2 = -\hbar^2 \left[ \frac{1}{\sin \theta} \frac{\partial}{\partial \theta} \sin \theta \frac{\partial}{\partial \theta} + \frac{1}{\sin^2 \theta} \frac{\partial^2}{\partial \phi^2} \right] \label{eq:7.4.5} \end{equation} $$
- The spherical harmonics are eigenfunctions of \(\hat{M}^2\) with eigenvalues given by Equation \eqref{eq:7.4.2}
- The magnitude of the angular momentum, \(\sqrt{M^2}\) varies with the quantum number \(J\)
- The classical interpretation is that the molecule rotates with higher angular velocity in a state with higher \(J\) since neither the mass nor the radius of rotation can change
Z-Axis Angular Momentum
- The \(m_J\) quantum number is associated with the \(\phi\)-equation
- The \(m_J\) quantum number, therefore, describes rotation about the z-axis
- This implies that the \(m_J\) quantum number is related to the z-component of angular momentum
- To prove this, we need an operator for the z-component of angular momentum
- When we operator on the \(\Phi\) function with this operator we expect to get an eigenvalue for the z-component of angular momentum
- We can start by looking at the classical expression for the z-component of angular momentum $$ \begin{equation} M_z=xp_y - yp_x \label{eq:7.4.6} \end{equation} $$ $$ \begin{equation} \hat{M}_z = -i\hbar \left( x\frac{\partial}{\partial y} - y \frac{\partial}{\partial x} \right) \label{eq:7.4.7} \end{equation} $$
In spherical coordinates?
- We need to shift our z-component of angular momentum to spherical coordinates $$ \begin{equation} \hat{M}_z = -i\hbar \frac{\partial}{\partial \phi} \label{eq:7.4.8} \end{equation} $$
- In the following example you will prove that $$ \begin{equation} M_z=m_J \hbar \label{eq:7.4.10} \end{equation} $$
- The z-component of the angular momentum is very useful because it provides information about the orientation of the total angular momentum vector, \(M\)
- We can determine the magnitude of the total angular momentum from \(M^2\) but it is through \(M_z\) that we can determine the orientation of \(M\)
Example 7.11
Use the operator \(\hat{M}_z\) to operate on the general form of the wavefunction \(\Phi_m(\phi)\). Based on your result, what are the possible values for the z-component of the angular momentum?
Example 7.12
Determine the lengths of the angular momentum vectors, \(M\), for \(J=0\), \(1\), and \(2\) and the lengths of their projections on the z-axis.
What about \(M_x\) and \(M_y\)?
- In classical mechanics we could also find the x and y-components of the angular momentum
- In order for the rigid rotor wavefunctions to be eigenfunctions of \(\hat{M}_x\) and \(\hat{M}_y\) as well as \(\hat{M}_z\), these operators must commute with \(\hat{M}_z\) - they don't!
- Therefore, since the rigid rotor wavefunctions are not eigenfunctions of \(\hat{M}_x\) and \(\hat{M}_y\), we cannot obtain their eigenvalues
- This means that we cannot know anything about the x and y components of angular momentum
- This limitation is a manifestation of the Heisenberg Uncertainty Principle
- Since we know \(M_z\) exactly, we can have no knowledge of \(M_x\) and \(M_y\)
- Thus the angular momentum can be pointing with equal probability anywhere on a circle around the z-axis
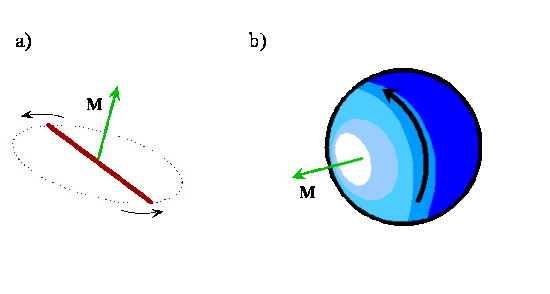
Three Possible Orientations of Angular Momentum
 The three possible orientations of the angular momentum vector \(M\) relative to the z axis for the \(J = 1\) states. a) \(m_J=1\), b) \(m_J=0\) and c) \(m_J=−1\). The lengths of the vectors are determined by \(M\) and the orientation angle is discussed later. The end of the \(M\) vector can lie at any point on the circle perpendicular to the z axis.
The three possible orientations of the angular momentum vector \(M\) relative to the z axis for the \(J = 1\) states. a) \(m_J=1\), b) \(m_J=0\) and c) \(m_J=−1\). The lengths of the vectors are determined by \(M\) and the orientation angle is discussed later. The end of the \(M\) vector can lie at any point on the circle perpendicular to the z axis.
Angles
- We now need to determine the angle between the total angular momentum and the z-axis
- We can do this using a little trigonometry
- It turns out from inspecting the graphs previous that $$ \begin{equation} \cos \alpha = \frac{m_J \hbar}{\sqrt{J(J+1)\hbar^2}} \label{eq:7.4.11} \end{equation} $$
- This means that $$ \begin{equation} \alpha=\cos^{-1}\left[ \frac{m_J}{\sqrt{J(J+1)}} \right] \label{eq:7.4.12} \end{equation} $$
Example 7.13
Calculate the possible angles a \(J=1\) angular momentum vector can have with respect to the z-axis.
Quantum Mechanical Properties of Rotating Diatomic Molecules
- In isotropic space (all directions are equivalent) any given molecule can have any orientation
- Without being able to distinguish directions, any molecule can point anywhere
- This means that there is not practical consequence of the \(m_J\) levels in isotropic space
- We can make space anisotropic by applying an external field (electric or magnetic)
Anisotropic Space
- With an external field, there become a unique direction in space and it is most convenient to assign that direction to the z-axis
- The effects of external electric and magnetic fields on atomic and molecular spectra is an active area of research
- For example, magnetic field effects on atomic spectra contributed to the discovery of electron spin
- These effects are known as Stark effects (electric fields) and Zeeman effects (magnetic fields)
The Ground Rotational State
- When \(J=0\), the rotational energy and angular momentum is zero
- With no rotational energy or angular momentum the molecule cannot be rotating
- The molecule may still be vibrating and translating however
- All values of \(\theta\) and \(\phi\) are equally probable so we have no information about the orientation of the molecule in this state
- Since there is no uncertainty in the angular momentum (it is exactly zero), having no information about the orientation (uncertainty is infinite) is consistent with the Heisenberg Uncertainty Principle
The First Excited State
- Now let's consider \(J=1\) with \(m_J=+1,0,-1\)
- The length of the angular momentum vector for all these states is \(\sqrt{2}\hbar\)
- The projections of this vector onto the z-axis are \(\hbar\), \(0\), and \(-\hbar\)
- The classical interpretation is that while the plane of rotation of the molecule is confined to a specific orientation with respect to the z-axis, it is not confined with respect to the x- and y- axes
The Classical Interpretation of the First Excited States

- The rotational state \((J,m_J)=(1,0)\)
- The angular momentum vector \(M\) is always perpendicular to the z-axis
The Other Two Cases
- For \(J=1\), \(m_J=1\) and \(m_J=-1\), the wavefunctions are given by $$ \begin{align} Y_1^1 &= \sqrt{\frac{3}{8\pi}} \sin \theta e^{i\phi} \label{eq:7.5.1} \\ Y_1^{-1} &= \sqrt{\frac{3}{8\pi}} \sin \theta e^{-i\phi} \label{eq:7.5.2} \end{align} $$
- The imaginary components are a bit confusing until we realize that it is the modulus squared that has physical interpretation as probability density $$ \begin{equation} \left| Y_1^1 \right|^2 = \left| Y_1^{-1} \right|^2 = \frac{3}{8\pi} \sin^2\theta \label{eq:7.5.3} \end{equation} $$
- Again, \(\phi\) does not appear in these equations
Analysis of these states
- We now know that there is no constraints on the wavefunction with respect to the angle \(\phi\) in these two states
- The \(\theta\) dependence is a \(\sin^2\) function, which has a maximum at \(90^\circ\) and goes to \(0\) as \(\theta\) goes to \(0^\circ\) and \(180^\circ\)
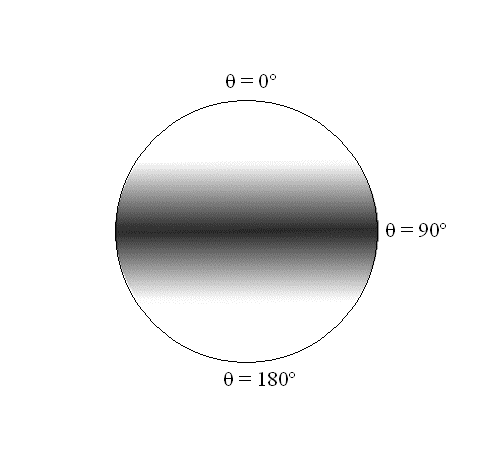 A map of the probability density associated with the \(Y_1^1\) and \(Y_1^{−1}\) spherical harmonics, mapped onto a sphere. The intensity of color is proportional to the probability density.
A map of the probability density associated with the \(Y_1^1\) and \(Y_1^{−1}\) spherical harmonics, mapped onto a sphere. The intensity of color is proportional to the probability density.
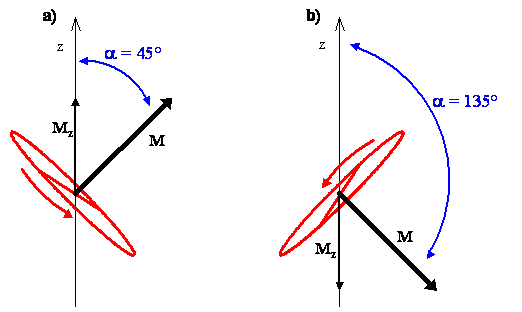
The Classical Interpretation of \(m_J=+1,-1\)
- We classically interpret these states as rotations which are tilted at an angle of \(45^\circ\) from the z-axis
- For \(m_J=-1\), the angular momentum vector is at an angle of \(\alpha=135^\circ\) from the z-axis
- This all means that, looking from above and using the right hand rule, the direction of rotation is clockwise for \(m_J=-1\) state and counterclockwise for the \(m_J=1\) state
Example 7.14
Five states have \(J=2\). Calculate the angles the angular momentum vectors for these states make with respect to the z-axis.
Rotational Spectroscopy of Diatomic Molecules
- The permanent electric dipole moments of polar molecules can couple to the electric field of EM radiation
- This coupling induces transitions between rotational states
- The energies of these transitions are detected in the far infrared and microwave regions
Beginning to Find Selection Rules
- The selection rules for the rotational transitions are derived from the transition moment integral using the dipole moment operator, \(\hat{\mu}\) $$ \begin{equation} \mu_T = \int Y_{J_f}^{m_f*} \hat{\mu} Y_{J_i}^{m_i} \sin \theta d\theta d\phi \label{eq:7.6.1} \end{equation} $$
- Evaluation reveals that the solution depends on the square of the dipole moment of the molecule and the initial rotational quantum number $$ \begin{equation} \mu_T = \mu^2 \frac{J+1}{2J+1} \label{eq:7.6.2} \end{equation} $$ and that the selection rules for rotational transitions are $$ \begin{equation} \Delta J=\pm 1 \label{eq:7.6.3} \end{equation} $$ $$ \begin{equation} \Delta m_J = 0,\pm 1 \label{eq:7.6.4} \end{equation} $$
Transition Energies
- The energies of the rotational levels are $$ \begin{equation} E=J(J+1)\frac{\hbar^2}{2I} \label{eq:7.6.5} \end{equation} $$
- The transition energies for absorption $$ \begin{equation} \Delta E_{states} = E_f-E_i = E_{photon} = h\nu = hc\widetilde{\nu} \label{eq:7.6.6} \end{equation} $$ $$ \begin{equation} h\nu = hc\widetilde{\nu} = J_f (J_f+1) \frac{\hbar^2}{2I} - J_i (J_i+1)\frac{\hbar^2}{2I} \label{eq:7.6.7} \end{equation} $$
- Due to the selection rule for absorption, \(J_f=J_i+1\) (\(\Delta J=+1\)) $$ \begin{equation} h\nu = hc\widetilde{\nu} = 2(J_i+1)\frac{\hbar^2}{2I} \label{eq:7.6.8} \end{equation} $$
More on the Transitions
- Solving our previous equation we can find the transition frequencies $$ \begin{equation} \nu = 2B(J_i+1) \label{eq:7.6.9} \end{equation} $$ where \(B\), the rotational constant of the molecule, is $$ \begin{equation} B=\frac{\hbar}{4\pi I} \label{eq:7.6.10} \end{equation} $$
- Note that this equation predicts that the transitions are equally spaced
Example 7.15
Complete the steps going from Equation \eqref{eq:7.6.7} to Equation \eqref{eq:7.6.10} and identify the units of \(B\) at the end.
Rotational Transitions in \(\chem{{}^{12}C{}^{16}O}\) at \(40\,K\)
| \(J\) | \(\nu_J\) (MHz) | Spacing from previous line (MHz) | \(\gamma_{max}\) |
|---|---|---|---|
| 0 | 115271.21 | 0 | 0.0082 |
| 1 | 230538.01 | 115266.80 | 0.0533 |
| 2 | 345795.99 | 115257.99 | 0.1278 |
| 3 | 461040.76 | 115244.77 | 0.1878 |
| 4 | 576267.91 | 115227.15 | 0.1983 |
| 5 | 691473.03 | 115205.12 | 0.1618 |
| 6 | 806651.78 | 115178.68 | 0.1064 |
| 7 | 921799.55 | 115147.84 | 0.0576 |
| 8 | 1036912.14 | 115112.59 | 0.0262 |
| 9 | 1151985.08 | 115072.94 | 0.0103 |
Non-Rigid Rotor Effects
- Centrifugal stretching of the bond as \(J\) increases causes the decrease in spacing between the lines in the observed spectrum
- This decrease shows that the molecule is not really a rigid rotor
- Basically as the rotational angular momentum increases the bond stretches
- This stretching increases the moment of inertia and decreases the rotational constant
More on Centrifugal Stretching
- The effect of centrifugal stretching is smallest at low \(J\) values
- This means that a good estimate for \(B\) can be obtained from the \(J=0\) to \(J=1\) transition
- From \(B\), a value for the bond length of the molecule can be obtained since the moment of inertia is in \(B\) (Equation \eqref{eq:7.6.10})
- When the centrifugal stretching is taken into account quantitatively, a very accurate and precise value for \(B\) can be obtained (this is beyond the scope of this class)
Example 7.16
Use the frequency of the \(J=0\) to \(J=1\) transition observed for carbon monoxide to determine a bond length for carbon monoxide.
Line Intensities
- The line intensities in a rotational spectrum do not all have the same intensity
- The maximum absorption coefficient for each line, \(\gamma_{max}\), is proportional to the magnitude of the transition moment, \(\mu_T\) (Equation \eqref{eq:7.6.2}), and to the population difference between the initial and final states, \(\Delta n\)
- Since \(\Delta n\) is the difference in the number of molecules present in the two states per unit volume, it is actually a difference in number density $$ \begin{equation} \gamma_{max} = C_{\mu T} \cdot \Delta n \label{eq:7.6.11} \end{equation} $$ where \(C\) includes constants obtained from a more complex derivation of the interaction of radiation with matter
Types of EM Interactions
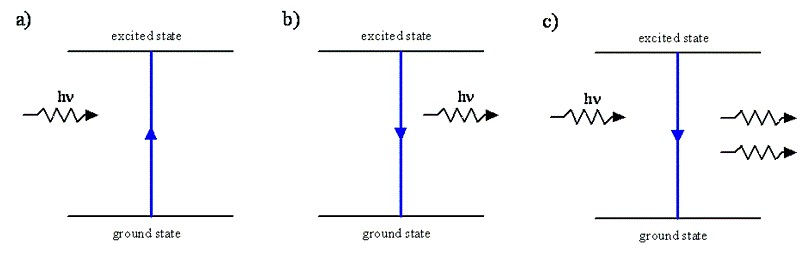
- In absorption, an incident photon is absorbed by the system and drives the system from a low energy state to a higher energy state
- In spontaneous emission, a photon is produced when a system goes from an excited state to a lower energy state
- In stimulate emissions, an incident photon is not absorbed but it drives the system from an exciting state to a lower energy state which is accompanied by the release of the second photon
State Populations
- Regardless of types, the observed interaction with EM radiation depends on the population difference, \(\Delta n\), between the states involved: \(\Delta n = n_J-n_{J+1}\)
- If \(\Delta n=0\), there will be no net effect. If \(\Delta n \gt 0\), absorption will be observed. If \(\Delta n \lt 0\), stimulated emission will be observed
- We can develop an expression that involves the Boltzmann factor
- We can first say that $$ \begin{equation} \Delta n = \left( 1-\frac{n_{J+1}}{n_J} \right)n_J \label{eq:7.6.13} \end{equation} $$
- The ratio of state populations is given by the Boltzmann factor $$ \begin{equation} \Delta n = \left( 1-e^{\frac{-h\nu_J}{k_BT}} \right) n_J \label{eq:7.6.14} \end{equation} $$
Our \(\Delta n\) Equation
- In Equation \eqref{eq:7.6.14}, \(h\nu_J\) is the energy difference between the two states
- For the rigid rotor $$ \begin{equation} \nu_j = 2B(J+1) \label{eq:7.6.15} \end{equation} $$ $$ \begin{equation} \Delta n = \left( 1 - e^{\frac{-2hB(J+1)}{k_BT}} \right)n_J \label{eq:7.6.16} \end{equation} $$
- To get the number density of molecules present in the initial state, \( n_J=F_J \cdot n_{total}\) where $$ \begin{equation} F_J = (2J+1)\left( \frac{hB}{k_BT} \right) \left( e^{\frac{-2hB(J+1)}{k_BT}} \right) \label{eq:7.6.18} \end{equation} $$
Back to Line Intensities
- Plugging things in $$ \begin{equation} \gamma_{max} = C \left( \mu^2 \frac{J+1}{2J+1} \right)\cdot \Delta n \label{eq:7.6.19} \end{equation} $$ $$ \begin{equation} \gamma_{max} = C \left( \mu^2 \frac{J+1}{2J+1} \right) \left( e^{\frac{-2hB(J+1)}{k_BT}} \right)n_J \label{eq:7.6.20} \end{equation} $$ $$ \begin{equation} \gamma_{max} = C \left( \mu^2 \frac{J+1}{2J+1} \right) \left( e^{\frac{-2hB(J+1)}{k_BT}} \right)\left[ (2J+1)\left( \frac{hB}{k_BT} \right) \left( e^{\frac{-2hB(J+1)}{k_BT}} \right) \right] n_{total} \label{eq:7.6.21} \end{equation} $$
- The constant \(C\) includes fundamental constants $$ \begin{equation} C=\frac{2\pi}{3\varepsilon_0 ch} \label{eq:7.6.22} \end{equation} $$
/