Vibrational States
Shaun Williams, PhD
Spatial Degrees of Freedom, Normal Coordinates, and Normal Modes
- Spatial degrees of freedom are independent direction of motion
- A single atom has three spacial degrees of freedom (movement along x, y, and z)
- Motion in any other direction is a combinations of components in these directions
- Two atoms have six spatial degrees of freedom
Spatial Degrees of Freedom
- We could also say that one atom's motion can be specified as \((x_1,x_1,z_1)\)
- Two atoms, therefore, would have six spatial degrees of freedom listed as \((x_1,y_1,z_1)\) and \((x_2,y_2,z_2)\)
- In general, to locate \(N\) atoms in space, we need \(3N\) coordinates
- Therefore, a system composed of \(N\) atoms has \(3N\) spatial degrees of freedom
Example 6.1
Identify the number of spatial degrees of freedom for the following molecules: \(\chem{Cl_2}\), \(\chem{CO_2}\), \(\chem{H_2O}\), \(\chem{CH_4}\), \(\chem{C_2H_2}\), \(\chem{C_2H_4}\), \(\chem{C_6H_6}\).
Motion of Nuclei
- The motion of atomic nuclei in a molecule is not as simple as translating each of the nuclei's motion
- This is because of the chemical bonds that pull nuclei together
- In a diatomic molecule, if one atom moves, a force will be exerted on the other atom causing to to move
- This situation is like two balls coupled together by a spring
- There are, however, still 6 degrees of freedom but the motions are not quite independent
- This means that we need a new way to describe the six degrees of freedom that are independent
- We need new coordinates that are independent of each other and still account for the coupled motion
- These new coordinates are called normal coordinates and motion described by normal coordinates are called normal modes
Normal Coordinates
- A normal coordinate is a linear combination of Cartesian displacement coordinates
- A linear combination is a sum of terms with constant weighting coefficients multiplying each terms
- These coefficients can be imaginary or any positive of negative numbers.
- For example, the point or vector \(r=(1,2,3)\) in three-dimensional space can be written as a linear combination of unit vectors $$ r=1\bar{x}+2\bar{y}+3\bar{z} $$
- Cartesian displacement coordinate gives the displacement in any particular direction of an atom from it equilibrium position
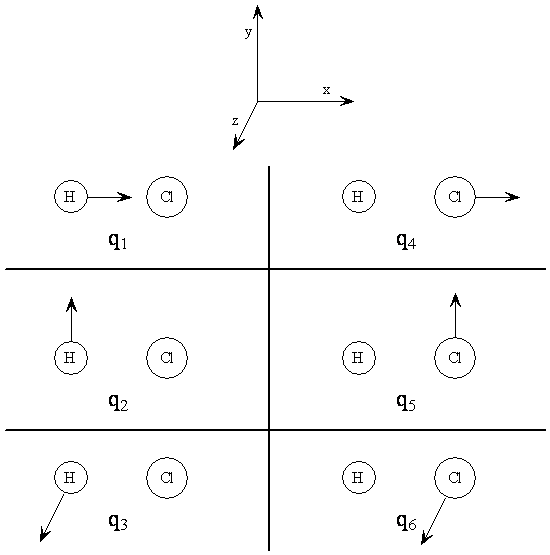
The Cartesian Displacement Coordinates for \(\chem{HCl}\)
$$ \begin{align} q_1 &= x_H - x_H^e \\ q_2 &= y_H - y_H^e \\ q_3 &= z_H - z_H^e \\ q_4 &= x_{Cl} - x_{Cl}^e \\ q_5 &= y_{Cl} - y_{Cl}^e \\ q_6 &= z_{Cl} - z_{Cl}^e \end{align} $$
Note 1: \(e\) designates the equilibrium position.
Note 2: It is customary to label displacement coordinates with the symbol \(q\)
Cartesian Displacement Coordinates for HCl
Normal Modes
- It is relatively easy to find the linear combinations that make the normal modes for a diatomic molecule from the equations two slides ago and the diagrams on the previous slide
- The combination \(q_1+q_4\) corresponds to the translation of the entire molecule in the x direction, call this normal mode \(T_x\)
- Similarly, \(T_y=q_2+q_5\) and \(T_z=q_3+q_6\) are translations in the y and z directions respectively
- We now have three normal coordinates that account for three degrees of freedom (the three translations of the entire molecule
- Now, let's try similar things: since adding worked, let's try subtracting
- Look at \(q_2-q_5\): this would have the H going in one direction and the Cl going in the opposite direction
- Because of the bond, this would result in the molecule beginning to rotate about the z-axis - we therefore call it \(R_z\)
- Similarly, \(R_y=q_3-q_6\)
Vibration
- The remaining combination, \(q_1-q_4\), corresponds to the atoms moving towards each other along the x-axis
- This motion is the beginning of a vibration
- vibrations is an oscillation of the atoms back and forth along an axis
- This vibration accounts for the sixth degree of freedom $$ Q=q_1-q_4 $$
Example 6.2
Draw and label six diagrams, each similar to the previous diagram, to show the 3 translational, 2 rotational and 1 vibrational normal coordinates of a diatomic molecule.
Distinguishing Characteristics of Normal Modes
- Normal modes should have the following distinguishing characteristics
- In a particular vibrational normal mode, the atoms move about their equilibrium positions in a sinusoidal fashion with the same frequency
- Each atom reaches its position of maximum displacement at the same time, but the direction of displacement may differ for different atoms
- Although the atoms are moving, the relationships among the relative positions of the different atoms do not change
- The center of mass of the molecule does not move
- For example, the first property says that $$ q_1 = A_1 \sin(\omega t) \text{ and } q_4 = A_4 \sin(\omega t) $$ so that $$ Q=q_1-q_4 = A_1 \sin (\omega t)-A_4 \sin (\omega t) $$
Vibration Amplitudes
- In general, the magnitude of each atom's displacement in a vibrational normal mode may be different
- In fact, some atom's displacement magnitudes in the vibration can be zero
- If the amplitude of some atom in some direction is zero, it means that the atoms does not move in that direction in that normal mode
- In different normal modes, the displacements of the atoms are different and the frequencies of the motion are generally different
- If two or more vibrational modes have the same vibrational frequency they are called degenerate
Phasing
- You may have noticed earlier that atoms in a vibration reach their extreme points in their motion at the same time
- Mathematically, the negative sign in the equation for \(Q\) accounts for this relationship
- This timing with respect to the direction of motion is called the phasing of the atoms
- In a normal mode, the atoms move with a constant phase relationship to each other
- The phase relationship is represented by a phase angle \(\phi\) in the argument of the sine function
- The angle is called the phase angle because it shifts the sine function on the time axis
- Since: \(-\sin \theta = \sin \left(\theta + 180^\circ\right)\) then $$ Q= A_1 \sin (\omega t)+A_4 \sin (\omega t + 180^\circ) $$
Center of Mass
- Recall that the center of mass for a diatomic molecule is defined as the point where $$ m_H d_H = m_{Cl}d_{Cl} $$
- The distances are the distances of these atoms from the center of mass
- In general, light atoms are located further from the center of mass than heavy atoms
- To keep the center of mass fixed during a vibration, the amplitude of motion of an atom must depend inversely on its mass - that is light atoms moves a linger distance during the vibration than do heavy atoms
More on Normal Modes
- In general, a molecule with \(3N\) spatial degrees of freedom has:
- 3 translational normal modes (along the three axes)
- 3 rotational modes (around each of the three axes)
- \(3N-6\) vibrational normal modes
- A linear molecule only has two rotational modes as we have seen
- This means that a linear molecule has \(3N-5\) vibrational normal modes
- Identifying normal modes and normal coordinates in triatomic and larger molecules is difficult. A mathematical analysis is required
Example 6.3
Identify the number of translational, rotational, and vibrational normal modes for the following molecules: \(\chem{Cl_2}\), \(\chem{CO_2}\), \(\chem{H_2O}\), \(\chem{CH_4}\), \(\chem{C_2H_2}\), \(\chem{C_2H_4}\), \(\chem{C_2H_6}\), \(\chem{C_6H_6}\).
Classical Description of the Vibration of a Diatomic Molecule
- A classical description of the vibration is needed because the first step in the quantum mechanical description begins with replacing the classical energy with the Hamiltonian operator in the Schrödinger equation
- The internal motions of vibration and rotation for a two-particle system can be described by a single reduced particle with a reduced mass \(\mu\) located at \(r\)
Vibration of a Diatomic - Coordinates

The diagram shows the coordinate system for a reduced particle. \(R_1\) and \(R_2\) are vectors to \(m_1\) and \(m_2\). \(R\) is the resultant and points to the center of mass. (b) Shows the center of mass as the origin of the coordinate system, and (c) expressed as a reduced particle.
The Vectors
- The vector \(r\) corresponds to the internuclear axis with a magnitude of the bond length
- Any change in the orientation of \(r\) corresponds to a rotation of the molecule
- Any change in length of \(r\) corresponds to a vibration of the molecule
- The change in bond length from the equilibrium bond length is the normal vibrational coordinate \(Q\) for a diatomic molecule
Using Newton's Equation of Motion
- We can begin with \( \vec{F}=m\vec{a}\)
- In this equation, the mass becomes the reduced mass \(\mu\) and the acceleration becomes \(\frac{d^2 Q}{dt^2}\)
- The force is the force that pulls the molecule back to its equilibrium bond length
- If we consider the bond behaving like a spring, then we can use Hooke's Law, \(F=-kQ\) where \(k\) is the force constant
- The potential energy in Hooke's law is $$ \begin{equation} V(Q) = \frac{1}{2}kQ^2 \label{eq:6.2.3} \end{equation} $$
- Hooke's Law or the harmonic potential is a common approximation for the vibrational oscillations of molecules
The Force Constant
- The force constant depends on the nature of the chemical bond in molecule systems
- The larger the force constant, the stiffer the spring or the stiffer the bond
- Since it is the electron distribution between the two positively charged nuclei that holds them together, a double bond with more electrons has a larger force constant than a single bond
- IR and other vibrational spectra provide information about the molecular composition of substances and about the bonding structure because of this relationship between electron density and the force constant
- It is important to note that a stiff bond with a large force constant is not necessarily a strong bond with a large dissociation energy.
Example 6.4
- Show that minus the first derivative of the harmonic potential energy function in Equation \eqref{eq:6.2.3} with respect to \(Q\) is the Hooke's Law force.
- Show that the second derivative is the force constant, \(k\).
- At what value of \(Q\) is the potential energy a minimum; at what value of \(Q\) is the force zero?
Rewriting Some Equations
- Based on the results of the previous examples, we can rewrite \(\vec{F}=m\vec{a}\) $$ \begin{equation} \frac{d^2 Q(t)}{dt^2} + \frac{k}{\mu} Q(t) = 0 \label{eq:6.2.4} \end{equation} $$
- This equation is the equation of motion for a classical harmonic oscillator
- It is a linear second-order differential equation that can be solved by the standard method of factoring and integration we saw in chapter 5
Example 6.5
Substitute the following functions into Equation \eqref{eq:6.2.4} to show that they are both possible solutions to the classical equation of motion. $$ Q(t) = Q_0 e^{i\omega t} \text{ and } Q(t)=Q_0 e^{-i\omega t} $$ where $$ \omega = \sqrt{\frac{k}{\mu}} $$ Note that the Greek symbol \(\omega\) for frequency represents the angular frequency \(2 \pi \nu\).
Example 6.6
Show that sine and cosine functions also are solutions to Equation \eqref{eq:6.2.4}.
Vibrational Energy
- The energy of the vibration is the sum of the kinetic energy and the potential energy
- The momentum associated with the vibration is $$ \begin{equation} P_Q = \mu \frac{dQ}{dt} \label{eq:6.2.7} \end{equation} $$ so the energy can be written as $$ \begin{equation} E=T+V = \frac{P_Q^2}{2\mu} + \frac{k}{2}Q^2 \label{eq:6.2.8} \end{equation} $$
Quantum Mechanical Description of the Harmonic Oscillator
Derivation of the harmonic oscillator system is quite complicated
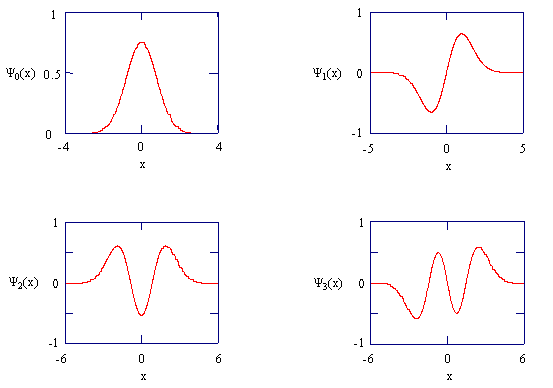
The harmonic oscillator wavefunctions describing the four lowest energy states.
Example 6.7
Consider the previous figure in terms of the magnitude of the normal coordinate \(Q\). Couch your discussion in terms of the \(\chem{HCl}\) molecule. How would you describe the location of the atoms in each of the states? How does the oscillator position correspond to the energy of a particular level?
Example 6.8
Plot the probability density for energy level 10 of the harmonic oscillator. How many nodes are present? Plot the probability density for energy level 20. Compare the plot for level 20 with that of level 10 and level 1. Compare these quantum mechanical probability distributions to those expected for a classical oscillator. What conclusion can you draw about the probability of the location of the oscillator and the length of a chemical bond in a vibrating molecule? Extend your analysis to include a very high level, like level 50.
Conclusions
- After completing these examples you should have noticed that as the quantum number increases, the probability distribution approaches that of a classical oscillator
- This observation is very general
- It was first noticed by Bohr and is called the Bohr Correspondence Principle
- The principle states that classical behavior is approached in the limit of large values for a quantum number
- A classical oscillator is most likely to be found in the region of space where its velocity is the smallest
Harmonic Oscillator Properties
Classical Harmonic Oscillator Summary
- For a classical oscillator we know exactly the position, velocity, and momentum as a function of time
- The frequency of the oscillator is determined by the effective mass \(M\) and the effective force constant \(K\) and does not change unless one of these is physically changed
- There are no restrictions on the energy of the oscillator
The Quantum Mechanical Oscillator
- In a quantum mechanical system, the oscillation frequency of a given normal mode is still controlled by the mass and the force constant
- However, the energy of the oscillator is quantized
- The allowed energy levels and equally spaces and related to the oscillator frequencies $$ \begin{equation} E_v = \left( v+\frac{1}{2} \right) \hbar \omega \label{eq:6.4.1} \end{equation} $$ with \(v=0,1,2,3,\dots\)
- In a quantum mechanical oscillator, we cannot specify the position of the oscillator or its velocity as a function of time
- We talk about the probability of the oscillator being displaced from equilibrium by a certain amount
Quantum Mechanical Oscillators and Probability
- The probability that the oscillator is displaced between a distance of \(Q\) and \(dQ\) is $$ \begin{equation} Pr\left[ Q \rightarrow Q+dQ \right] = \psi_v^*(Q) \psi_v(Q) dQ \label{eq:6.4.3} \end{equation} $$
- We can calculate the average displacement and the mean square displacement of the atoms relative to their equilibrium positions
- The average is just \(\expect{Q}\) and the mean square displacement is \(\expect{Q^2}\)
- We can also calculate average momenta \(\expect{P_Q}\) and \(\expect{P_Q^2}\)
Averages
- The potential energy function is symmetric around \(Q=0\)
- This means that we expect values of \(Q \gt 0\) to be equally as likely as \(Q\lt 0\)
- This means that the average value of \(Q\) should be zero
- This does not mean that the harmonic oscillator is stationary
- Instead, the particle is moving back and forth but has an average of zero
- Since the lowest allowed harmonic oscillator energy, \(E_0\) is \(\frac{\hbar \omega}{2}\) and not zero, the atoms in a molecule must be moving even in the lowest vibrational state
- This phenomenon is called the zero-point energy or the zero-point motion
Moving on from simple averages...
- Since the average values of displacement and momentum are all zero, we need to find other quantities that can be used to facilitate comparisons of the various normal modes
- We can use the root mean square deviations
- For a molecular vibration, these quantities represent the standard deviation in the bond length and the standard deviation in the momentum of the atoms from the average values of zero
- Effectively they provide us with a measure of the relative displacement and momentum
- Remember the Heisenberg Uncertainty Principle $$ \begin{equation} \sigma_Q \sigma_P \ge \frac{\hbar}{2} \label{eq:6.4.4} \end{equation} $$
Harmonic Oscillator Wavefunctions
- The harmonic oscillator wavefunctions form an orthonormal set which means that $$ \begin{equation} \int_{-\infty}^\infty \psi_v^*(x) \psi_v(x)dx=1 \label{eq:6.4.5} \end{equation} $$ and $$ \begin{equation} \int_{-\infty}^\infty \psi_{v'}^*(x) \psi_v(x)dx=0 \label{eq:6.4.6} \end{equation} $$ for \(v'\ne v\).
- This fact is often helpful is simplifying complicated integrals
The Classically Forbidden Region
- We can calculate the probability that a harmonic oscillator is in the classically forbidden region
- Classically, the maximum extension of an oscillator is obtained by equating the total energy of the oscillator to the potential energy
- In quantum mechanics, the wavefunctions of the quantum mechanical oscillator can extend beyond the classical limit
- The lowest allowed energy is \(E_0 =\frac{\hbar \omega}{2}\)
- Using this energy, we can find the classical limit of the amplitude of the oscillation, \(Q_0\) $$ \begin{equation} \frac{\hbar \omega}{2} = \frac{K Q_0^2}{2} \label{eq:6.4.7} \end{equation} $$
Finding the Classical Limit
- Recall that \(K\) is the effective force constant and obeys the relation $$ \begin{equation} \omega = \sqrt{\frac{K}{M}} \label{eq:6.4.8} \end{equation} $$
- Plugging that into equation \eqref{eq:6.4.7} and solving for \(Q_0\) $$ \begin{equation} Q_0^2=\frac{\hbar \omega}{K} = \frac{\hbar}{M\omega}=\frac{\hbar}{\sqrt{KM}} = \beta^2 \label{eq:6.4.9} \end{equation} $$
- We having introduced \(\beta\) to collect variable but it is also physically significant
Analysis of \(\beta\)
- \(\beta\) is the classical limit to the amplitude (maximum extension) of an oscillator at the zero-point energy
- Because of this, the variable \(x\) gives the displacement of the oscillator from its equilibrium position in unites of the maximum
- That means that \(x=1\) means the oscillator is at this classical limit and \(x=0.5\) means it is halfway there
- The classical limit for the lowest-energy state is \( Q_0 = \pm \beta\) or \( x= \frac{Q_0}{\beta}=\pm 1 \)
- Higher energy states will have higher total energies so the classical limits to their amplitudes of displacement will be larger
Example 6.9
Mark \( x = +1\) and \( x = - 1\) on the graph for \( \left| \psi_0^2 (x) \right|\) derived from the figure below and note whether the wavefunction is zero at these points.

Non-Classical
- You should have seen that the wavefunctions are not zero at the classical limit
- This means that the quantum mechanical oscillator has a finite probability of having a displacement that is larger than what is classically possible
- The oscillator can be in a region of space where the potential energy is greater than the total energy
- In some situations, a larger amplitude vibration could enhance the chemical reactivity of a molecule
- The fact the the QM oscillator can be outside the classical region is a consequence of the wave property of matter and the Heisenberg Uncertainty Principle
The Probability of Being Forbidden
- The probability of an oscillator in the forbidden region is $$ \begin{equation} Pr\left[ \text{forbidden} \right] = 1 - Pr\left[ \text{allowed} \right] \label{eq:6.4.10} \end{equation} $$
- We can evaluate this integral $$ \begin{equation} Pr\left[\text{allowed}\right] = 2 \int_0^{Q_0} \psi_0^*(Q)\psi_0(Q) dQ \label{eq:6.4.11} \end{equation} $$
- Remember that for \(v=0\), \(Q=Q_0\) corresponds to \(x=1\)
- Doing some math behind the scenes $$ \begin{equation} Pr\left[ \text{allowed}\right] = \frac{2}{\sqrt{\pi}} \int_0^1 e^{-x^2} dx \label{eq:6.4.12} \end{equation} $$
Analysis of the Probability
- The integral in equation \eqref{eq:6.4.12} is called an error function (ERF), and can only be evaluated numerically
- Value can be found in books of mathematical tables or using mathematical software
- When the limit of integration is 1, \( ERF(1)=0.843 \) and therefore \(Pr\left[ \text{forbidden}\right]=1-0.843=0.157\)
- This results means that the quantum mechanical oscillator can be found in the forbidden region 15.7% of the time.
- This effect leads to the phenomenon of quantum mechanical tunneling
Quantum Mechanical Tunneling
- Quantum mechanical tunneling is a consequence of the fact that a vibrating molecule has a significant probability to be in the classically forbidden region of space
- Suppose we have a double potential well with a finite potential energy barrier between them
- Let's think about what will happen in this case
Double-Well Potential
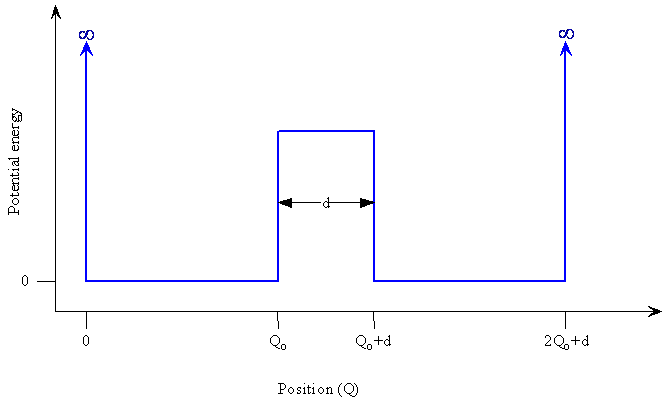
A double-well potential. The potential energy of an atom as a function of its position in space.
The Double-Well Wavefunction
- How might the wavefunction in this double-well potential look?
- A reasonable start would be to consider a harmonic oscillator in each well
- Because of the asymptotic approach to zero, the functions extend into the region of the barrier
- These functions can connect up to each other if the barrier is not too high or wide
- The connection of the two functions means that a particle starting out in the left well has a probability of tunneling through the barrier to the right side
- Tunneling has been proposed to explain electron transfer in some enzyme reactions and to account for mutations of DNA base pairs as a hydrogen atom in a hydrogen bond tunnels through the barrier from one base to the other
Harmonic Oscillator Selection Rules
- Photons can be absorbed or emitted and the harmonic oscillator can go from one vibrational state to another
- Which transitions between vibrational states are allowed?
- If we take an infrared spectrum of a molecule, we see numerous absorption and we need to relate those bands to allowed transitions
Transition Moment
- The selection rules are determined by the transition moment integral $$ \begin{equation} \mu_T = \int_{-\infty}^\infty \psi_{v'}^*(Q) \hat{\mu} \psi_v(Q) dQ \label{eq:6.6.1} \end{equation} $$
- To evaluate this integral we need to express the dipole moment operator, \( \hat{\mu} \), in terms of the magnitude of the normal coordinate \(Q\)
- The dipole moment operator is defined as $$ \begin{equation} \hat{\mu} = \sum_{\text{electrons}} er + \sum_{\text{nuclei}} qR \label{eq:6.6.2} \end{equation} $$ with particle charges (\(-e\) and \(q\)) and position vectors (\(r\) and \(R\))
- We can put the dipole moment operator in terms of the magnitude of the normal coordinate, \(Q\), by using a Taylor series expansion
Rewriting the Dipole Moment Operator
- The Taylor series expansion for the dipole moment is $$ \begin{equation} \mu(Q) = \mu_{Q=0} + \left( \frac{d\mu(Q)}{dQ}\right)_{Q=0} Q + \left( \frac{d^2 \mu(Q)}{dQ^2} \right)_{Q=0} Q^2 + \dots \label{eq:6.6.3} \end{equation} $$
- Retaining only the first two terms and substituting it into equation \eqref{eq:6.6.1} gives us $$ \begin{equation} \mu_T = \begin{split} & \mu_{Q=0} \int\limits_{-\infty}^\infty \psi_{v'}^* (Q) \psi_v(Q) dQ \\ & \;\;\;\; + \left( \frac{d\mu(Q)}{dQ} \right)_{Q=0} \int\limits_{-\infty}^\infty Q\psi_{v'}^*(Q) \psi_v(Q)dQ \end{split} \label{eq:6.6.4} \end{equation} $$
Analysis of Equation \eqref{eq:6.6.4}
- \(\mu_{Q=0}\) is the dipole moment when the nuclei are at their equilibrium position
- \(\left( \frac{d\mu(Q)}{dQ} \right)_{Q=0} \) is the linear change in the dipole moment due to the displacement of the nuclei in the normal mode
- Both \(\mu\) and \(\left( \frac{d\mu(Q)}{dQ} \right)_{Q=0} \) are moved outside of the integral because they are constants that no longer depend on \(Q\) because they are evaluated at \(Q=0\)
- The integral in the first term in equation \eqref{eq:6.6.4} is 0 because any two harmonic oscillator wavefunction are orthogonal
- The integral in the second term in the equation is zero except when \(v'=v\pm 1\) (I'm not going to prove this)
- Also, the second term is zero if \(\left( \frac{d\mu(Q)}{dQ} \right)_{Q=0} =0 \) - that is, if the dipole moment does not change through the normal mode motion
Relating Back to Spectra
- This all means that if we observe absorption of IR radiation due to vibrational transition in a molecule, the transition moment cannot be zero
- We also know that the dipole moment derivative cannot be zero
- We also know that the vibrational quantum number changes by one unit
- So $$ \begin{equation} \text{For allowed transitions }\Delta v=\pm 1 \label{eq:6.6.6} \end{equation} $$
- For oxygen and nitrogen molecules, because they are symmetrical their dipole moments are zero so \(\mu_T=0\)
- Since any vibration would preserve this symmetry, \(\left( \frac{d\mu(Q)}{dQ} \right)_{Q=0} =0 \)
- So, these molecules can't absorb IR radiation in vibrational motion
/