Lecture 9
The Gaseous State
Shaun Williams, PhD
The Behavior of Gases
Properties of Gas Molecules
- Gases consist of particles that are relatively far apart (as compared to liquids and solids).
- This results in observed properties:
- Lower densities
- Compressible by applying external pressure
- This results in observed properties:
- Gas particles move about rapidly.
- Gas particles have little effect on one another unless they collide.
- When they collide, gas particles simply bounce off one another.
- Gases expand to fill containers.
- Take volume and shape of their containers
Effect of Temperature and Density
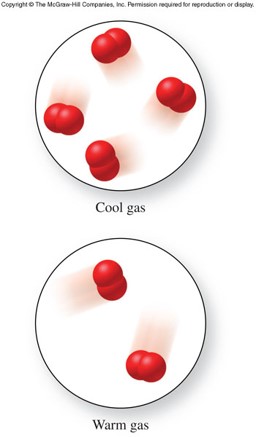
- All gases expand if heated and contract if cooled.
- Heat increases the kinetic energy of gas particles, making them move faster and farther apart.
- Since the gas particles move farther apart, there are fewer particles within a given volume.
- Therefore, warm gases have lower densities.
Physical Effect of Temperature and Density

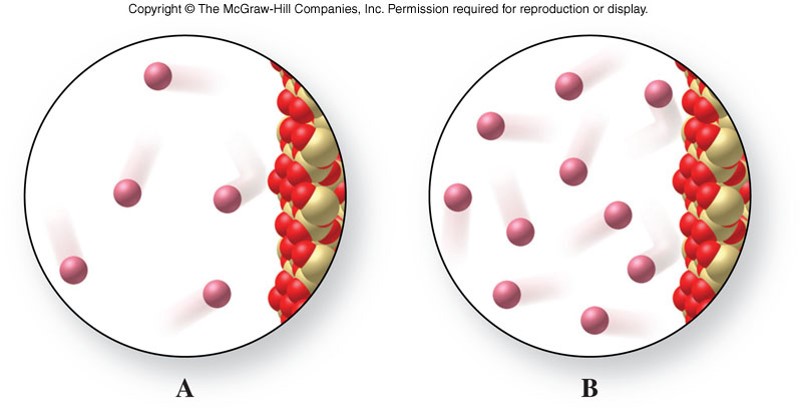
Pressure
- Is amount of force applied per unit area \[ P=\frac{\chem{force}}{\chem{area}} \]
- For a gas in a container: \[ P=\frac{\text{force of gas particles}}{\text{area of container}} \]

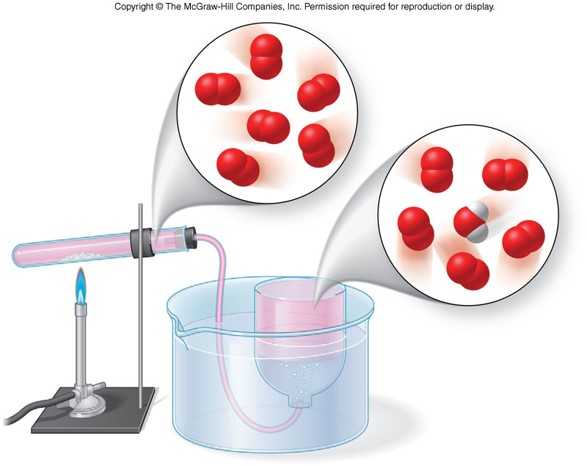
Crushing a Can

Pressure
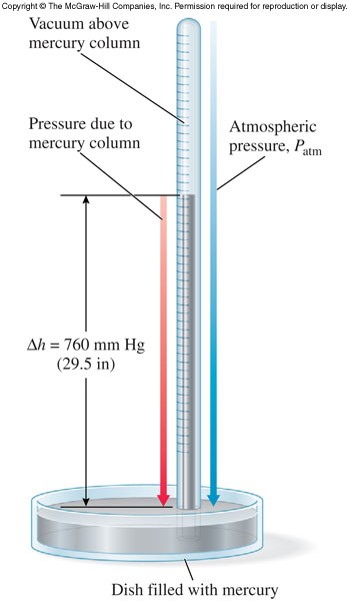
- Pressure is measured using a barometer.
- Units of pressure
- \( 1\, atm = 760\, mm\, Hg \) (mm Hg and torr are the same)
- \( 1\, atm = 14.7\,\bfrac{lb}{in^2} \) (psi)
- \( 1\, atm = 101325\, Pa \)
Factors That Affect the Properties of Gases
- Volume
- Measured in liters (L)
- Pressure
- Measured in atmospheres (atm)
- Temperature
- Measured in Kelvin (K)
- Amount of particles
- Measured in moles
- An ideal gas is a gas that behaves according to predicted linear relationships

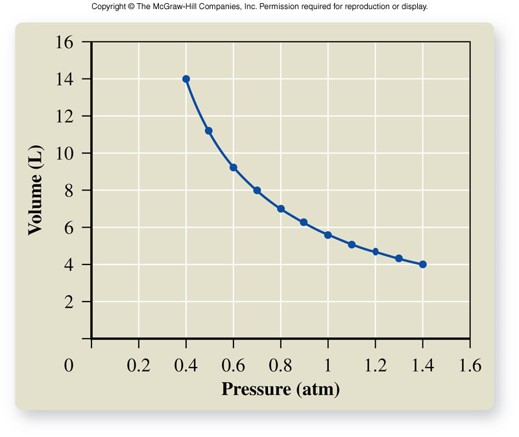
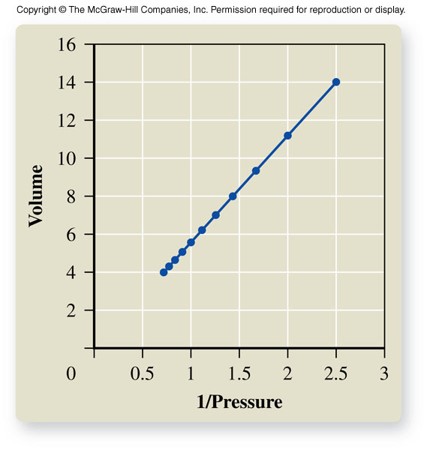
Volume vs. Pressure
Boyle's Law
- For a given mass of gas at constant temperature, volume varies inversely with pressure. \[ V \propto \frac{1}{P} \] \[ P_1V_1 = P_2V_2 \]
- As volume increases, pressure decreases.
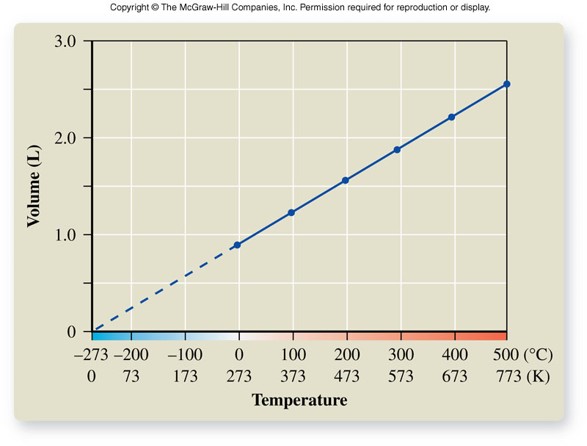
Volume vs. Temperature

Charles' Law
- For a given mass of gas at constant pressure, volume is directly proportional to temperature on an absolute (kelvin) scale. \[ T_K=T_{{}^\circ C} + 273.15 \] \[ V \propto T_K \] \[ \frac{V_1}{T_1} = \frac{V_2}{T_2} \]
- As volume increases, temperature increases.
Combined Gas Law
- For a constant amount of gas, volume is proportional to absolute temperature divided by pressure. \[ V \propto \frac{T}{P} \] \[ \frac{P_1V_1}{T_1} = \frac{P_2V_2}{T_2} \]
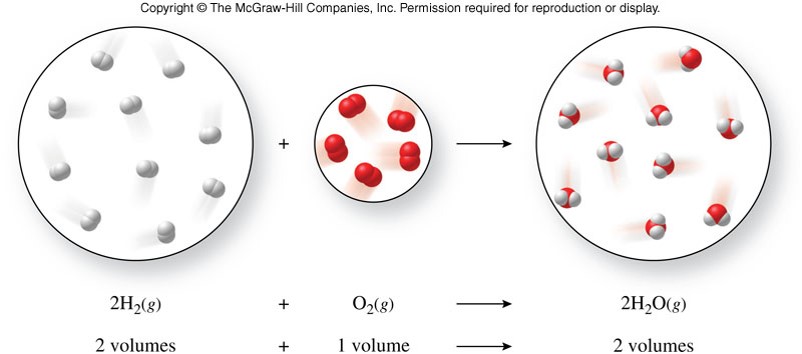
Combining Volumes
- Gay-Lussac's law of combining volumes
- Gases combine in simple whole-number volume proportions at constant temperature and pressure.
Avogadro's Hypothesis
- The volume occupied by a gas at a given temperature and pressure is directly proportional to the number of gas particles and thus to the moles of gas. \[ V \propto n \] \[ \frac{V_1}{n_1} = \frac{V_2}{n_2} \]
- As volume increases, the moles of gas increase.
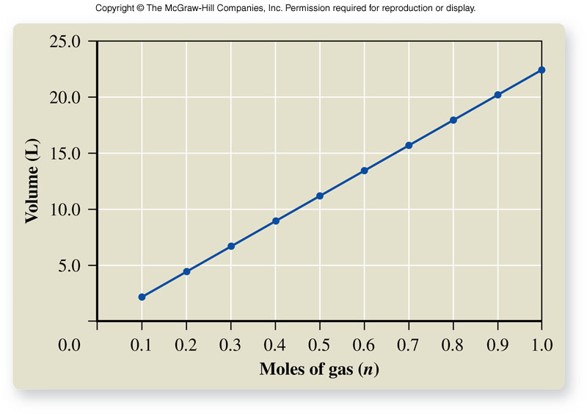
Avogadro's Hypothesis (cont.)
- At a given pressure and temperature, equal volumes of all gases contain equal numbers of moles (or particles).
- This hypothesis was measured at standard temperature and pressure (STP): \( 0^\circ C \) and \( 1\, atm \)
- The volume of an ideal gas at STP is called its molar volume: 1 mole of gas = 22.414 L
Summary of The Gas Laws
- Boyle's law \[ V \propto \frac{1}{P} \text{ at constant T, n} \]
- Charles's law \[ V \propto T \text{ at constant P, n} \]
- Avogadro's hypothesis \[ V \propto n \text{ at constant T, P} \]
- Combining them all into one proportionality: \[ V \propto \frac{nT}{P} \]
The Ideal Gas Law
- We can express the previous statement as an equality: \[ V = \text{constant}\times \frac{nT}{P} \]
- This constant is called the ideal gas constant, \(R\).
- This gives us the Ideal Gas Law: \[ V=R\times \frac{nT}{P} \xrightarrow{\text{algebra}} PV=nRT \]
- \(R\) is calculated at STP using the molar volume of a gas: \[ R=0.08206\,\frac{\chem{L\cdot atm}}{\chem{K\cdot mol}} \]
Density of a Gas
\[ \text{Density}=\frac{\text{mass}}{\text{volume}} \]
- We can solve for density in the Ideal Gas Law using substitution: \[ PV=nRT \] \[ n=\bfrac{m}{MM} \] \[ PV=\frac{mRT}{MM} \] \[ \frac{P\left(MM\right)}{RT} =\frac{m}{V} = d \]
Dalton's Law of Partial Pressures
- Gases in a mixture behave independently and exert the same pressure they would exert if they were in a container alone. \[ P_\text{total} = P_A+P_B+P_C+\cdots \] \[ P_\text{total} = P_\text{dry air} + P_\text{water} \]
Vapor Pressure of Water at Various Temperatures
| Temperature (\({}^\circ C\)) | Vapor Pressure (torr) | Temperature (\({}^\circ C\)) | Vapor Pressure (torr) |
|---|---|---|---|
| 0 | 4.6 | 28 | 28.3 |
| 5 | 6.5 | 29 | 30.0 |
| 10 | 9.2 | 30 | 31.8 |
| 15 | 12.8 | 35 | 42.2 |
| 16 | 13.6 | 40 | 55.3 |
| 17 | 14.5 | 45 | 71.9 |
| 18 | 15.5 | 50 | 92.5 |
| 19 | 16.5 | 60 | 149.4 |
| 20 | 17.5 | 70 | 233.7 |
| 21 | 18.6 | 80 | 355.1 |
| 22 | 19.8 | 90 | 525.8 |
| 23 | 21.1 | 100 | 760.0 |
| 24 | 22.4 | 110 | 1074.6 |
| 25 | 23.8 | 150 | 3570.5 |
| 26 | 25.2 | 200 | 11659.2 |
| 27 | 26.7 | 300 | 64432.8 |
Kinetic-Molecular Theory of Gases
- A model that explains experimental observations about gases under normal temperature and pressure conditions that we encounter in our environment
- Has 5 postulates:
- Gases are composed of small and widely separated particles (molecules or atoms).
- Low volumes of particles
- Low densities of gas
- High compressibility
- Gases are composed of small and widely separated particles (molecules or atoms).
Kinetic-Molecular Theory of Gases (cont.)
- Postulates continued:
- Particles of a gas behave independently of one another.
- Independent movement, unless two particles collide.
- No forces of attraction or repulsion operate between and among gas particles.
- Each particle in a gas is in rapid, straight-line motion, until it collides with another molecule or with its container.
- When collisions occur, the collisions are perfectly elastic.
- Energy transferred from one particle to another with no net loss of energy.
- Particles of a gas behave independently of one another.
Kinetic-Molecular Theory of Gases (cont. again)
- Postulates continued:
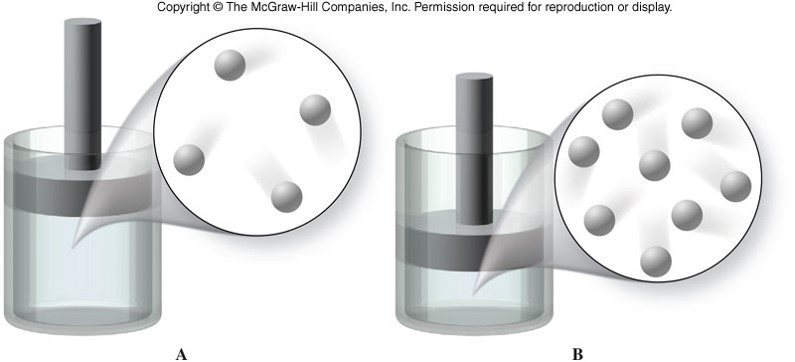
- The pressure of a gas arises from the sum of the collisions of the particles with the walls of the container.
- The smaller the container, the more collisions between the gas particles and the walls of the container, resulting in higher pressures.
- Predicts pressure should be proportional to the number of gas particles.
- The pressure of a gas arises from the sum of the collisions of the particles with the walls of the container.
Kinetic-Molecular Theory of Gases (concluded)
- Postulates continued:
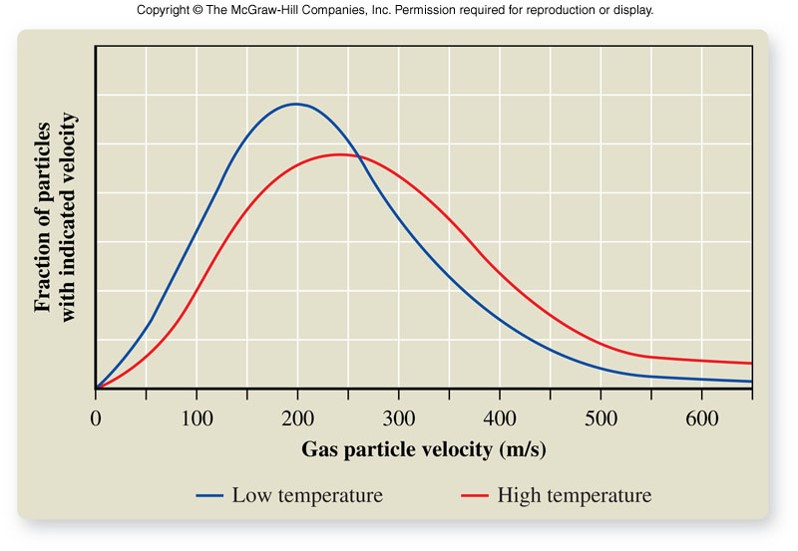
- The average kinetic energy of gas particles depends on the absolute temperature.
- Relationship between kinetic energy (\(KE\)) and velocity (\(v\)) of the gas particles: \[ KE_{av} = \frac{1}{2} mv_{av}^2 \]
- The average velocity for gas particles is greater at higher temperatures.
- Thus, if the particles move faster, they hit the walls of the container more often, resulting in higher pressure.
- The average kinetic energy of gas particles depends on the absolute temperature.
The 5th Postulate
Effect of the Kinetic-Molecular Theory of Gases
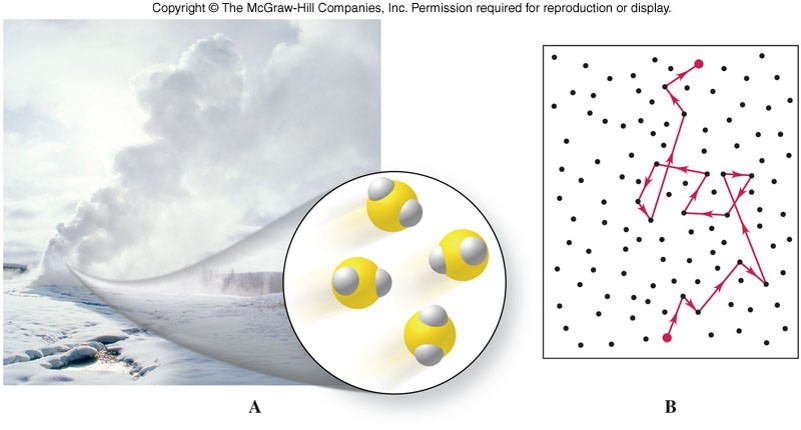
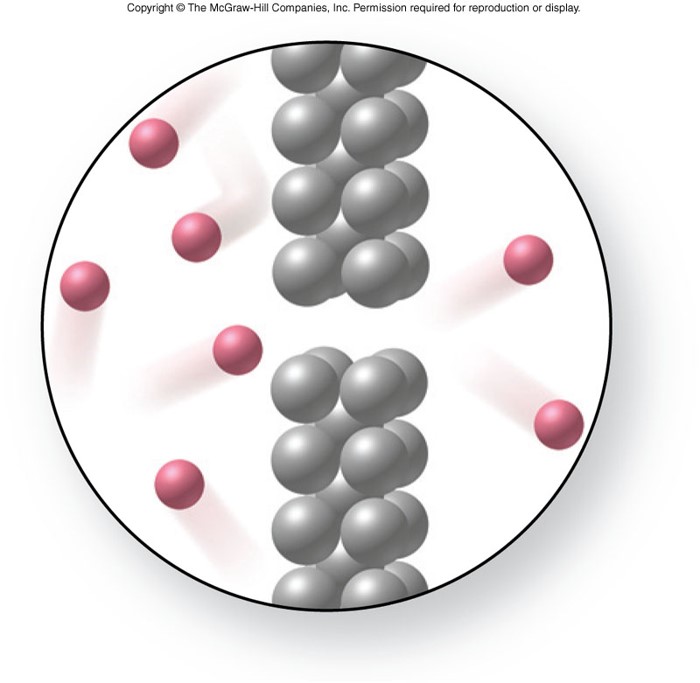
Diffusion
- The movement of gas particles from regions of high concentration to regions of low concentration. \[ KE_{av} = \frac{1}{2}mv_{av}^2 \]
- Gases have different average velocities even though they all have the same average kinetic energy.
- Light molecules or atoms move faster than heavy molecules or atoms.

Effusion
- The passage of a gas through a small opening.
- Smaller particles effuse faster than larger ones.
Gases and Chemical Reactions
- We can convert from volume to moles or moles to volume using the Ideal Gas Law as our conversion factor. \[ \text{Vol A} \xrightarrow{PV=nRT} \text{Mol A} \xrightarrow{\text{Mole ratio}} \text{Mol B} \xrightarrow{PV=nRT} \text{Vol B} \]
- We can put mass into our conversion \[ \text{Mass A} \xrightarrow{\text{Molar Mass}} \text{Mol A} \xrightarrow{\text{Mole ratio}} \text{Mol B} \xrightarrow{\text{Molar Mass}} \text{Mass B} \] \[ \text{Vol A} \xrightarrow{PV=nRT} \text{Mol A} \xrightarrow{\text{Mole ratio}} \text{Mol B} \xrightarrow{\text{Molar Mass}} \text{Mass B} \]
/