Lecture 7

Electron Structure of the Atom

Shaun Williams, PhD

Electromagnetic Radiation and Energy

White Light

• Is composed of different colors that can be separated by a prism
  • Water acts as a prism for sunlight, giving the effect of a rainbow
• Sources of white light
  • Sun
  • Regular (incandescent) light bulbs

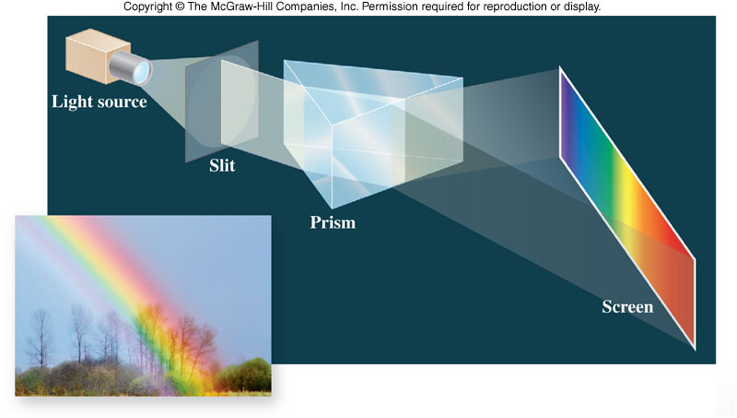
Electromagnetic Radiation

• A form of energy
• Travels through space at the speed of light (\(3.0 \times 10^8 \bfrac{m}{s}\)) as oscillating waves
• Is both an electric and a magnetic field
• Also called radiant energy
• Some examples of EM radiation
  • Light
  • X-rays

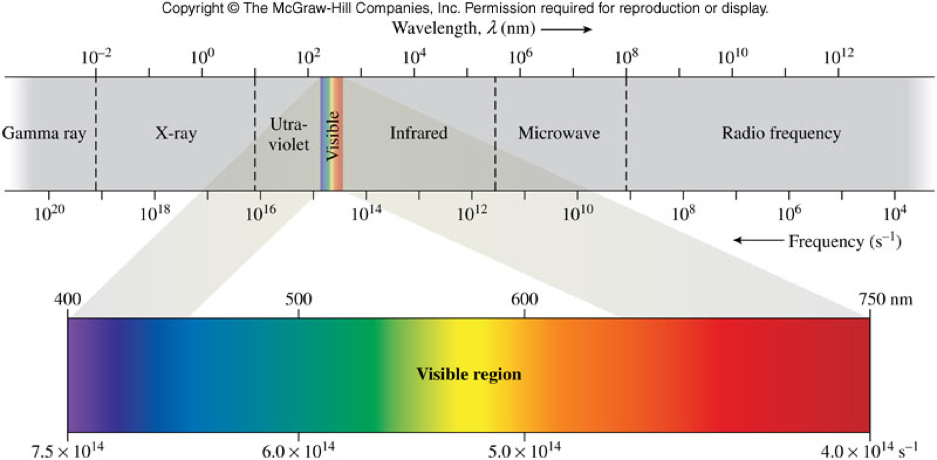
Differentiating the Kinds of Electromagnetic Radiation - Wavelength

• Wavelength (\( \lambda \))
  • The distance between two corresponding points on a wave
  • Units are same as length - m, or commonly nm (\( 10^{-9}\, \chem{m}\))

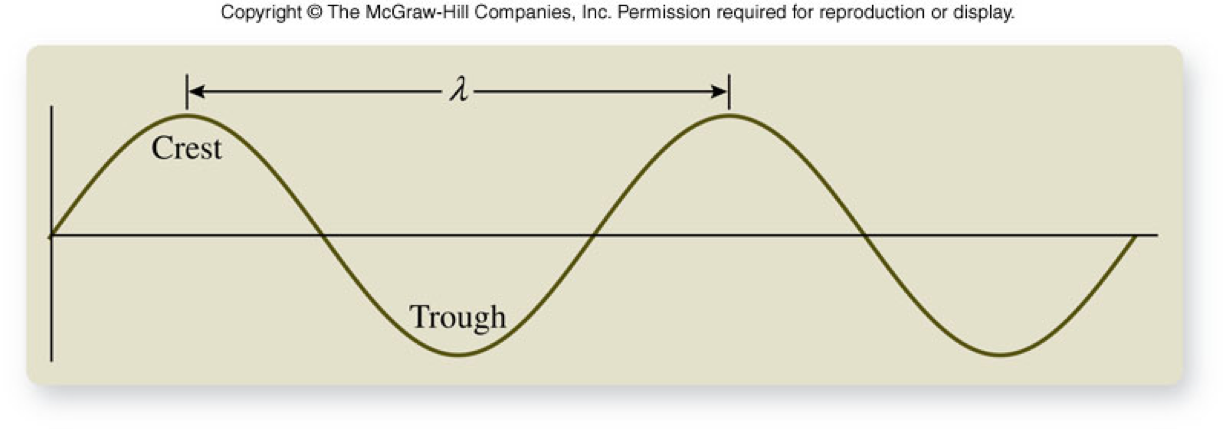
Differentiating the Kinds of Electromagnetic Radiation - Frequency

• Frequency (\(\nu\))
  • A measure of the number of wave cycles that move through a point in space in 1 s
  • Units are hertz (Hz) which are the same as inverse seconds (1/s)

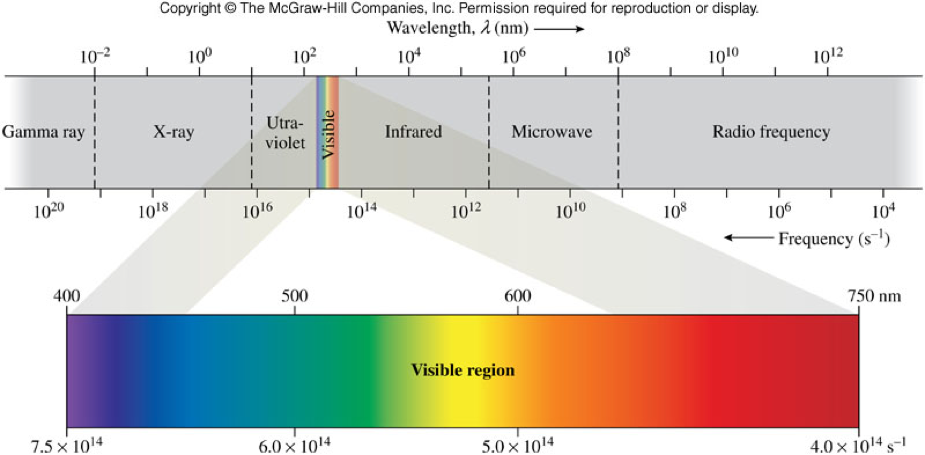
Frequency, Wavelength, and the Electromagnetic Spectrum

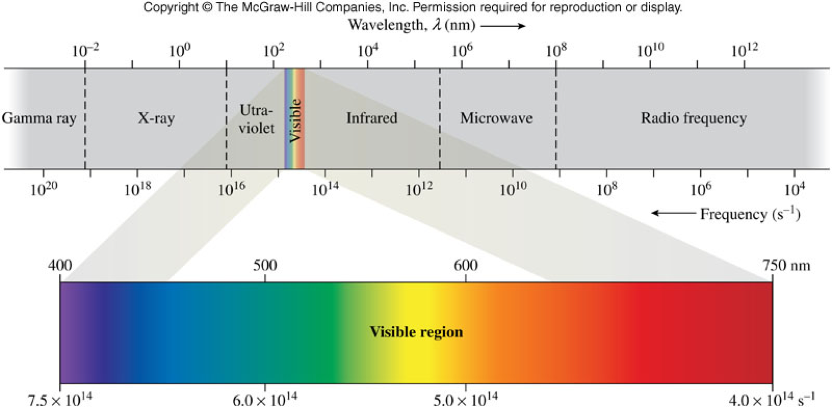
• Frequency and wavelength are inversely proportional
  • i.e. as one increases the other decreases \[ c=\lambda \nu \] Where \(c\) = speed of light (\(3.0 \times 10^8 \bfrac{m}{s}\)), \(\lambda\) = wavelength (in meters), and \(\nu\) = frequency (in Hz)

Duality of Light

• Light exists as both waves and particles (or packets of light called photons)
  • Characteristics of waves
    • Frequency
    • Wavelength
    • \(c=\lambda \nu\)
  • Characteristic of photons
    • Energy of a photon
      • Is directly proportional to the frequency and inversely proportional to the wavelength \[ E_{photon}=h\nu \] Where \(E_{photon}\) = energy of the photon (in Joules), \(h\) = Planck's constant (\(6.626 \times 10^{-34} Js\)), and \(ν\) = frequency (in Hz)

\(\lambda\), \(\nu\), and \(\chem{E_{photon}}\)

\[ c=\lambda \nu \;\;\;\;\;\;\; \chem{E_{photon}}=h\nu \]

• Using algebra, we can manipulate these two equations several ways:
• For \(c = \lambda \nu\),
  • We can solve for \(\lambda\): \(\lambda = \bfrac{c}{\nu}\)
  • or \(\nu\): \(\nu=\bfrac{c}{\lambda}\)
• For \(\chem{E_{photon}} = h\nu\)
  • We can substitute \(\bfrac{c}{\lambda}\) for \(\nu\), giving us the equation: \[ \chem{E_{photon}} = \frac{hc}{\lambda} \]
• This equation shows the inverse proportionality between \(\chem{E_{photon}}\) and \(\lambda\) (wavelength)

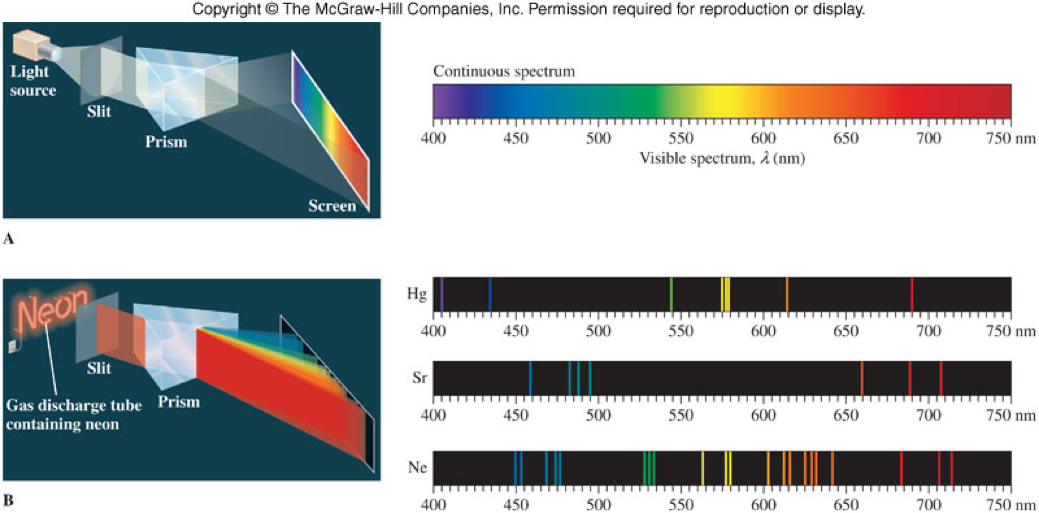
Energy is Quantized!

• Max Planck first hypothesized that energy produced by atoms can only have certain values and is therefore quantized.
• That's the reason why only distinct lines are seen in element line spectras. Energy is quantized and can only exist at certain wavelengths.

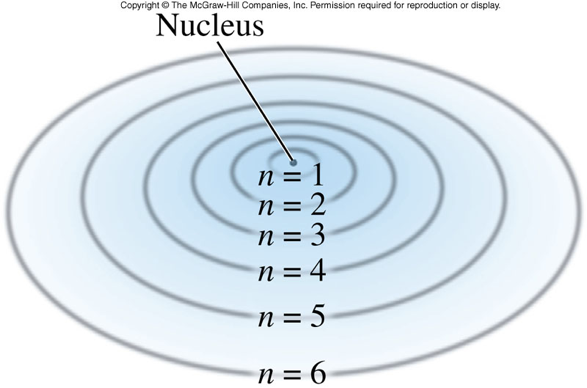
The Bohr Model of the Hydrogen Atom

• Niels Bohr hypothesized that electrons orbit the nucleus just as the planets orbit the sun (planetary model) and have fixed radii.
• He labeled the electron orbits with a number, starting with 1 closest to the nucleus and increasing as the orbits get further away from the nucleus.
  • This number is known as the Principal Quantum Number (\(n\)).

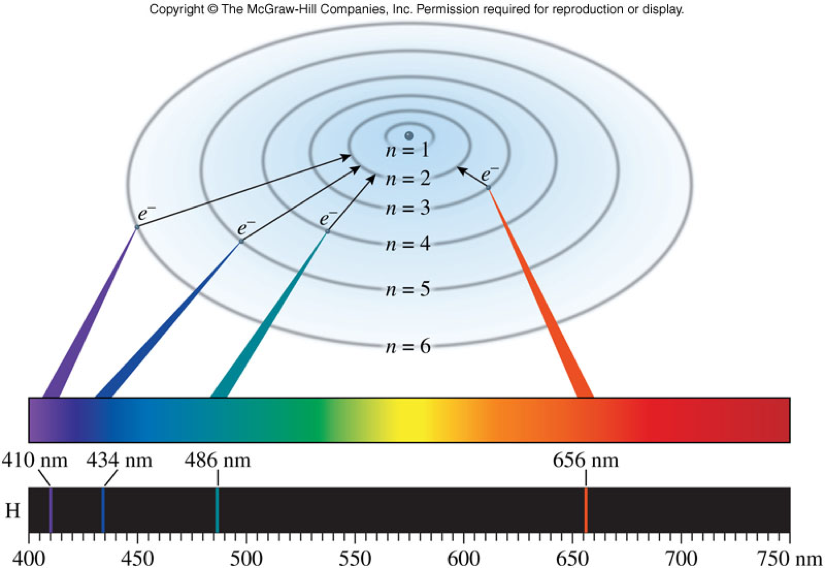
Bohr Model and Light

• The orbit with the lowest energy is closest to the nucleus. The energy of each orbit increases as the orbits get further away from the nucleus.
• When an electron jumps from one orbit to another, it absorbs or emits energy according to the equation: \(\Delta E = E_f – E_i\)

The Modern Model of the Atom

• The modern model of the atom is based on Schrödinger's mathematical model of waves
• This model describes electrons as occupying orbitals, not orbits.
  • Orbitals
    • Three dimensional regions in space where electrons are likely to be found, not a circular pathway
  • Principal energy level
    • Orbitals of similar size

Energy Levels

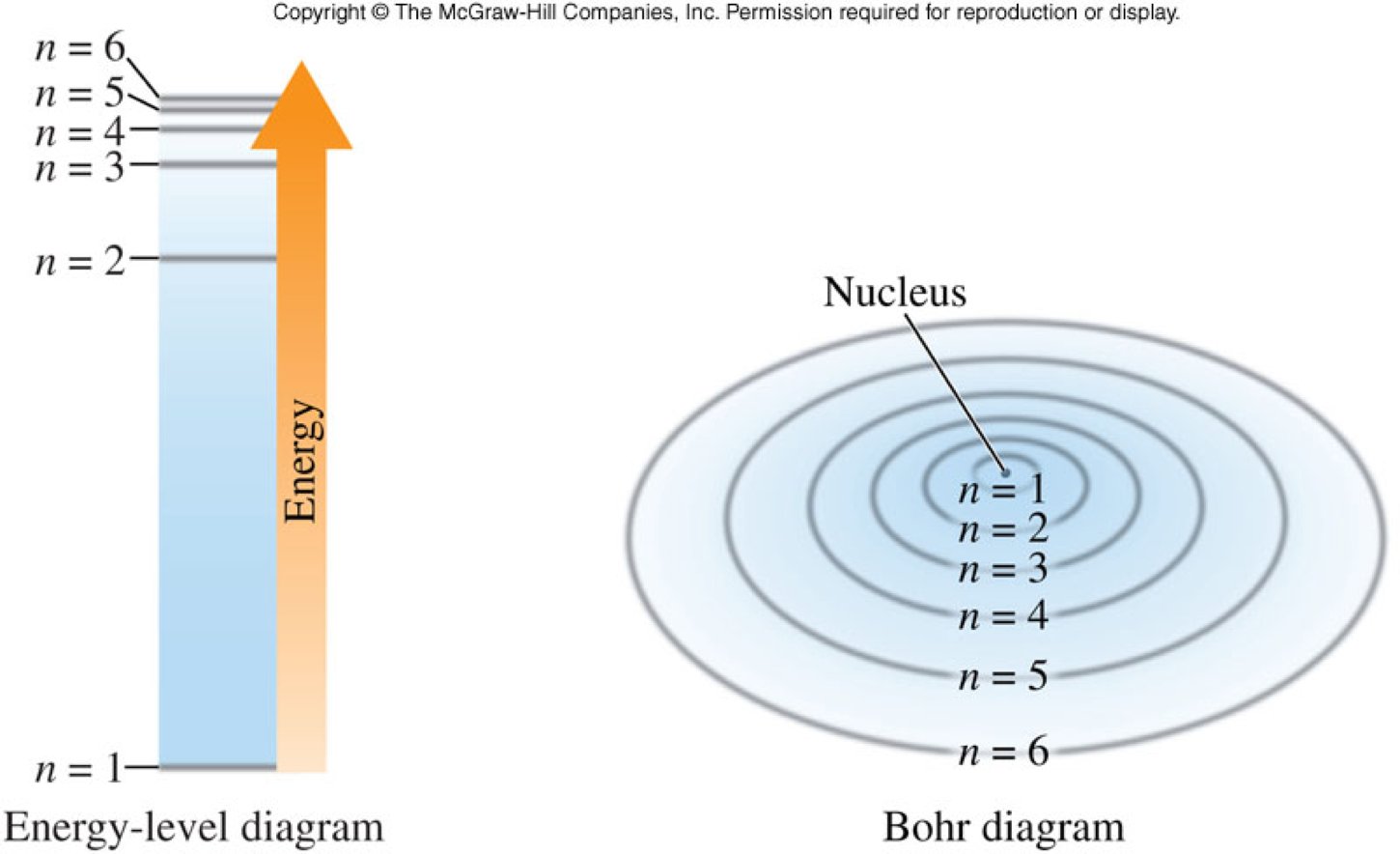
Orbitals

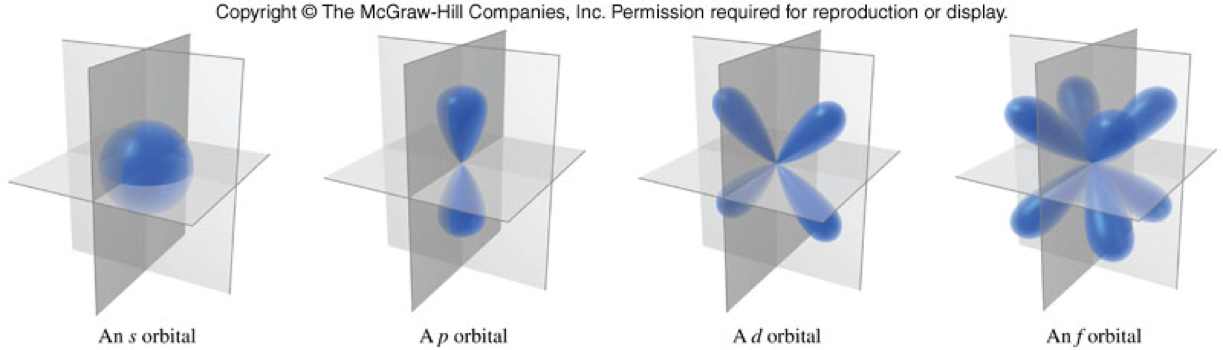
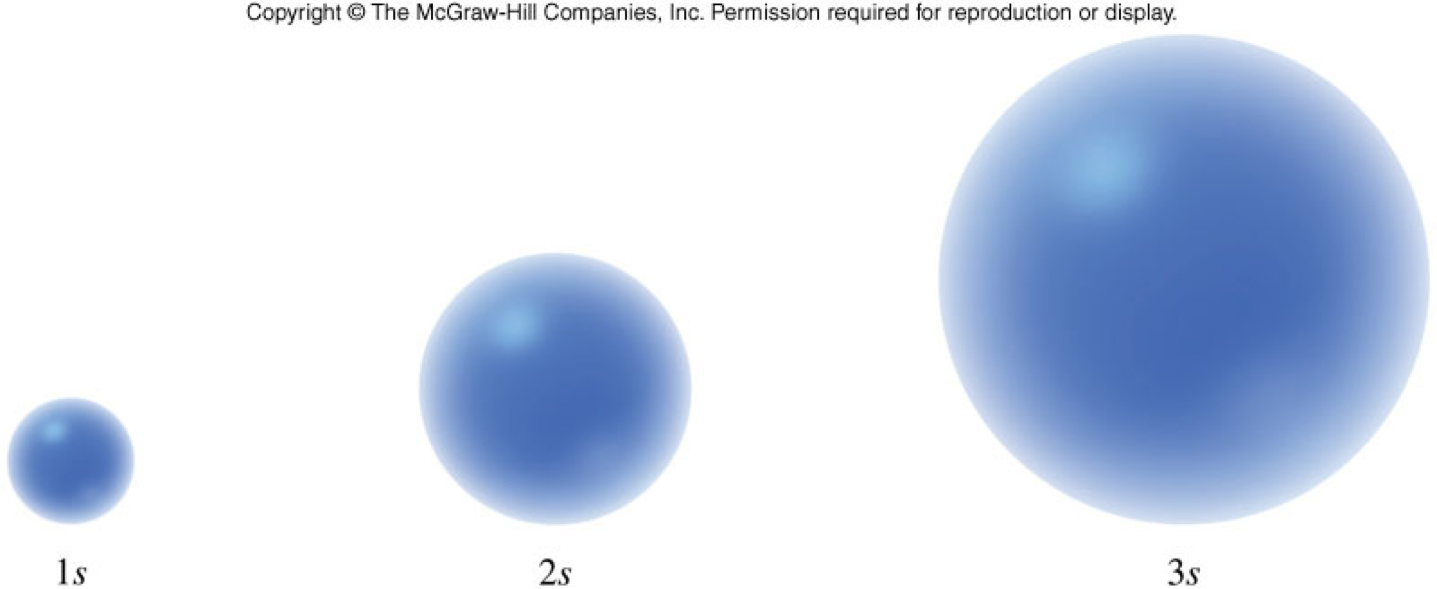
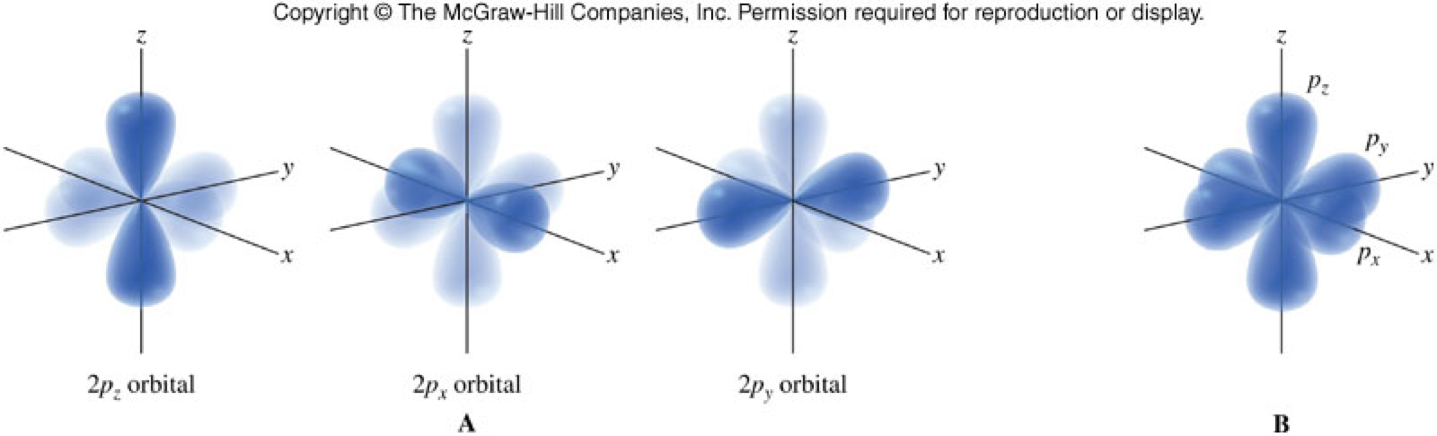
• Come in different shapes and sizes.
  • Lower energy orbitals are smaller.
  • Higher energy orbitals are larger and extend further away from the nucleus.
• Four most common types are \(s\), \(p\), \(d\), and \(f\).
• Also known as sublevels
  • Consists of just one type of orbital at a specific energy level
  • The number of sublevels is equal to \(n\), the Principal Quantum Number

\(s\)-Orbitals

\(p\)-Orbitals

\(d\)-Orbitals

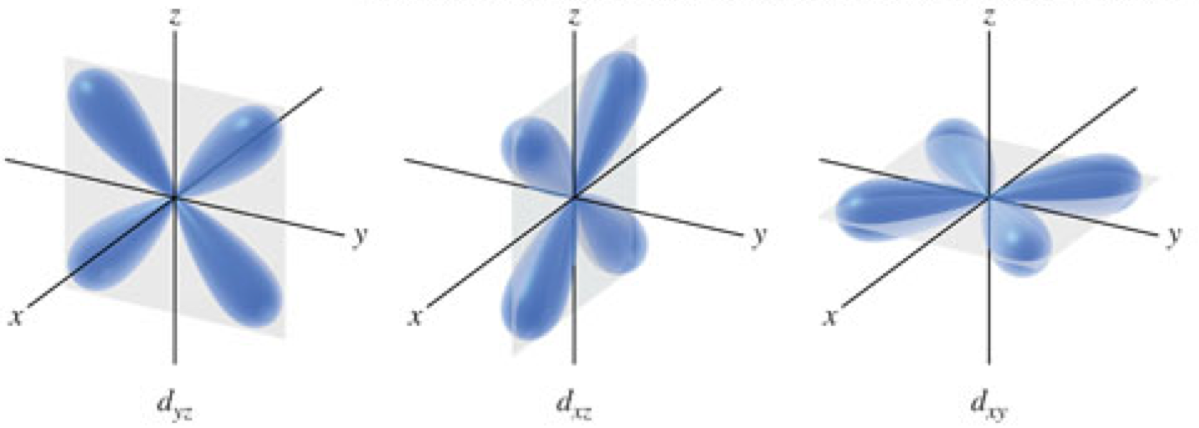
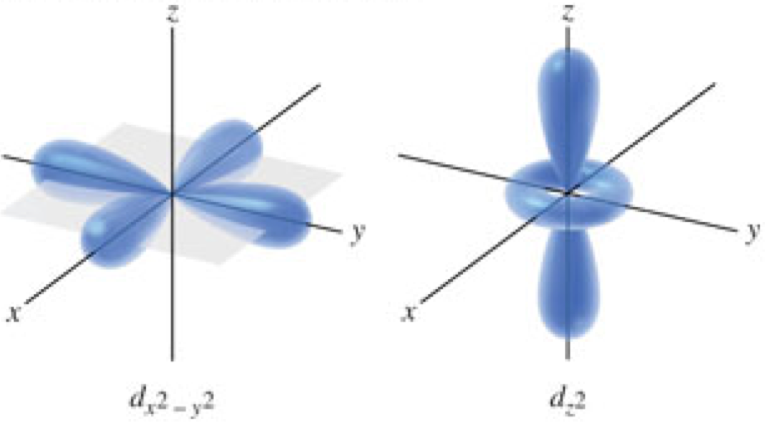
Orbital Diagrams

• Orbital diagrams
  • Show the sublevels and orbitals that can exist at each principal energy level
  • Each box represents an orbital
  • Groups of boxes represent sublevels

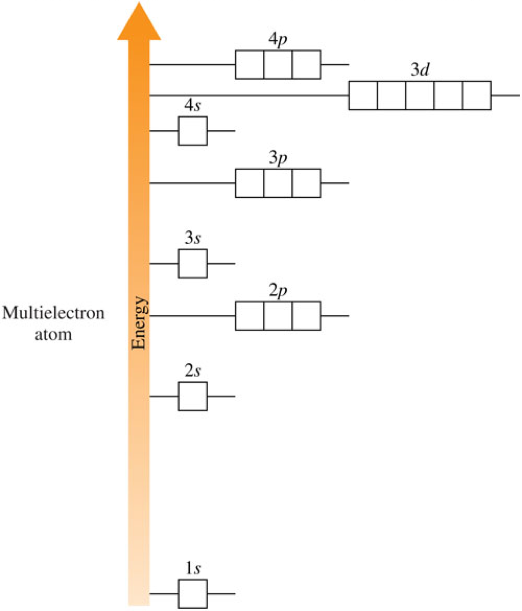
Orbital Diagrams Rules

• Two principles and 1 rule determine how the electrons are filled in the principal energy levels and sublevels.
  • Aufbau principle
    • Electrons fill orbitals starting with the lowest-energy orbitals.
  • Pauli exclusion principle
    • A maximum of two electrons can occupy each orbital, and they must have opposite spins.
  • Hund's rule
    • Electrons are distributed into orbitals of identical energy (same sublevel) in such a way as to give the maximum number of unpaired electrons.

Filling Orbitals Diagrams

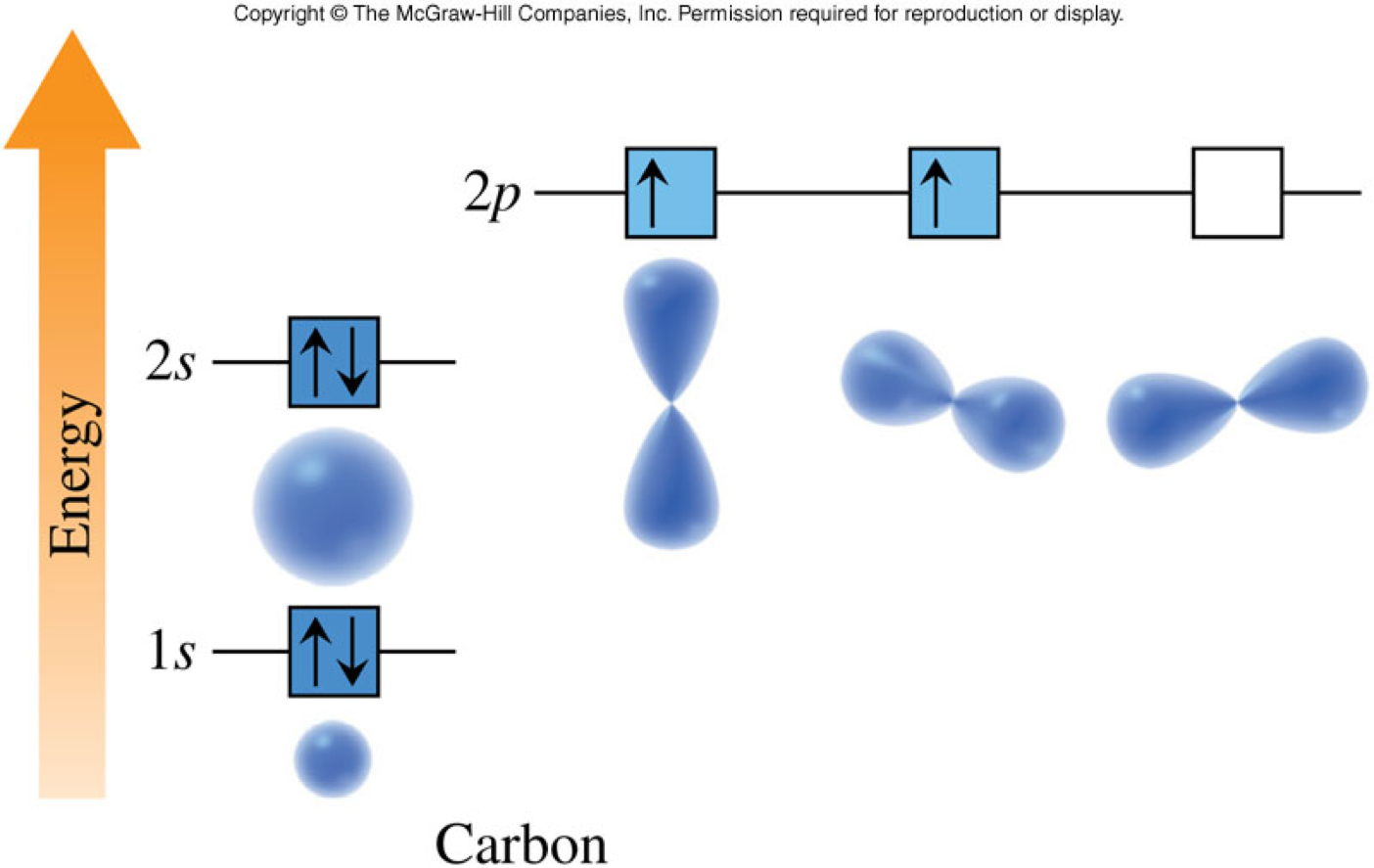
Orbital Diagrams for the 1^st Ten Elements

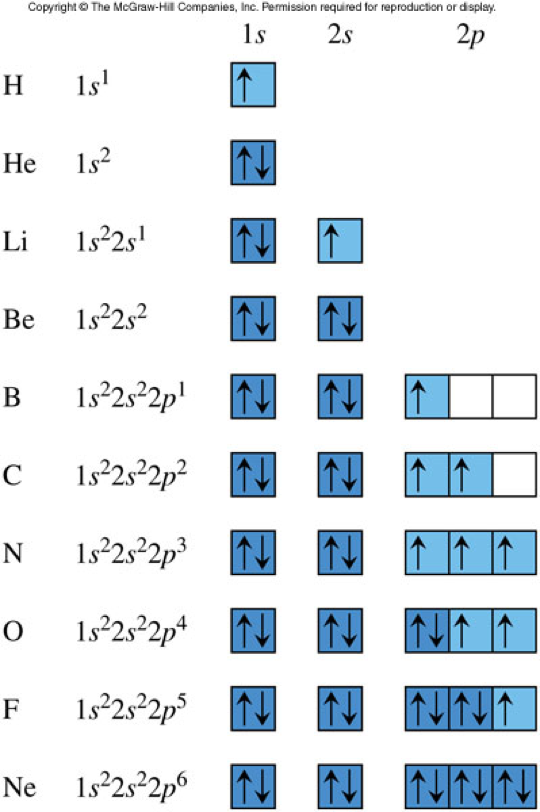
Orbital Diagrams Rules

• Shorthand notation which shows the distribution of electrons among sublevels
• When we write electron configurations, we write the number of the principal quantum number followed by a symbol for the sublevel, and then add a superscript to each sublevel symbol to designate the number of electrons in that sublevel.
• Carbon has 6 electrons. Therefore, using the orbital diagram we obtain: \[ \chem{1s^22s^22p^2} \]

Periodicity of Electron Configurations

• Can you tell the patterns among the following groups of elements?
  • Alkali Metals (Group IA (1))

    Li	\(\chem{1s^22s^1}\)
    Na	\(\chem{1s^22s^22p^63s^1}\)

  • Alkali Earth Metals (Group IIA (2))

    Mg	\(\chem{1s^22s^22p^63s^2}\)
    Ca	\(\chem{1s^22s^22p^63s^23p^64s^2}\)

  • Halogens (Group VIIA (17))

    Cl	\(\chem{1s^22s^22p^63s^23p^5}\)
    Br	\(\chem{1s^22s^22p^63s^23p^64s^23d^{10}4p^5}\)

  • Noble Gases (Group VIIIA (18))

    Ne	\(\chem{1s^22s^22p^6}\)
    Ar	\(\chem{1s^22s^22p^63s^23p^6}\)

The Principal Quantum Number and Sublevel on the Periodic Table

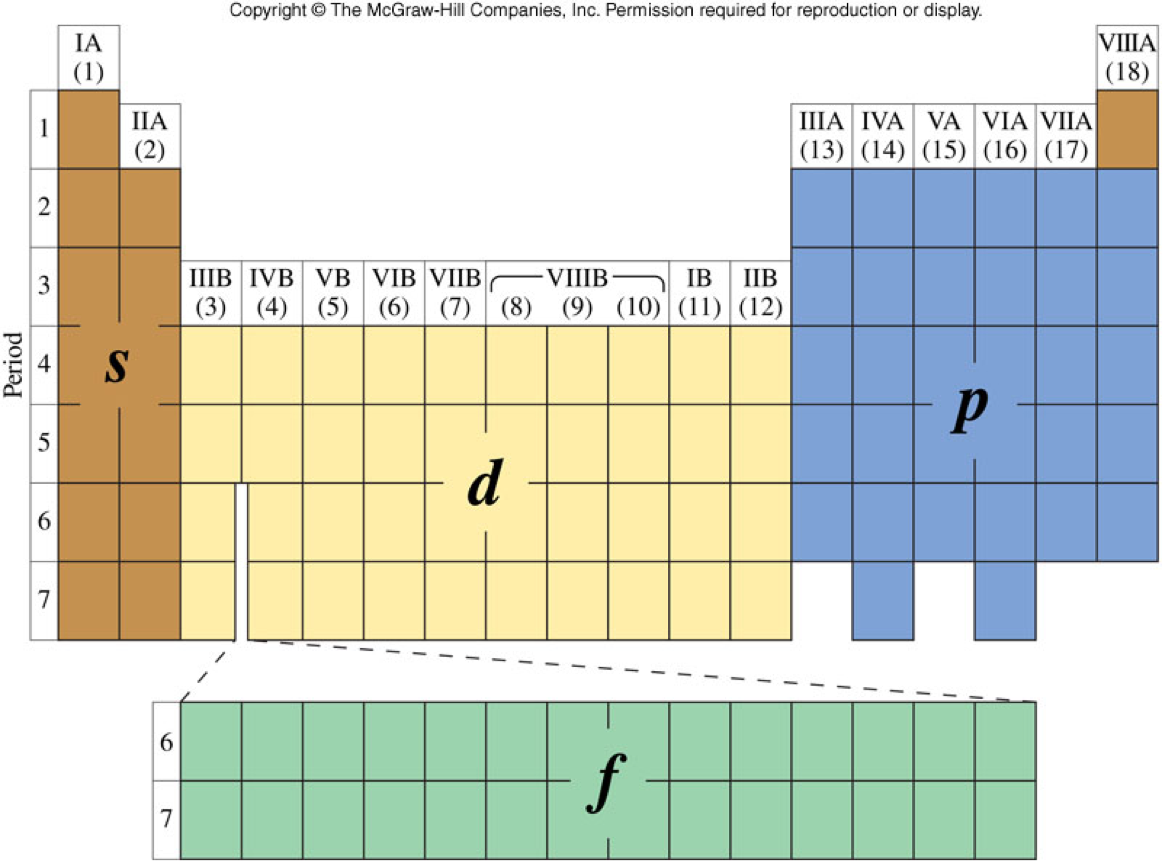
Valence Electrons for Main-Group Elements

• Valence level (shell)
  • Last-filled principal energy level
  • Highest energy level
  • Contains orbitals that are larger than orbitals in lower energy levels
• Valence electron
  • An electron that occupies the valence level
  • Elements in the same group have the same number of valence electrons
  • Example: Br – \( \chem{1s^22s^22p^63s^23p^64s^23d^{10}4p^5}\)

More on Valence Electrons

• Valence electrons
  • The Roman numeral group number (which is paired with an A or B).
  • The number of valence electrons is also equal to the number of s and p electrons in the valence level for any main-group element.
• Core electron
  • An electron in a principal energy level below the valence level
  • Inner electron

Abbreviated Electron Configuration

• Starts the electron configuration at the last noble gas before the element in question.
• Write down the noble gas in brackets, then fill in the rest of the electron configuration until you reach the element in question.
• Example:
  • Phosphorus (P) has 15 electrons. In the long notation, the electron configuration for P would be: \[ \chem{1s^22s^22p^63s^23p^3} \]
  • The abbreviated electron configuration for P would be: \[ \chem{[Ne]3s^23p^3} \]

Electron Configurations for Ions

• Ions form because atoms gain or lose electrons
  • Cations
    • Positively charged ions
    • Subtract the number of the charge from the total number of electrons
    • Move to the left the number of spaces equal to the charge on the periodic table
  • Anions
    • Negatively charged ion
    • Add the number of the charge to the total number of electrons
    • Move to the right the number of spaces equal to the charge on the periodic table

Periodic Trends of Atoms

• Valence electrons are the electrons that participate in chemical reactions because they are the farthest electrons from the nucleus.
• Because elements in the same group have the same number of valence electrons, elements in the same group have very similar reactivities.

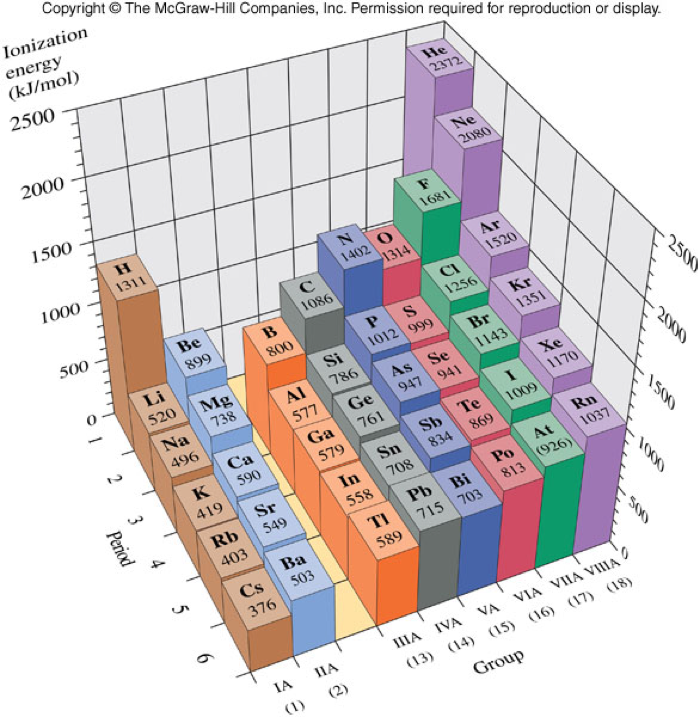
Ionization Energy

• Ionization Energy
  • A measure of the energy required to remove a valence electron from a gaseous atom to form a gaseous ion.
  • In general, atoms with low ionization energies do not bind their electrons very tightly, and are therefore, very reactive.
  • The general trend for ionization energy is for ionization energy to increase from bottom to top and from left to right across the periodic table.

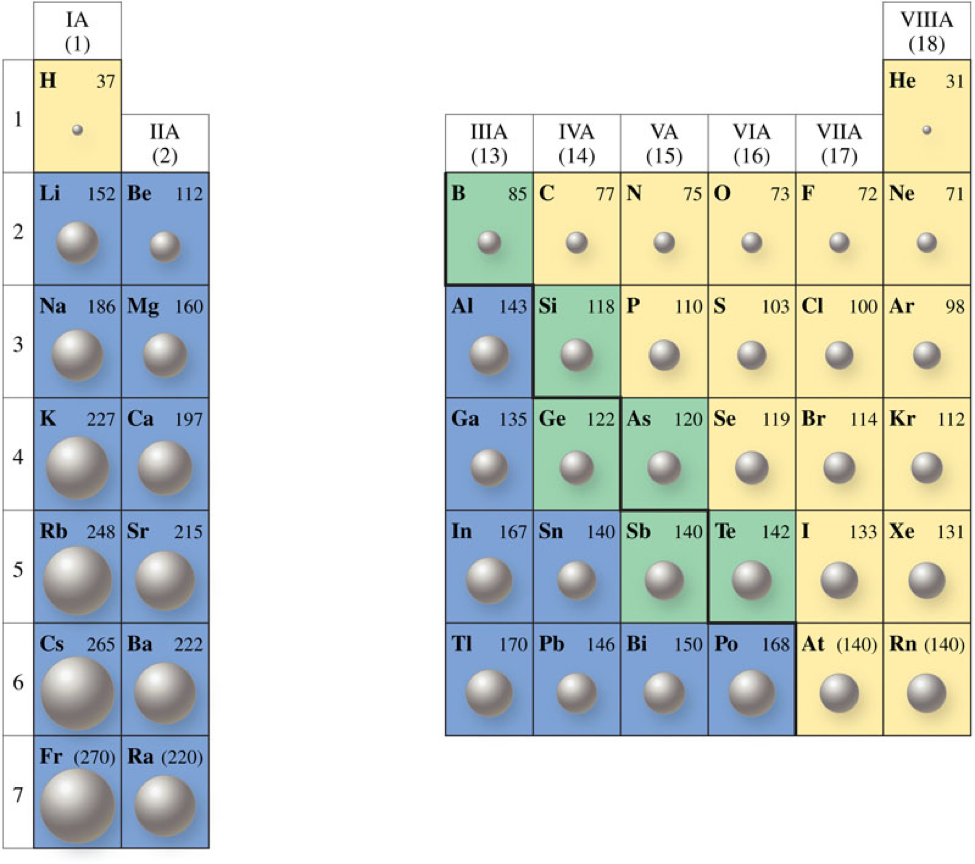
Atomic Size

• Atomic size is often described in terms of atomic radius.
  • Atomic radius is the distance from the center of the nucleus to the outer edge of the atom.

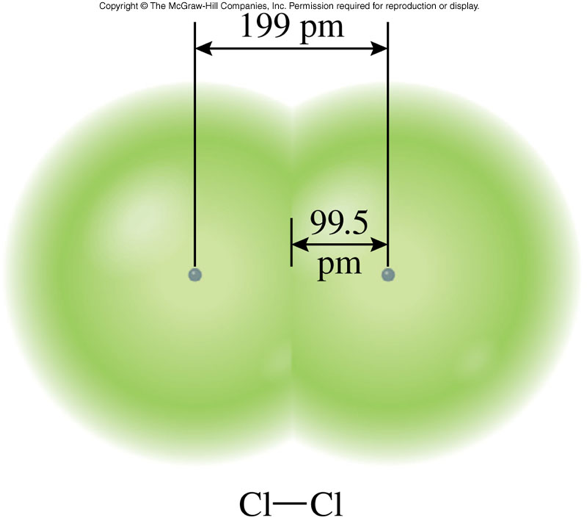
Trends in Atomic Size

• The general trend for atomic size (or radius) is for atomic size to increase from top to bottom and from right to left across the periodic table.

Ionic Size

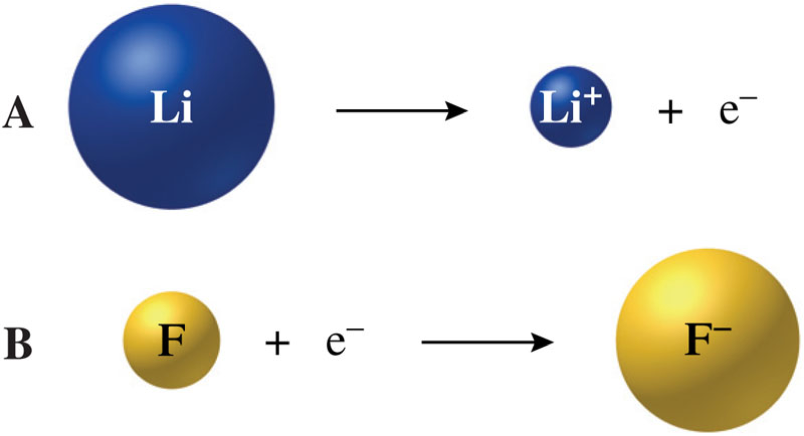
• Ionic size
  • Radius of an ion
  • Atoms change radius when they become ions
• The general trend for ionic size (or radius) is for ionic size to increase from top to bottom.
  • For cations, as the charge increases, the ionic size decreases.
  • For anions, as the charge increases in negativity, the ionic size increases.

Ionic Size

• For any isoelectronic series, as the number of protons increases, the ion size decreases.