Molecular Orbital Theory
Shaun Williams, PhD
Constructing Molecular Orbitals from Atomic Orbitals
- We typically use atomic orbitals (AOs) as a basis for constructing MOs
- LCAO-MO (linear combination of atomic orbitals) - we have seen LCAO before when we built our hybrid orbitals in the previous section.
- When they add in phase, we get constructive interference and lower energy bonding orbital
- When they add out of phase, we get destructive interference and a higher energy antibonding orbital
Sigma Bonding and Antibonding Combinations of an s and p Orbital
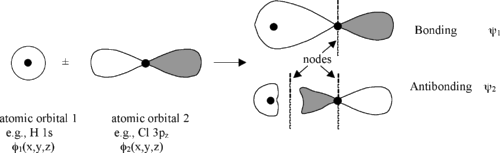
- Molecular orbitals are also called wavefunctions (\(\psi\))
- The atomic orbitals (also called basis functions) are labeled \(\phi\), for example \(\phi_{1s}\) and \(\phi_{3p_z}\) or simply as \(\phi_1\) and \(\phi_2\)
Orbitals in Molecules
- In principle, we need to solve the Schrödinger equation for all the orbitals in a molecule, and then fill them up with pairs of electrons as we do for the orbitals in atoms
- In practice, we are really interested only in the MOs that derive from the valence orbitals of the constituent atoms because these are the orbitals that are involved in bonding
- We are especially interested in the frontier orbitals (ie. the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO)
Other Orbitals
- Filled orbitals that are much lower in energy (ie. core orbitals) do not contribute to bonding
- Empty orbitals at higher energy likewise do not contribute to bonding
- These orbitals are important in photochemistry and spectroscopy which involve electronic transitions from occupied to empty orbitals
- Fluorescent dyes that stain the cells absorb light by promoting electrons in the HOMO to empty MOs and give off light when the electrons drop back down to their original energy levels.
Fluorescently Stained Endothelial Cells
Example of LCAO-MO
- We can construct two MOs (\(\psi_1\) and \(\psi_2\)) of the \(HCl\) molecule from two AOs \(\phi_1\) and \(\phi_2\)
- Mathematically we get \[ \Psi_1=c_1\phi_1 + c_2 \phi_2 \;\;\;\; \text{ and } \;\;\;\; \Psi_2=c_1\phi_1 - c_2\phi_2 \]
- The coefficients will be equal (or nearly equal) when the two AOs from which they are constructed are the same
- The coefficients will be unequal when there is an energy difference between the AOs
Nodes
- The wavefunctions \(\phi\) and \(\psi\) are amplitudes that related to the probability of finding the electron at some point in space.
- They have lobes with (+) and (-) signs, which are often indicated by shading or color
- Wherever the wavefunction changes sign there is a node
- Nodes in MOs result from destructive interference of (+) and (-) wavefunctions
- Generally, the more nodes, the higher the energy of the orbital
Nodal Structure of 2p and 3p Orbitals
- Shown below are the 2p and the 3p orbitals
- The 2p orbital has an angular node and no radial nodes
- The 3p orbital has an angular node and one radial node

Normalization
- We square the wavefunctions to get probabilities, which are always positive or zero
- If an electron is in \(\phi_1\), the probability of finding it at a point \(x,y,z\) is the square of \(\phi_1(x,y,z)\)
- The total probability does not change when we combine AOs to make MOs
- For a simple case \[ \Psi_1^2+\Psi_2^2 = \phi_1^2+\phi_2^2 \]
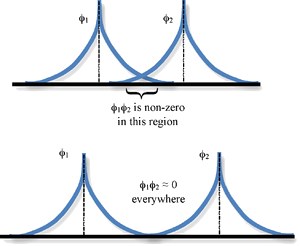
Overlap Integral
- The spatial overlap between two atomic orbitals is described by the overlap integral \(S\) \[ S_{12} = \int \phi_1^* \phi_2 d\tau \] where the integration is over all space (\(d\tau = dx\, dy\, dz\))
Graph of Orbital Overlap
Energies of Bonding and Antibonding MOs
- The energies of bonding and antibonding orbitals depend strongly on the distance between the atoms
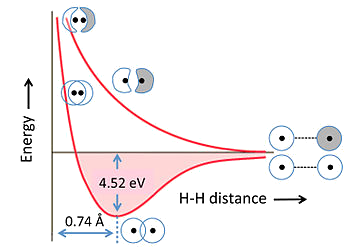
Equilibrium Bond Energy
- At equilibrium bond distance, the energies of the bonding and antibonding MO are lower and higher than the energies of the atomic basis orbitals
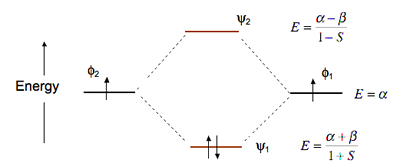
Energetics
- The energy of an electron in one of the atomic orbitals is \(\alpha\), the Coulomb integral \[ \alpha=\int \phi_1 \mathcal{H} \psi_1\, d\tau = \int \phi_2 \mathcal{H} \psi_2 \, d\tau \] where \(\mathcal{H}\) is the Hamiltonian operator
- \(\alpha\) is basically the ionization energy of an electron in the AOs
- The energy difference between an electron in the AOs and MOs is determined by the exchange integral \(\beta\) \[ \beta=\int \phi_1 \mathcal{H} \phi_2 \, d\tau \]
The Exchange Integral
- Calculating \(\beta\) is not straightforward for multi-electron molecules because we cannot solve the Schrödinger equation analytically for the wavefunction
- We can make some approximations however
- In the Hückel approximation, which can be used to obtain approximate solutions for \(\pi\) molecular orbitals in organic molecules, we simplify the math by taking \(S=0\) and setting \(\mathcal{H}=0\) for any p-orbitals that are not adjacent to each other
- The extended Hückel and other semi-empirical methods can be used to rapidly obtain relative orbital energies, approximate wavefunctions, and degeneracies of molecular orbitals
MO Wavefuctions
- We can get the coefficients \(c_1\) and \(c_2\) for the hydrogen molecule by applying the normalization criterion: \[ \Psi_1=\frac{\phi_1+\phi_2}{\sqrt{2}\left( 1+S \right)} \; \text{(for bonding orbital)} \] and \[ \Psi_2=\frac{\phi_1-\phi_2}{\sqrt{2}\left( 1-S \right)} \; \text{(for antibonding orbital)} \]
- When \(S\approx 0\), we can eliminate the \(1-S\) terms and both coefficients become \(\frac{1}{\sqrt{2}}\).
\(H_2\) Example
- The bonding MO of \(H_2\) is stabilized by an energy \(\frac{\beta}{1+S}\) and the antibonding MO is destabilized by \(\frac{\beta}{1-S}\)
- This means that the antibonding MO goes up in energy more than the bonding MO goes down
- This means the \(H_2\) (\(\psi_1^2\psi_2^0\)) is energetically more stable than two H atoms
- \(He_2\), however, with four electrons (\(\psi_1^2 \psi_2^2\)) is unstable relative to two He atoms
Bond Order
- In any MO diagram, the bond order can be calculated as \[ \frac{1}{2} \left( \text{bonding electrons} - \text{antibonding electrons} \right) \]
- For \(H_2\) the bond order is 1, and for \(He_2\) the bond order is zero.
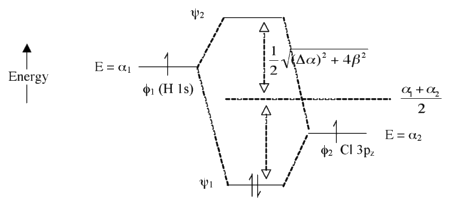
Heteronuclear Case (eg. \(HCl\)) - Polar Bonds
- The energy of an electron in the H \(1s\) orbital is higher than the electron in the chlorine \(3p_z\) orbital
- This results in a larger energy difference between the resulting MOs
- The bigger the electronegativity difference between AOs (the larger \(\Delta \alpha\) is) the more "\(\phi_2\) character" the bonding orbital has (ie. the more is resembles the Cl \(3p_z\) orbital in this case)
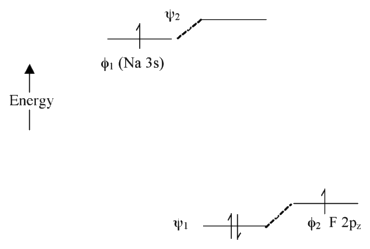
Extreme Case - Ionic Bonding \(NaF\): Very Large \(\Delta \alpha\)
- In this case, there is not much mixing between the AOs because their energies are far apart
- The two bonding electrons are localized on the F atom, so we can write the molecule as \(Na^+F^-\)
- Note that if we were to excite an electron from \(\psi_1\) to \(\psi_2\) using light, the resulting electron configuration would be (\(\psi_1^1\psi_2^1\)) and we would have \(Na^0F^0\) - this is called a charge transfer transition
Summary of MO Theory Thus Far
- Add and Subtract AO wavefunctions to make MOs. The total number of MOs equals the number of AO basis orbitals
- More nodes yields higher energy MO
- \(\text{bond order}=\frac{1}{2}\left( \text{bonding electrons} - \text{antibonding electrons} \right)\)
- Bond polarity emerges in the MO picture as orbital "character"
- AOs that are far apart in energy do not interact much when they combine to make MOs
Orbital Symmetry
- The MO picture get complicated when many valence AOs are involved
- We can simplify the problem a lot by noting (without proof here, take CHE 304!!) that orbitals of different symmetry with respect to the molecules do not interact.

Nodal Symmetry
- AOs must have the same nodal symmetry (as defined by the molecular symmetry operations) or their overlap is zero
- For example, in \(HCl\), the molecular symmetry (bonding) axis is z as shown below

Nonbonding Orbitals
- Because those two orbitals have different symmetries, the \(Cl\) \(3p_y\) orbital is nonbonding and doesn't interact with the \(H\) \(1s\).
- The same is true of the \(Cl\) \(3p_x\) orbital
- The \(p_x\) and \(p_y\) orbitals have \(\pi\) symmetry (nodal plane containing the bonding axis) and are labeled \(\pi_{nb}\) in the MO energy level diagram
- In contrast, the \(H\) \(1s\) and \(Cl\) \(3p_z\) orbitals both have \(\sigma\) symmetry
- Because these orbitals have the same symmetry (in the point group of the molecule), they can make the bonding and antibonding MO combinations
The MO Diagram of \(HCl\)
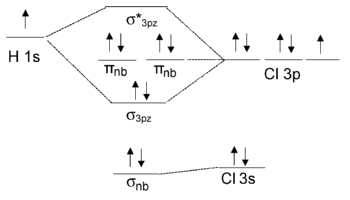
- Note that there is 1 bond and three pairs of nonbonding electrons
- The nonbonding orbitals are localized on the \(Cl\) atom
- This is the same are we get from the valence bond theory for \(HCl\)
Important Note on Axes
- The three dimensions are usually denoted as \(x,y,z\)
- We assign the bonding axis as \(z\) for the purpose of convenience
- There is no good reason for any individual s orbital to combine with a particular p orbital
- We define a bonding axis because it makes the descriptions of the types of bonds easier - \(\sigma\) bonds occur along the \(z\) axis, \(\pi\) bonds occur in the \(xz\) plane, and \(\delta\) bonds occur through the \(yz\) plane
- The origin is define as the central atom
- The \(y\) and \(z\) axes are define by the other two p orbitals or by being orthogonal to the bonding axis (same thing actually)
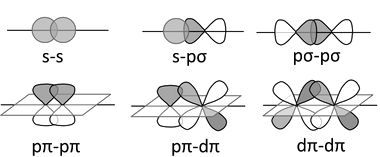
\(\sigma\), \(\pi\), and \(\delta\) Orbitals
- Inorganic compounds use \(s\), \(p\), and \(d\) orbitals (and more rarely \(f\) orbitals) to make bonding and antibonding combinations.
- These combinations result is \(\sigma\), \(\pi\), and \(\delta\) bonds (and antibonds)
- You are already familiar with \(\sigma\) and \(\pi\) bonding in organic chemistry
- In inorganic chemistry, \(\pi\) bonds can be made from \(p\) and/or \(d\) orbitals
- \(\delta\) bonds are more rare and occur by face-to-face overlap of \(d\) orbitals, as in \(\left[ Re_2Cl_8 \right]^{2-}\)
The Octachlorodirhenate(III) Anion
- In the octachlorodirhenate(III) anion, \(\left[Re_2Cl_8 \right]^{2-}\), there is a quadruple \(Re-Re\) bond
-3D-balls.png)
\(\sigma\) and \(\pi\) Bonding
\(\delta\) Bonding
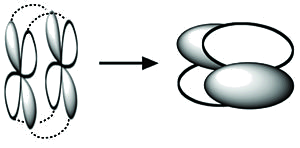
\(d\)-Orbitals and \(\sigma\) Bonds
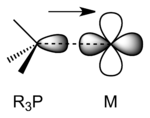
- Transition metal \(d\)-orbitals can also form \(\sigma\) bonds, typically with \(s-p\) hybrid orbitals of appropriate symmetry on ligands
- For example, phosphines (\(R_3P\)) are good \(\sigma\) donor in complexes with transition metals

\(p\pi-d\pi\) Bonding
- \(p\pi-d\pi\) bonding is also important in transition metal complexes
- In metal carbonyl complexes such as \(Ni(CO)_4\) and \(Mo(CO)_6\), there is sideways overlap between filled metal \(d\)-orbitals and the empty \(\pi\)-antibonding orbitals of the \(CO\) molecule.
- This interaction strengthens the metal-carbon bond but weakens the carbon-oxygen bond
- The \(C-O\) infrared stretching frequency is diagnostic of the strength of the bond and can be used to estimate the degree to which electrons are transferred from the metal \(d\)-orbital to the \(CO\) \(\pi\)-antibonding orbital
- This same kind of backbonding occurs with phosphine complexes, which have empty \(\pi\) orbitals, shown previously
Diatomic Molecules

- Valence bond theory fails for a number of second row diatomics, most famously for \(O_2\)
- Valence bond theory predicts doubly bonded molecule with four lone pairs
- \(O_2\) has a double bond but it has two unpaired electrons in the ground state which can be explained by the MO picture
MO Diagrams
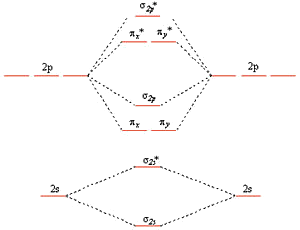
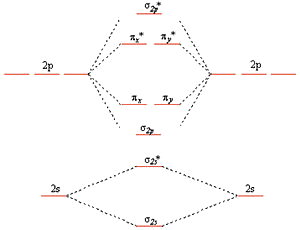
- The diagram on the left results from the mixing of the \(\sigma_{2s}\) and \(\sigma_{2p}\) MOs which are close in energy for \(Li_2\), \(Be_2\), \(B_2\), \(C_2\), and \(N_2\).
- This mixing pushes the \(\sigma_{2s}\) down in energy and the \(\sigma_{2p}\) up
Why No sp-orbital Mixing in \(O_2\) and \(F_2\)
- The energies in the diagrams on the previous slide are not to scale
- As we move across the second row, the added protons effect the 2s more than the 2p.
- As the energy difference between the s and p orbitals increases their interaction increases
- This results in less mixing
Orbital Energy Trends
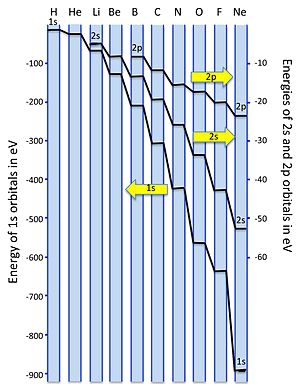
Orbital Filling
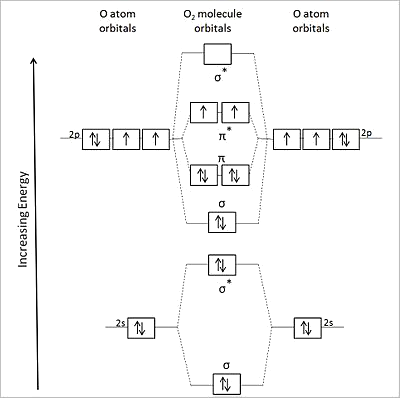
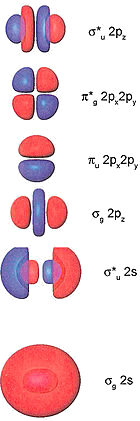
More Labels for MOs
- The symbols "g" and "u" in the orbital labels, which we only include in the case of centrosymmetric molecules
- They refer to the orbital symmetry with respect to inversion
- Gerade (g) orbitals are symmetric, meaning that inversion through the center leaves the orbital unchanged
- Ungerade (u) orbitals have signs that are reversed by the inversion process
- Because g and u orbitals have different symmetries, they have zero overlap with each other
Periodic Trends in \(\pi\) Bonding
Ethylene vs Silylene
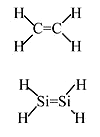
- Ethylene is stable and needs a catalyst to polymerize
- Silylene has never been isolated as it spontaneously polymerizes. This is due to the large core of Si atoms which inhibit sideways overlap of 3p orbitals (weak \(\pi\) bond)
Phosphorous vs Nitrogen
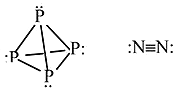
- Phosphorous cannot make \(\pi\) bonds with itself so it forms a tetrahedral molecule with substantial ring strain. This allotrope also undergoes spontaneous combustion in air
- Nitrogen can make \(\pi\) bonds with itself so it has a very strong triple bond and is relatively inert diatomic gas.
Silicone Polymer vs Acetone
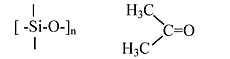
- Siloxanes - four single bonds to Si
- Acetone - a double bond between C and O
Three-Center Bonding
- Many of the problems we will solve with MO theory derive from the MO diagram of the \(H_2\) molecule, which is a case of two-center bonding
- The rest we will solve by analogy to the \(H_3^+\) ion, which introduces the concept of three-center bonding
- We can draw the \(H_3^+\) ion (and also \(H_3\) and \(H_3^-\)) in either a linear or triangular geometry
Walsh Correlation Diagram for \(H_3^+\)
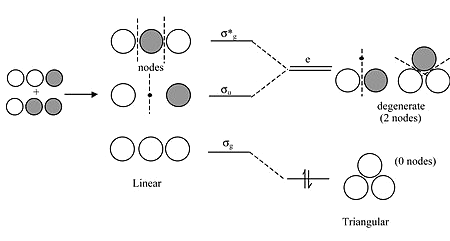
- For the linear form, the highest and lowest MOs are symmetric with respect to the inversion center in the molecule
- The central \(1s\) orbital has g symmetry, so by symmetry it has zero overall with the u combination of the two 1s orbitals on the ends - this makes the \(\sigma_u\) orbital a nonbonding orbital
Walsh Correlation Diagram for \(H_3^+\) Continued

- In the triangular form, the orbitals that derive from \(\sigma_u\) and \(\sigma_g^*\) become degenerate - they have identically the same energy by symmetry
- The term "e" means double degenerate ("t" means triply degenerate)
- No g and u because the triangular form does not have an inversion center
Walsh Correlation Diagram for \(H_3^+\) Final

- The triangular form is most stable because the two electrons in \(H_3^+\) have lower energy in the lowest orbital
- Bending the molecule creates a third bonding interaction between the \(1s\) orbitals on the ends
MO Diagram for \(XH_2\) (\(X=Be, B, C, \dots\))
- This is far more complicated due to the p orbitals on the central atom
- We can use symmetry factors to solve the problem
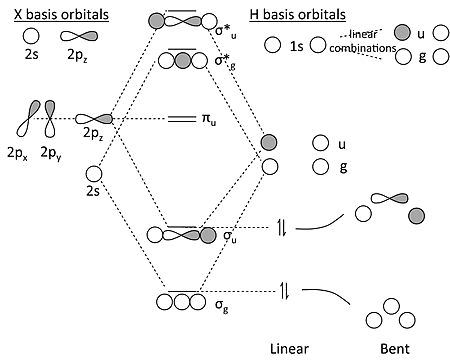
Key Points about the MO Diagram for \(XH_2\)

- The linear form has inversion symmetry, the \(2s\) and \(2p\) orbitals of the X atoms factor into three symmetry classes
- The two H \(1s\) orbitals make two linear combinations, one with \(\sigma_g\) symmetry and one with \(\sigma_u\) symmetry
Key Points about the MO Diagram for \(XH_2\) - More

- The \(\pi_u\) orbital must be non-bonding because there is no combination of the H \(1s\) orbitals that has \(\pi_u\) symmetry
- We make bonding and antibonding combinations of the \(\sigma_g\)'s and \(\sigma_u\)'s.
- The correlation diagram shows that the bent form should be less stable
Building Up the MOs of More Complex Molecules: \(NH_3\), \(P_4\)
- Let's try some more complicated molecules.
MO Diagram for \(NH_3\)
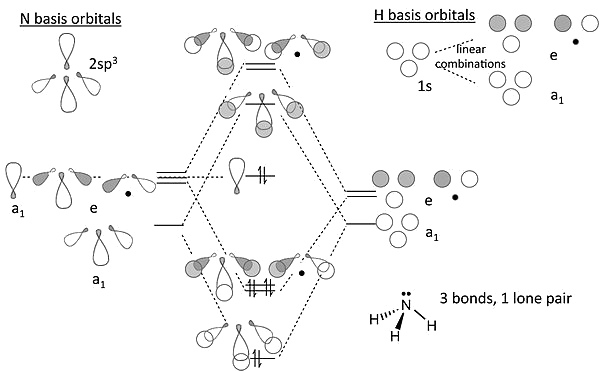
- Viewed end-on, a \(p\)-orbital or an \(sp_x\) hybrid looks just like an \(s\)-orbital so we can use the solutions we developed with \(s\)-orbitals for \(H_3^+\)
MO Diagram for \(NH_3\) - More

- We construct the \(sp^3\) hybrid orbitals of the nitrogen atom and orient them so that one is "up" and the other three form the triangular base
- These last three, by analogy to \(H_3^+\) transform as one totally symmetric ("\(a_1\)") and an e-symmetry pair. The "up" one is also \(a_1\)
MO Diagram for \(NH_3\) - Still More

- We can now make bonding and antibonding combinations between nitrogen orbitals and the H combinations of the same symmetry
\(P_4\) Molecule and \(P_4^{2+}\) Ion
- By analogy to \(NH_3\) we can construct the MO picture for one vertex of the \(P_4\) tetrahedron and then multiply the result by 4 to get the bonding picture for the molecule
- An important difference is that there is relatively little \(s-p\) hybridization in \(P_4\)
- The lone pair orbitals have more \(s\)-character and are lower in energy than the bonding orbitals
- Take away two electrons to make \(P_4^{2+}\)
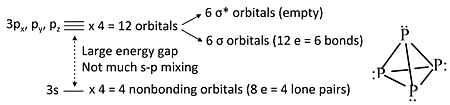
Homology of \(\sigma\) and \(\pi\) Orbitals in MO Diagrams
- The ozone molecule (and related 18 electron molecules that contain three non-H atoms, \(NO_2^-\) and allyl anion \([CH_2-CH-CH_2]^-\)) is an example of 3-center 4-electron \(\pi\)-bonding
- Our MO treatment of ozone is entirely analogous to the 4-electron \(H_3^-\) anion
MO Diagram of Ozone
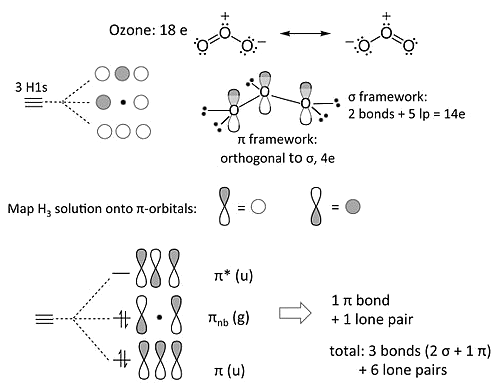
\(I_3^-\)
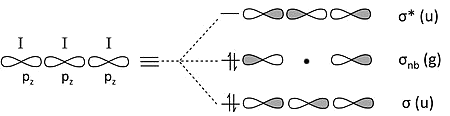
- This is analogous and seemingly more complicated case of 3-center 4-electron bonding
- We can simplify it by recalling two periodic trends
- The \(s-p\) orbital splitting is large, relative to the bond energy, after the second row of the periodic table. Therefore the \(5s\) orbital is low in energy and too contracted to make bonds with its neighbors
- \(\pi\)-overlap of \(5p\) orbitals is very weak, so the \(5p_x\) and \(5p_y\) orbitals will also be non-bonding
- This leaves only the three \(5p_z\) orbitals to make bonding / nonbonding / antibonding combinations
MO Diagram of \(I_3^-\)
- Our simplifications mean that our picture is much simpler
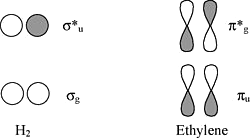
Chains and Rings of \(\pi\)-Conjugated Systems
- Viewed from the top or bottom, the ethylene \(\pi\)-orbitals look like \(H_2\) \(\sigma\) orbitals.
- We can map solutions from chains and rings of \(H\) atoms onto chains and rings of \(\pi\)-orbitals (as we did for the three-orbital case of \(O_3\))
Chains and Rings of 4 H atoms or \(\pi\)-Orbitals (\(H_4\) or Butadiene)
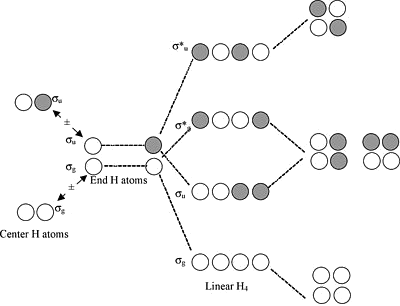
- In the linear form, the combination of AOs make a ladder of evenly spaced levels of alternating g-u-g-u. Each successive orbital has one more node
Chains and Rings of 4 H atoms or \(\pi\)-Orbitals (\(H_4\) or Butadiene) - More

- In the cyclic form, there is one non-degenerate orbital at the bottom, one at the top, and a ladder of doubly degenerate orbitals in between.
Benzene \(\pi\)-Orbitals
- We can get to the 6-atom chain by adding 2 atoms, one on each end, to the 4-atom chain
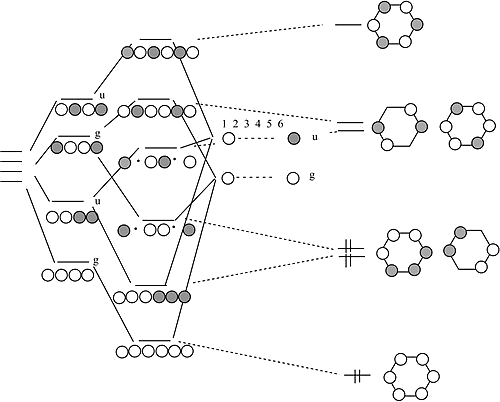
/