The Basics

Shaun Williams, PhD

The System and the Surroundings

• Universe - everything
• System - subset of the universe that is being studied
• Surroundings - every part of the universe that is not part of the system

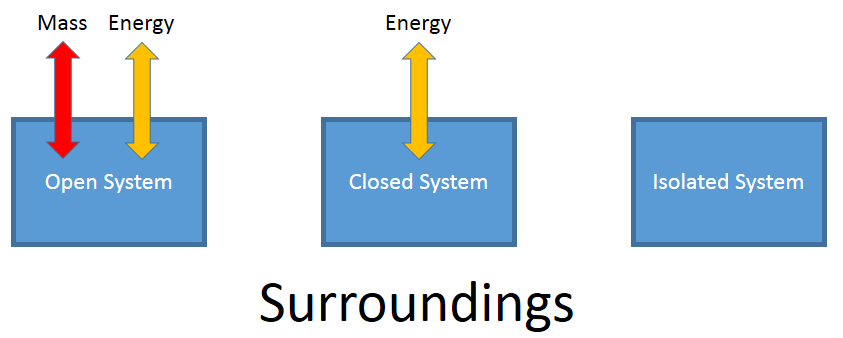
Types of Systems

• Open system - allows both mass and energy to transfer across its boundary
• Closed system - allows for energy to transfer across its boundary
• Isolated system - allows neither mass nor energy to transfer across its boundary

Types of Variables

• State variables - important variables that describe the system (pressure, temperature, volume)
• intensive variable - independent of the amount of substance present (such as temperature and color)
• extensive variable - dependent on the amount of substance present (such as volume and mass)

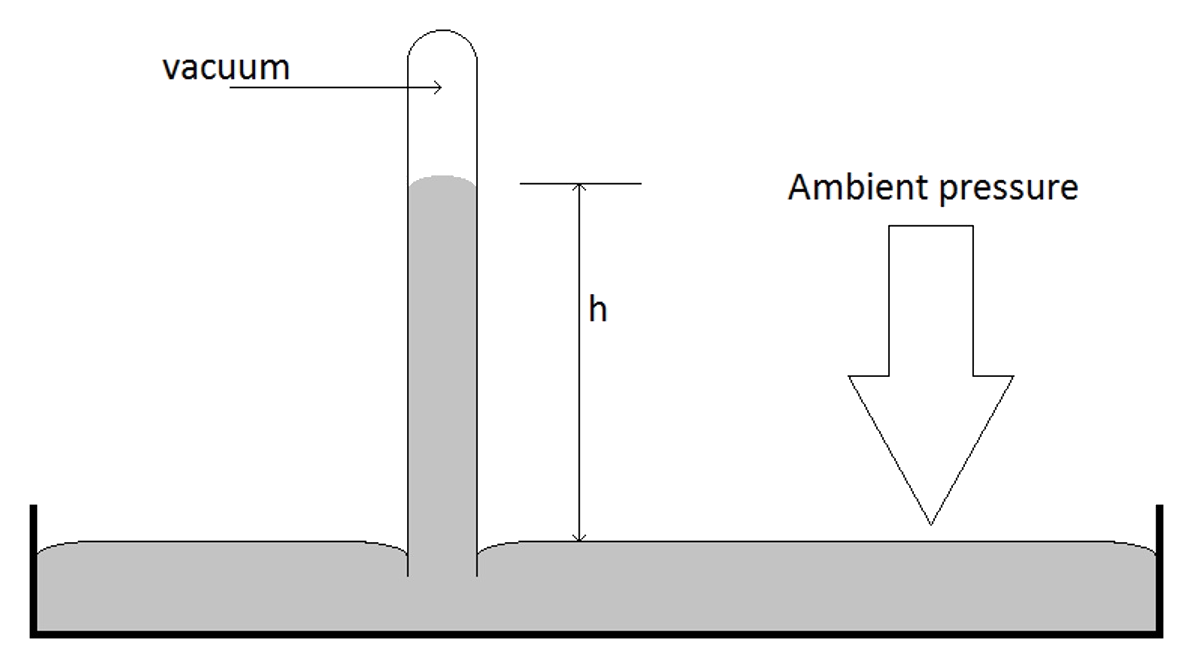
Pressure

• Pressure is a force being applied over a surface area
• Barometer is a basic device, developed by Evangelista Torricelli (1608-1647) to measure air pressure

Temperature

• Temperature is another major variable of the state of a system
• Various temperature scales exist
• G. Daniel Fahrenheit (1686-1736) developed the Fahrenheit temperature scale to use in his laboratory
• Anders Celsius (1700-1780) developed the Celsius temperature scale (originally called the centigrade scale)
• William Lord Kelvin (1824-1907) developed the absolute temperature scale

\[ y^\circ F = x^\circ C \left(\frac{9^\circ F}{5^\circ C}\right) + 32^\circ F \] \[ z\,K = x^\circ C \left(\frac{1\,K}{1^\circ C}\right) + 273.15\,K \]

The Zeroth Law of Thermodynamics

• Temperature is an important property in measuring energy flow in systems

If a system A is in thermal equilibrium with a system B, which is also in thermal equilibrium with system C, then systems A and C share a property called temperature.

Work and Energy

• Energy can flow in two forms: work and heat

Energy

• Energy can have two forms: potential and kinetic
• Potential energy is stored energy
• Kinetic energy is the energy of motion, \( E_{k}=\frac{1}{2}mv^2 \)

Work

• Work is the amount of energy expended to moving a mass against a resisting force

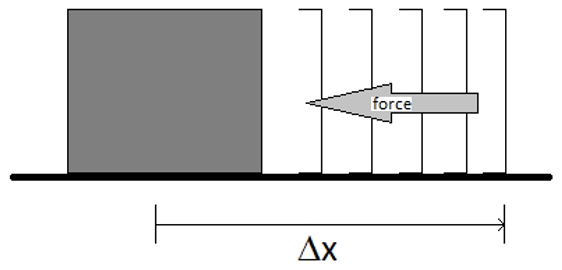
• For displacement work: \( w=-F\,\Delta x\)
• Work done by a gas expanding against an external pressure: \(dw = -P_{ext} \, dV\)

Work of a "Reversible" Expansion

• A reversible expansion is a limiting ideal behaviorts
• For a change to be reversible, there is no net force pushing a change, so in this case: \( P_{int}=P_{ext}=P\)

Example 1.1

Consider \(1.00\, mol\) of an ideal gas, expanding isothermally at \(273\, K\), from an initial volume of \(11.2\, L\) to a final volume of \(22.4\, L\). What is the final pressure of the gas? Calculate the work of the expansion if it occurs

1. against a constant external pressure equal to the final pressure you have calculated.
2. reversibly.