Putting the First Law to Work

Shaun Williams, PhD

Total and Exact Differentials

We now know that \(C_V\equiv \left(\frac{\partial U}{\partial T}\right)_V\)
This suggests that \( U\) is very dependent on \( V\) and \( T\)
This suggests that to change \( U\) we can change these variables
This gives us a total differential \[ dU = \left(\frac{\partial U}{\partial V}\right)_T dV + \left(\frac{\partial U}{\partial T}\right)_V dT\]
This means that \[ \Delta U = \int_{V_1}^{V_2} \left(\frac{\partial U}{\partial V}\right)_T dV + \int_{T_1}^{T_2} \left(\frac{\partial U}{\partial T}\right)_V dT \]

Exact Differentials

Let's say we have a differential \[ df(x,y) = P\,dx + Q\,dy \]
If these variable obey the Euler Relation \[ \left(\frac{\partial P}{\partial y}\right)_x = \left(\frac{\partial Q}{\partial x}\right)_y \] then that differential will be an exact differential
We can illustrate this with the ideal gas law \[ P(V,T) = \frac{RT}{V} \]
The differentils of all the state functions will be exact.

Compressivity and Expansivity

Isothermal Compressibility (\(\kappa_T\))

It is important that we understand how compressible substances are
To quantify how compressible substances are we can look at the fractional differential change in volume due to a change in pressure \[ \kappa_T \equiv -\frac{1}{V} \left(\frac{\partial V}{\partial P}\right)_T \]

Isobaric Thermal Expansivity (\(\alpha\))

It is also important to understand how the volume of a substance responds to temperature
To quantify this, we define the isobaric thermal expansivity (sometimes called the expansion coefficient) \[ \alpha \equiv \frac{1}{V} \left(\frac{\partial V}{\partial T}\right)_P \]

Partial Derivatives: The Reciprocal Rule

Consider a function \( F\) of three variables \(x\), \(y\), and \(z\) such that we can write \( F(x,y,z)=0 \)
This means that we can specify the system by knowning two of the three variables, or \[ dz = \left(\frac{\partial z}{\partial x}\right)_y dx + \left(\frac{\partial z}{\partial y}\right)_x dy \text{ and } dy = \left(\frac{\partial y}{\partial x}\right)_z dx + \left(\frac{\partial y}{\partial z}\right)_x dz \]
After a lot of calculus we find that \[ 1=\left(\frac{\partial z}{\partial y}\right)_x \left(\frac{\partial y}{\partial z}\right)_x \text{ or } \left(\frac{\partial z}{\partial y}\right)_x = \frac{1}{\left(\frac{\partial y}{\partial z}\right)_x}\]

Partial Derivatives: The Cyclic Permutation Rule

Along similar lines to the last we, we can generate a very useful partial differential relationship

\[ \left(\frac{\partial z}{\partial x}\right)_y = -\left(\frac{\partial z}{\partial y}\right)_x \left(\frac{\partial y}{\partial x}\right)_z \]

Example 4.1

Derive an expression for \[ \frac{\alpha}{\kappa_T} \] in terms of derivatives of thermodynamic functions using out partial derivative relations.

The Joule Experiment

\[ dU = \left(\frac{\partial U}{\partial V}\right)_T dV + \left(\frac{\partial U}{\partial T}\right)_V dT \]

The second partial derivative is \(C_V\) \[ dU = \left(\frac{\partial U}{\partial V}\right)_T dV + C_V\, dT \]
What is the first term? Internal pressure \[ \pi_T = \left(\frac{\partial U}{\partial V}\right)_T \]

Measuring the Internal Pressure

James Prescott Joule (1818-1889) set out to measure the internal pressure

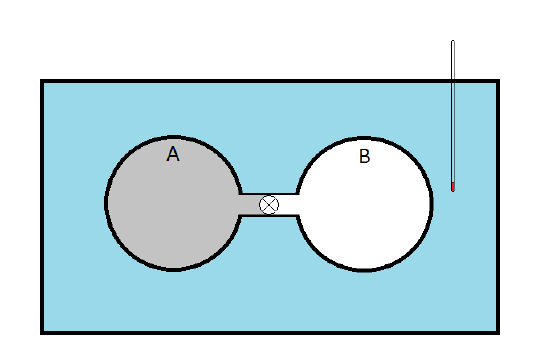
Two copper spheres, A and B, connected by a stopcock emmersed in a tank of water containing a thermometer. Sphere A is filled with a sample of gas while sphere B is evacuated.

A has a sample gas while B is evacuated

The Experiment

When the stopcock is opened, the gas expands into sphere B so \(\Delta V>0\)
Since B originally had a vacuum, this expansion is done against no external pressure so \(P_{ext}=0\,\therefore\, dw=-P_{ext}\,dV=0\)
We know that \(dU=dq+dw\) and that \(dU=\pi_T\,dV + C_V\,dT\) so \[ \pi_T\,dV + C_V\, dT = dq + dw = dq \]
Joule observed no temperature change in the water so he concluded that \(dq=0\) and \(dT=0\)
Since \(dV>0\) (the gas is expanding), Joule concluded that \(\pi_T=0\)
In truth, \(dT\ne 0\), but it was too small for Joule to detect it

\[ \pi_T=\left(\frac{\partial U}{\partial V}\right)_T = T\left(\frac{\partial P}{\partial T}\right)_V-P \]

Example 4.2: Internal Pressure of an Ideal Gas

What is the internal pressure, \(\pi_T\), of an ideal gas?

\[ \left(\frac{\partial U}{\partial V}\right)_T = T\left(\frac{\partial P}{\partial T}\right)_V-P \]

\[ PV_m=RT \]

Example 4.3: Internal Pressure of a van der Waals Gas

What is the internal pressure, \(\pi_T\), of a van der Waals gas?

\[ \left(\frac{\partial U}{\partial V}\right)_T = T\left(\frac{\partial P}{\partial T}\right)_V-P \]

\[ P=\frac{RT}{V_m-b} - \frac{a}{V_m^2} \]

The Joule-Thomson Effect

In 1852, Joule Began working with William Thomson (who would later become Lord Kelvin)

The Joule-Thomson Experiment

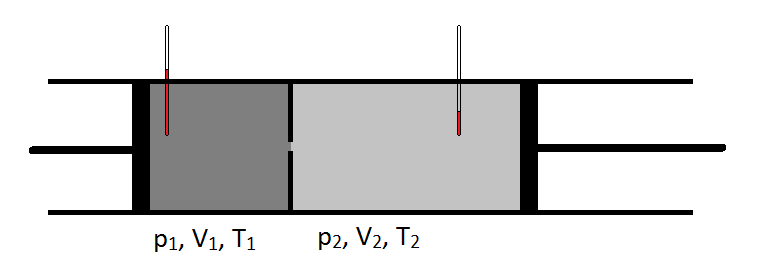
A depiction of the apparatus described on this slide.

Gas is pumped into the left side of a lead pipe at a constant rate
The pipe has a constriction in it so that the pressure in the left chamber is higher than the right chamber.
The temperature is monitored in each chamber.

The Joule-Thomson Coefficient

Not all gases cool as they expand from high pressure to low pressure
The sign of \(\Delta T\) can be determined by measuring the Joule-Thomson coefficient \[ \mu_{JT}\equiv \left(\frac{\partial T}{\partial P}\right)_H \]

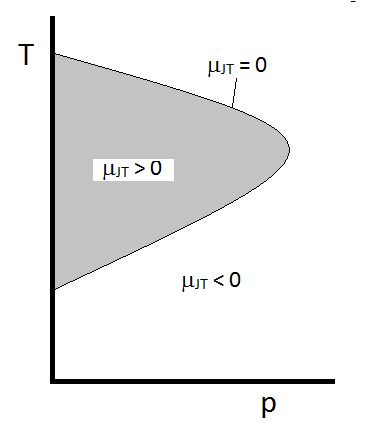
A plot of temperature versus pressure. The is a region at moderate temperature where the Joule-Thomson Coefficient is positive. Elsewhere it is negative.

Working to Make \(\mu_{JT}\) Measurable

We can develop an equation for calculating \(\mu_{JT}\) in terms of measurable quantities. But first

\[ dH \equiv \left(\frac{\partial H}{\partial P}\right)_TdP + \left(\frac{\partial H}{\partial T}\right)_PdT \] We will show later that \[ \left(\frac{\partial H}{\partial P}\right)_TdP = -T\left(\frac{\partial V}{\partial T}\right)_P+V \] The second term of which can be written in terms of the isobaric thermal expansivity \[ \left(\frac{\partial H}{\partial P}\right)_TdP = -TV\alpha +V = V\left(1-T\alpha\right) \]

More Derivation

\[ dH \equiv \left(\frac{\partial H}{\partial P}\right)_TdP + \left(\frac{\partial H}{\partial T}\right)_PdT \] Divide each side by \(dP\) and constrain to constant \(H\) \[ \left. \frac{dH}{dP}\right|_H = \left(\frac{\partial H}{\partial P}\right)_T\,\left.\frac{dP}{dP}\right|_H + \left(\frac{\partial H}{\partial T}\right)_P\,\left.\frac{dT}{dP}\right|_H \] This can be simplified \[ 0 = \left(\frac{\partial H}{\partial P}\right)_T\,\left(1\right) + \left(\frac{\partial H}{\partial T}\right)_P\,\left(\frac{\partial T}{\partial P}\right)_H \] \[ 0 = V \left(1-T\alpha\right) + \left(\frac{\partial H}{\partial T}\right)_P\,\left(\frac{\partial T}{\partial P}\right)_H \]

Completing the Derivation

\[ 0 = V \left(1-T\alpha\right) + \left(\frac{\partial H}{\partial T}\right)_P\,\left(\frac{\partial T}{\partial P}\right)_H \] We can use out definitions of \( C_P=\left(\frac{\partial H}{\partial T}\right)_P \) and \( \mu_{JT}=\left(\frac{\partial T}{\partial P}\right)_H \) \[ 0 = V \left(1-T\alpha\right) + C_P\mu_{JT} \] This can be solved to find that \[ \mu_{JT} = \frac{V\left(T\alpha -1\right)}{C_P} = \frac{V}{C_P}\left(T\alpha-1\right) \]

Useful Definitions and Relationships

Heat Capacities \[ C_V\equiv \left(\frac{\partial U}{\partial T}\right)_V \;\text{ and }\; C_P\equiv \left(\frac{\partial H}{\partial T}\right)_P \]
Coefficient of Thermal Expansion \[ \alpha \equiv \frac{1}{V}\left(\frac{\partial V}{\partial T}\right)_P \Rightarrow \left(\frac{\partial V}{\partial T}\right)_P = V\alpha\]

More Definitions and Relations

Isothermal Compressibility \[ \kappa_T \equiv -\frac{1}{V}\left(\frac{\partial V}{\partial P}\right)_T \Rightarrow \left(\frac{\partial V}{\partial P}\right)_T = -V\kappa_T \]
We have also seen that \[ \begin{eqnarray} \frac{\alpha}{\kappa_T} &=& \left(\frac{\partial P}{\partial T}\right)_V \\ \left(\frac{\partial U}{\partial V}\right)_T &=& T\left(\frac{\partial P}{\partial T}\right)_V-P \\ \left(\frac{\partial H}{\partial P}\right)_T &=& -T\left(\frac{\partial V}{\partial T}\right)_P+V \end{eqnarray} \]

Example 4.4

Derive an expression for \(\left(\frac{\partial H}{\partial V}\right)_T\) in terms of measurable quantities.

Example 4.5

Calculate \(\Delta H\) for the isothermal compression of ethanol which will decrease the molar volume by \(0.010\bfrac{L}{mol}\) at \(300K\). (For ethanol, \(\alpha=1.1\times 10^{-3}K^{-1}\) and \(\kappa_T=7.9\times 10^{-5}atm^{-1}\)).