Lecture 13
Acids and Bases
Shaun Williams, PhD
What Are Acids and Bases?
Arrhenius Model
- Arrhenius Model Acids and Bases
- Proposed by Svante Arrhenius in late 1800s
- An acid in aqueous solution produces hydrogen ions, \(\chem{H^+}\) \[ \chem{HCl(g) \xrightarrow{H_2O} H^+(aq)+Cl^-(aq)} \]
- A base in aqueous solution produces hydroxide ions, \(\chem{OH^-}\) \[ \chem{NaOH(s) \xrightarrow{H_2O} Na^+(aq)+OH^-(aq)} \]
- Also explains neutralization of acids and bases; when \(\chem{H^+}\) reacts with \(\chem{OH^-}\), water is formed \[ \chem{H^+(aq)+OH^-(aq)\rightarrow H_2O(l)} \]
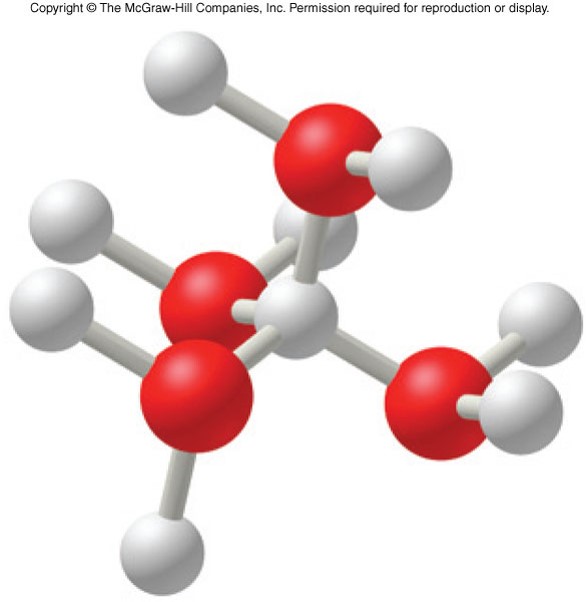
Hydronium Ion
- A fundamental problem with the Arrhenius model is the treatment of the behavior of the hydrogen ion, \(\chem{H^+}\)
- Hydrogen ions are better represented as hydronium ions, \(\chem{H_3O^+}\), in solution
Brønsted-Lowry Theory
- An acid is any substance that can donate an \(\chem{H^+}\) ion to another substance
- A base is any substance that can accept an \(\chem{H^+}\) ion from another substance
- Inclusive of all Arrhenius acids and bases
Conjugate Acid-Base Pairs
- When an acid donates an \(\chem{H^+}\) to a base, the two products differ from the reactants by one \(\chem{H^+}\) ion.
- Conjugate acid - The product that forms as a result of gaining an \(\chem{H^+}\) ion
- Conjugate base - The product that forms as a result of losing an \(\chem{H^+}\) ion
\[ \underbrace{\chem{HCl(g)}}_{\text{acid}} + \underbrace{\chem{H_2O(l)}}_{\text{base}} \rightarrow \underbrace{\chem{H_3O^+(aq)}}_{\text{ conjugate acid}} + \underbrace{\chem{Cl^-(aq)}}_{\text{conjugate base}} \]
Amphoteric Substances
- A substance that can act as either an acid or a base
- Water is the most common amphoteric substance. Another common amphoteric substance is the bicarbonate ion, \(\chem{HCO_3^-}\): \[ \underbrace{\chem{HCO_3^-(aq)}}_{\text{acid}} + \underbrace{\chem{OH^-(aq)}}_{\text{base}} \rightarrow \underbrace{\chem{CO_3^{2-}(aq)}}_{\text{conjugate base}} + \underbrace{\chem{H_2O(l)}}_{\text{conjugate acid}} \] \[ \underbrace{\chem{HCO_3^-(aq)}}_{\text{base}} + \underbrace{\chem{H_3O^+(aq)}}_{\text{acid}} \rightarrow \underbrace{\chem{H_2CO_3(aq)}}_{\text{conjugate acid}} + \underbrace{\chem{H_2O(l)}}_{\text{conjugate base}} \]
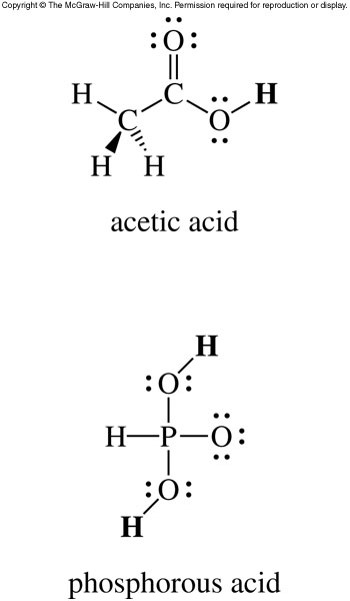
Acidic Hydrogen Atoms
- If an acid has more than one hydrogen atom, we need to determine which hydrogen atoms are acidic.
- Typically, in oxoacids, any hydrogen atoms bonded to oxygen atoms are acidic.
Strong and Weak Acids and Bases
Strong Acids and Bases
- An acid or a base that is a strong electrolyte and completely ionizes or dissociates in water
- Strong acid examples:
- \(\chem{HCl(aq)}\)
- \(\chem{H_2SO_4(aq)}\)
- \(\chem{HNO_3(aq)}\)
- Strong base examples:
- \(\chem{KOH(aq)}\)
- \(\chem{Ca(OH)_2(aq)}\)
- Strong acid examples:
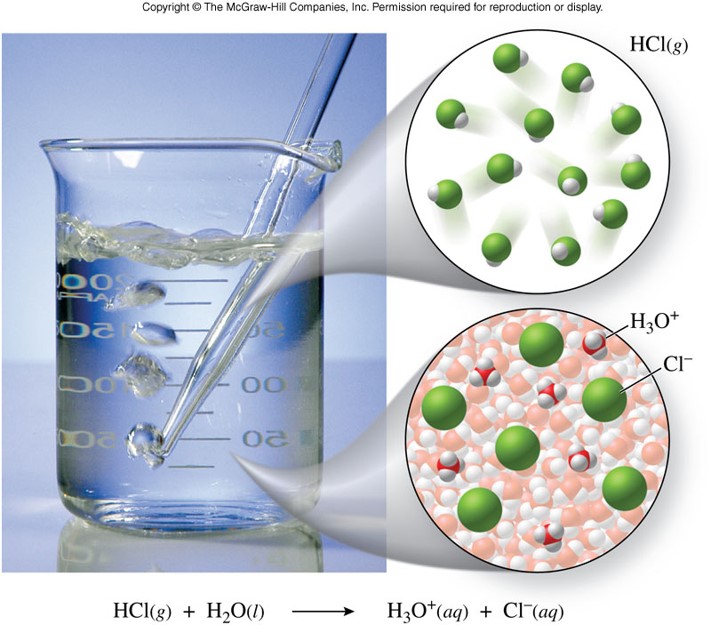
\(\chem{HCl}\) - Example of a Strong Acid
\[ \chem{HCl(aq)+H_2O(l) \rightarrow H_3O^+(aq)+Cl^-(aq)} \]
Common Strong Acids
| Formula | Name |
|---|---|
| \(\chem{HCl}\) | hydrochloric acid |
| \(\chem{HBr}\) | hydrobromic acid |
| \(\chem{HI}\) | hydroiodic acid |
| \(\chem{HNO_3}\) | nitric acid |
| \(\chem{HClO_3}\) | chloric acid |
| \(\chem{HClO_4}\) | perchloric acid |
| \(\chem{H_2SO_4}\) | sulfuric acid |
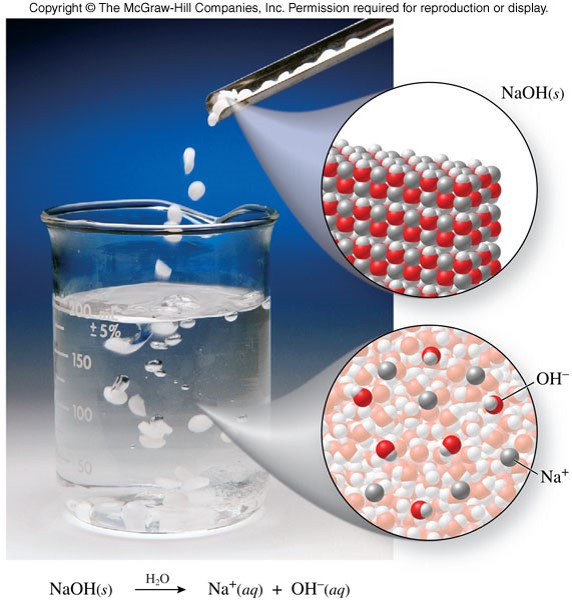
\(\chem{NaOH}\) - Example of a Strong Base
Common Strong Bases
| Formula | Name |
|---|---|
| \(\chem{LiOH}\) | lithium hydroxide |
| \(\chem{NaOH}\) | sodium hydroxide |
| \(\chem{KOH}\) | potassium hydroxide |
| \(\chem{Mg(OH)_2}\) | magnesium hydroxide |
| \(\chem{Ca(OH)_2}\) | calcium hydroxide |
| \(\chem{Ba(OH)_2}\) | barium hydroxide |
Weak Acids and Bases
- An acid or base that is a weak electrolyte and therefore, only partially ionizes in water
- If an acid or base is not strong, then it is weak.
\(\chem{HC_2H_3O_2}\) - Example of a Weak Acid
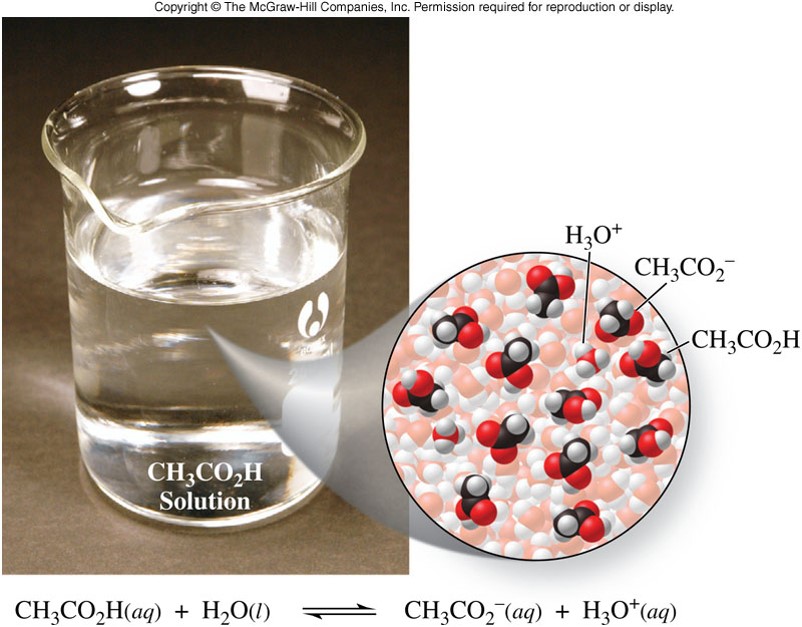
\(\chem{NH_3}\) - Example of a Weak Base

Some Common Weak Acids
| Formula | Name | Occurance |
|---|---|---|
| \(\chem{HC_2H_3O_2}\) | Acetic acid | Vinegar, sour wine |
| \(\chem{H_2CO_3}\) | Carbonic acid | Soda, blood |
| \(\chem{H_3C_6H_5O_7}\) | Citric acid | Fruit, soda |
| \(\chem{HF}\) | Hydrofluoric acid | Glass etching |
| \(\chem{HOCl}\) | Hypochlorous acid | Sanitize pool and drinking water |
| \(\chem{HC_3H_5O_3}\) | Lactic acid | Milk |
| \(\chem{HC_4H_4O_5}\) | Malic acid | Fruit |
| \(\chem{H_2C_2O_4}\) | Oxalic acid | Nuts, cocoa, parsley |
| \(\chem{H_3PO_4}\) | Phosphoric acid | Soda, blood |
| \(\chem{H_2C_4H_4O_6}\) | Tartaric acid | Candy, wine, grapes |
Some Common Weak Base
| Formula | Name | Occurance |
|---|---|---|
| \(\chem{NH_3}\) | Ammonia | Glass cleaners |
| \(\chem{CaCO_3}\) | Calcium carbonate | Antacids, minerals |
| \(\chem{Ca(ClO)_2}\) | Calcium hypochlorite | Chlorine source for swimming pools |
| \(\chem{CH_3NH_2}\) | Methylamine | Herring brine |
| \(\chem{(CH_3)_3N}\) | Trimethylamine | Rotting fish |
Relative Strengths of Weak Acids
- Acid strength depends on the relative number of acid molecules that ionize when dissolved in water – the degree of ionization.
- Remember that \(K_{eq}\) describes the relative amounts of products over reactants.
- If the value of \(K_{eq}\) is larger, then more products exist at equilibrium and the acid has a larger percentage of molecules which have been ionized.
Acid Ionization Constants
- The acid ionization constant, \(K_a\), describes the equilibrium that forms when an acid reacts with water.
- The larger the \(K_a\) value, the stronger the acid.
- When using \(K_a\) values to determine the strengths of conjugate acids and bases, use this rule of thumb:
- The stronger the acid, the weaker the conjugate base.
Weak Acids and \(K_a\) Values
| Acid | \(K_a\) | Conjugate Base | ||
|---|---|---|---|---|
| Strongest Acids | \(\chem{HF}\) | \(6.3 \times 10^{-4}\) | \(\chem{F^-}\) | Weakest Bases |
| \(\chem{HNO_2}\) | \(5.6 \times 10^{-4}\) | \(\chem{NO_2^-}\) | ||
| \(\chem{HCO_2H}\) | \(1.8 \times 10^{-4}\) | \(\chem{HCO_2^-}\) | ||
| \(\chem{HC_2H_3O_2}\) | \(1.8 \times 10^{-5}\) | \(\chem{C_2H_3O_2^-}\) | ||
| \(\chem{HOCl}\) | \(4.0 \times 10^{-8}\) | \(\chem{OCl^-}\) | ||
| \(\chem{NH_4^+}\) | \(5.6 \times 10^{-10}\) | \(\chem{NH_3}\) | ||
| Weakest Acids | \(\chem{HCN}\) | \(6.2 \times 10^{-10}\) | \(\chem{CN^-}\) | Strongest Bases |
Acidic Hydrogen Atoms
- An acid that contains more than one acidic hydrogen and can thus donate more than one \(\chem{H^+}\) ion
- The acid donates one \(\chem{H^+}\) ion at a time in steps
- The \(K_a\) values for polyprotic acids are often labeled to indicate the particular step in the overall ionization process (\(K_{a1}\), \(K_{a2}\), \(K_{a3}\), etc.)
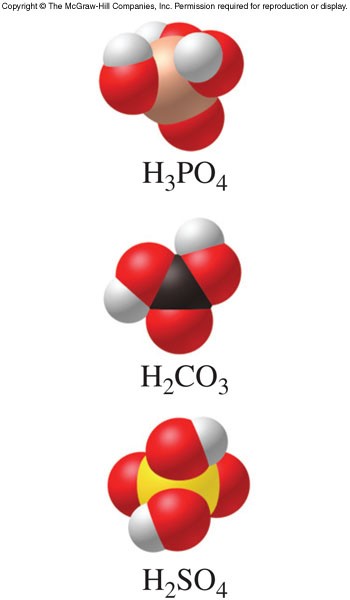
\(K_a\) for Polyprotic Acids
| Name | Formula | \(K_{a1}\) | \(K_{a2}\) | \(K_{a3}\) |
|---|---|---|---|---|
| Carbonic acid | \(\chem{H_2CO_3}\) | \(4.5 \times 10^{-7}\) | \(4.7 \times 10^{-11}\) | \(\) |
| Citric acid | \(\chem{H_3C_6H_5O_7}\) | \(7.4 \times 10^{-4}\) | \(1.7 \times 10^{-5}\) | \(4.0 \times 10^{-7}\) |
| Hydrosulfuric acid | \(\chem{H_2S}\) | \(8.9 \times 10^{-8}\) | \(1.0 \times 10^{-19}\) | \(\) |
| Oxalic acid | \(\chem{H_2C_2O_4}\) | \(5.6 \times 10^{-2}\) | \(1.5 \times 10^{-4}\) | \(\) |
| Phosphoric acid | \(\chem{H_3PO_4}\) | \(6.9 \times 10^{-3}\) | \(6.2 \times 10^{-8}\) | \(4.8 \times 10^{-13}\) |
| Sulfuric acid | \(\chem{H_2SO_4}\) | Strong | \(1.0 \times 10^{-2}\) | \(\) |
| Tartaric acid | \(\chem{H_2C_4H_4O_6}\) | \(1.0 \times 10^{-3}\) | \(4.3 \times 10^{-5}\) | \(\) |
Acidic, Basic, and Neutral Solutions
- Acidic solution
- The \(\chem{H_3O^+}\) ion concentration is greater than the \(\chem{OH^-}\) ion concentration.
- Basic solution
- The \(\chem{OH^-}\) ion concentration is greater than the \(\chem{H_3O^+}\) ion concentration.
- Neutral solution
- Equal concentrations of \(\chem{OH^-}\) and \(\chem{H_3O^+}\)
- Neither acidic nor basic
Ion-Product Constant of Water
- Water reacts with itself in a process called self-ionization, in which an \(\chem{H^+}\) ion is transferred from one water molecule to another: \[ \chem{H_2O(l) + H_2O(l) \rightleftharpoons OH^-(aq) + H_3O^+(aq)} \]
- The equilibrium constant for this process, called the ion-product constant of water, \(K_w\), is: \[ K_w = \left[ \chem{OH^-}\right] \left[ \chem{H_3O^+} \right] = 1.0 \times 10^{-14} \, \text{(at }25^\circ\text{ C)} \] and in pure water, the concentrations would be equal, so: \[ \left[\chem{OH^-}\right] = \left[ \chem{H_3O^+} \right] = 1.0 \times 10^{-7} \]
Definitions of Neutral, Acidic, and Basic Aqueous Solutions
| Type of solution | Relative Concentration | \(\chem{ \left[ H_3O^+ \right]}\) | \(\chem{ \left[ OH^- \right]}\) | \(K_w\) |
|---|---|---|---|---|
| Neutral | \(\chem{ \left[ H_3O^+ \right] = \left[ OH^- \right] }\) | \(1.0\times 10^{-7}\) | \(1.0\times 10^{-7}\) | \(1.0\times 10^{-14}\) |
| Acidic | \(\chem{ \left[ H_3O^+ \right] \gt \left[ OH^- \right] }\) | \(\gt 1.0\times 10^{-7}\) | \(\lt 1.0\times 10^{-7}\) | \(1.0\times 10^{-14}\) |
| Basic | \(\chem{ \left[ H_3O^+ \right] \lt \left[ OH^- \right] }\) | \(\lt 1.0\times 10^{-7}\) | \(\gt 1.0\times 10^{-7}\) | \(1.0\times 10^{-14}\) |
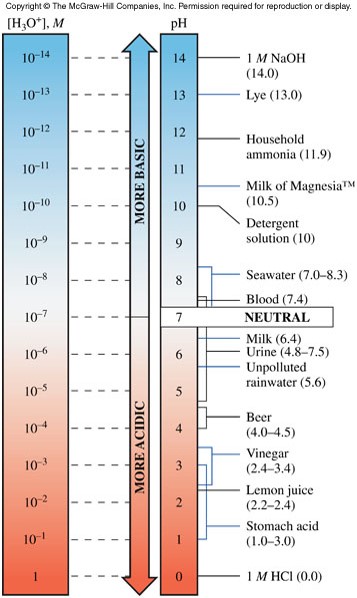
The pH Scale
- The pH of a solution is the negative logarithm (base 10) of the \(\chem{H_3O^+}\) concentration: \[ pH=-\log \left[ \chem{H_3O^+} \right] \]
- It is convenient to express the acidity of aqueous solutions on a pH scale (shown at right).
Calculating \(pOH\)
- \(pOH\) is defined as the negative logarithm (base 10) of hydroxide ion concentration, \(\left[ \chem{OH^-} \right]\): \[ pOH=-\log \left[ \chem{OH^-} \right] \] The relationship between \(pH\) and \(pOH\) is: \[ pH+pOH=14 \]
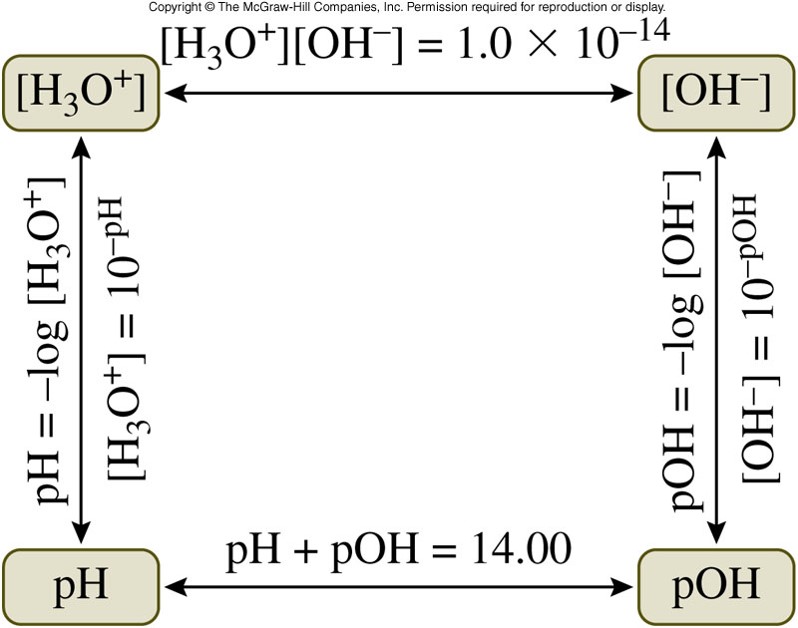
Calculating Concentrations from \(pH\) and \(pOH\)
- The equation to find \(pH\) is: \[ pH = -\log \left[ \chem{H_3O^+} \right] \]
- To find the \(\chem{H_3O^+}\) ion concentration, we need to take the inverse log of the negative \(pH\): \[ \left[ \chem{H_3O^+} \right] = 10^{-pH} \]
- The equation to find \(pOH\) is: \[ pOH = -\log \left[ \chem{OH^-} \right] \]
- To find the \(\chem{OH^-}\) ion concentration: \[ \left[ \chem{OH^-} \right] = 10^{-pOH} \]
Calculate Concentrations from pH and pOH Graphically
Measuring pH
- pH meters and \(pH\) indicators are often used to determine the \(pH\) of a solution.


Buffered Solutions
- A buffer (also known as a buffer system) is a combination of a weak acid and its conjugate base (or a weak base and its conjugate acid) in about equal concentrations.
- The main buffer system in the blood is made of \(\chem{H_2CO_3}\)/\(\chem{HCO_3^-}\):
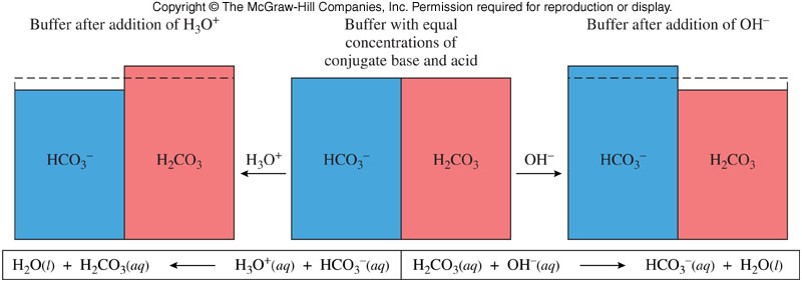
/