\( \newcommand{\xrightleftharpoons}[2]{\overset{#1}{\underset{#2}{\rightleftharpoons}}} \) \( \newcommand{\conc}[1]{\left[\mathrm{#1}\right]} \) \( \newcommand{\chem}[1]{\mathrm{#1}} \) \( \definecolor{green}{RGB}{0,128,0} \) \( \definecolor{blue}{RGB}{0,0,255} \)

Chapter 1

Matter and Energy

Shaun Williams, PhD

Matter and its Classification

Chemical Classifications of Matter

A flowchart showing that matter, anything that occupies space and has mass, can be broken down into pure substances and mixtures.

Pure Substances

Practice - Represntations of Matter

Identify the nonmetals in the following figure. Explain the characteristics you considered in making your decision.

A image showing various types of matter in their natural state.

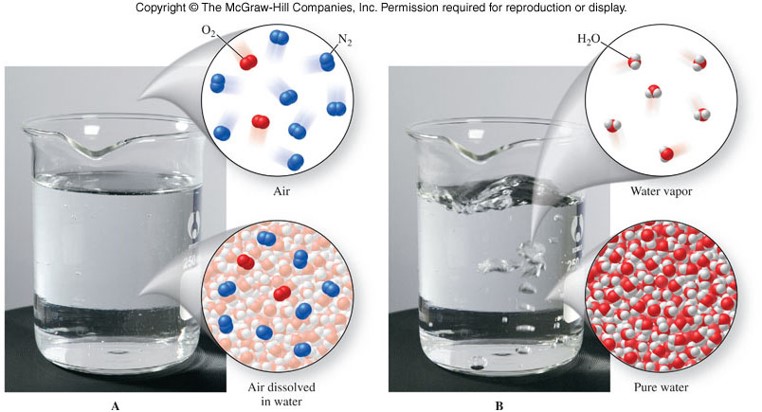
Mixtures

A flowchart showing that matter can be broken down into homogeneous (uniform in composition) and heterogeneous (not uniform in composition).

Classification of Matter

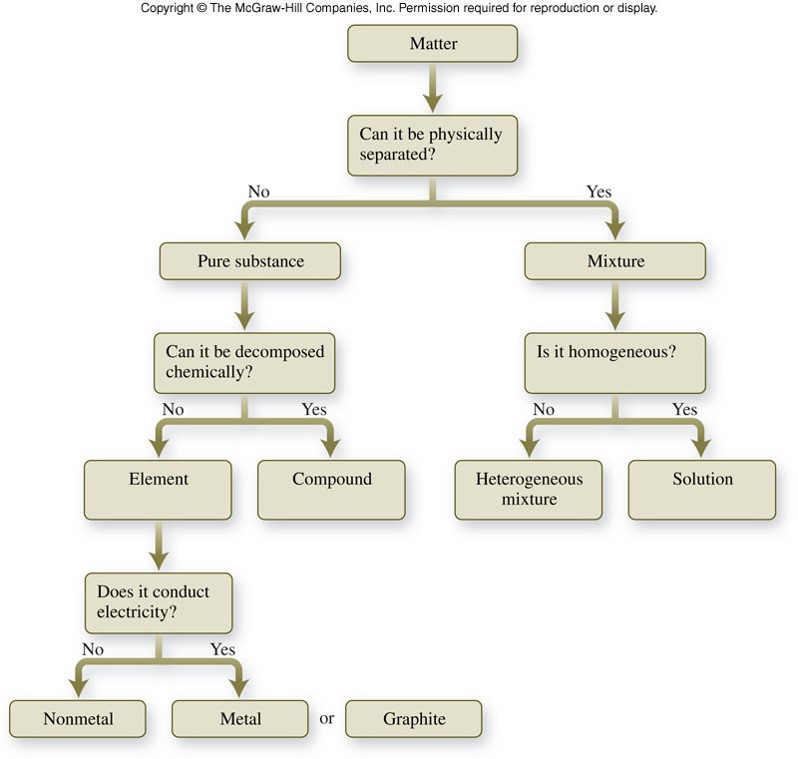
A full flowchart showing how matter is classified based on everything that we have just gone over.

Representations of Matter

  • Matter is composed of atoms.
    • An atom is the smallest unit of an element that retains the chemical properties of that element.
A picture of water in a fountain and a graphic show a collection of water molecules.

Representations of Matter 2

  • Atoms can combine together to form molecules.
    • Molecules are composed of two or more atoms bound together in a discrete arrangement.
    • The atoms bound together in a molecule can be from the same element or from different elements.
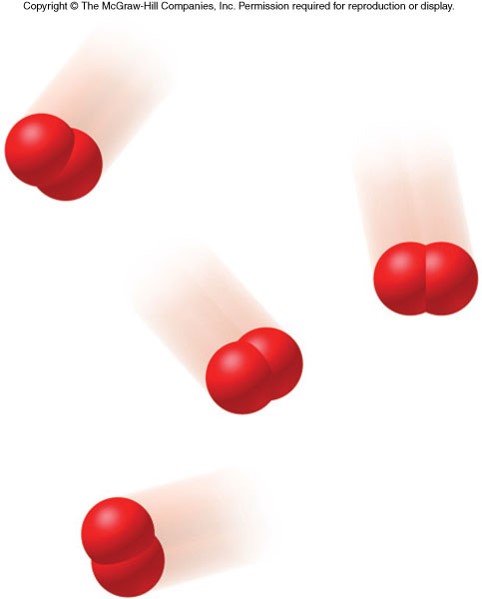
A graphic of four oxygen molecules.

States of Matter

  • Discuss the following questions with someone near you.
    • How does a solid differ from a liquid?
    • How does a gas differ from a liquid?
    • How does a solid differ from a gas?
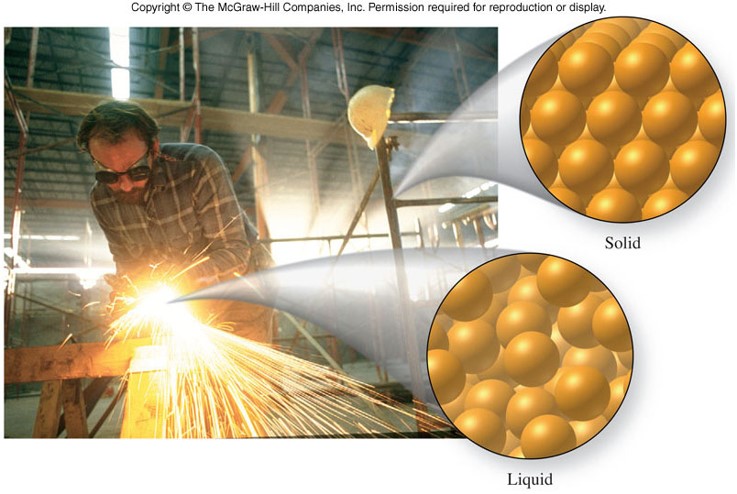
A photo of a man welding metal and a graphic showing the atoms of solid and liquid metal.

States of Matter

Solid Liquid Gas
Fixed shape Shape of continaer (may or may not fill it) Shape of container (fills it)
Its own volume Its own volume Volume of container
No volume change under pressure Slight volume change under pressure Large volume change under pressure
Particles are fixed in place in a regular array Particles are randomly arranged and free to move about until they bump into one another Particles are widely separated and move independently of one another

States of Matter - Solid and Gas

Dry ice, frozen CO2, subliming into a gaseous carbon dioxide.

States of Matter - Gas under Pressure

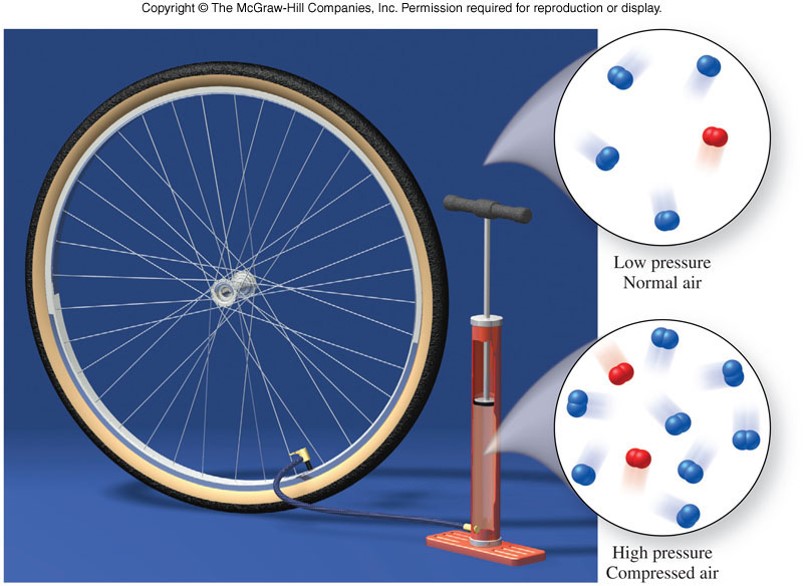
A bicycle pump connected to a bicycle tire with graphics showing that the molecules in normal air are farther apart than the air molecules in the compressed tire.

States of Matter - Liquid and Gas

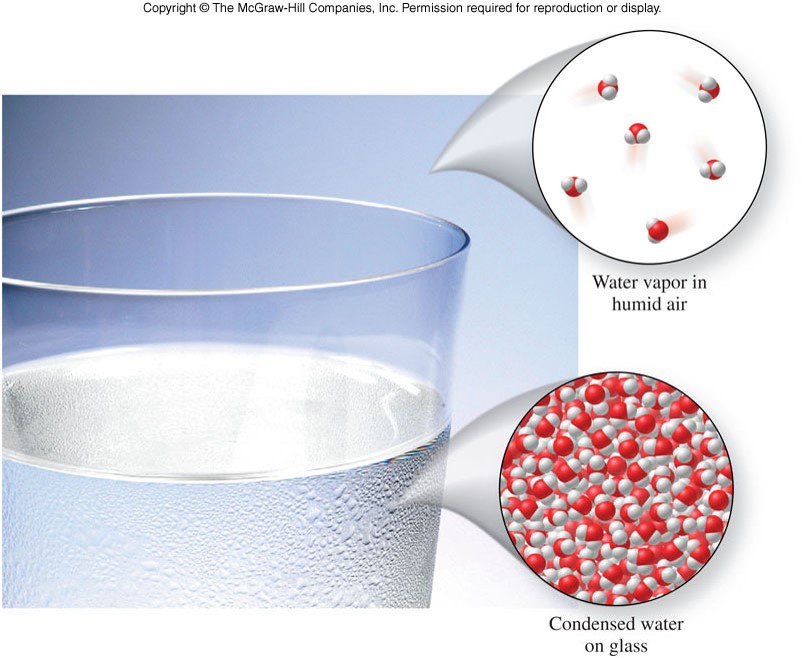
Water condensing from gaseous water into liquid water. The molecules of liquid water and on top of each other while in the gas phases, they are very far apart.

Symbols Used in Chemistry

Symbols Used in Chemistry - Examples

Name Symbol
helium He
fluorine F
silver Ag
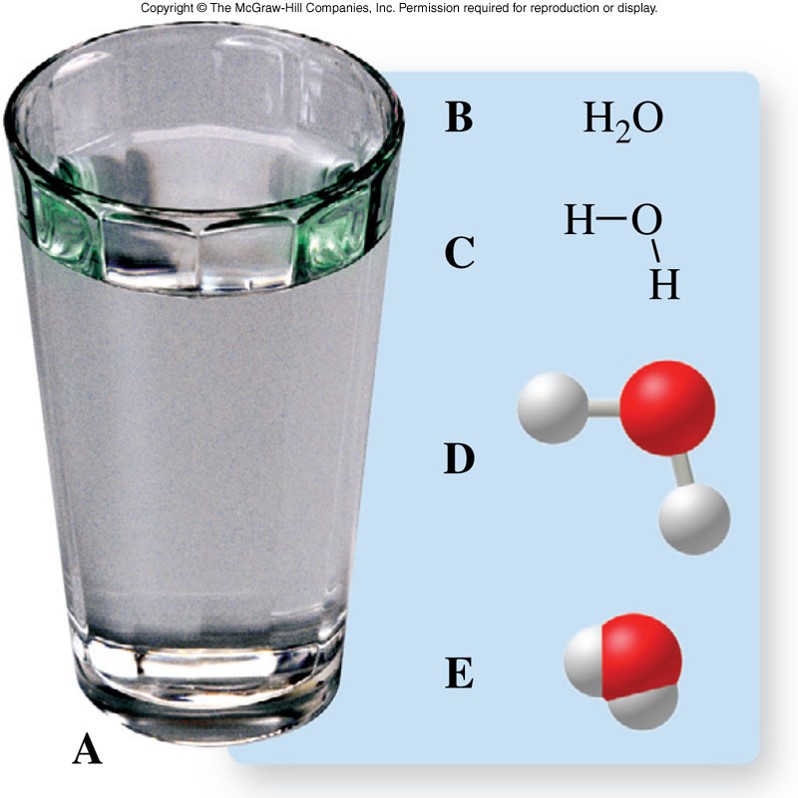
water \(\chem{H_2O}\)
carbon dioxide \(\chem{CO_2}\)
methane (natural gas) \(\chem{CH_4}\)

Symbols Used in Chemistry - Examples of Water

Water in a cut. Various ways of symbolizing the water molecules.

Symbols Used in Chemistry - Phases

  • Symbols for physical states
    • are found in parenthesis by the elemental symbol or chemical formula
    • designate the physical state [ex. solid, liquid, gas, aqueous]
    • See table to the right
Name Symbol
solid (s)
liquid (l)
gas (g)
aqueous (dissolved in water) (aq)

Physical and Chemical Changes and Properties of Matter

Physical Properties of Matter

Mass

  • Mass:
    • measures the quantity of matter
    • is essentially the same physical quantity as weight, with the exception that weight is bound by gravity, mass is not
    • common units are grams (g)
Two objects on a two pan balance.

Volume

  • Volume:
    • amount of space a substance occupies
    • can be calculated by measuring the sides of a cube or rectangular side, then multiplying them \[ \chem{Volume = l \times w \times h} \]
    • common units are centimeters cubed (\(\chem{cm^3}\)) or milliliters (\(\chem{mL}\))
Three chemistry containers containing liquids and three common containers of liquids.

Density

  • Density:
    • the ratio of the mass to its volume \[ \chem{density = \frac{mass}{volume}} \]
    • units are \( \bfrac{g}{mL} \) (solids and liquids) or \( \bfrac{g}{L} \) (gases)
    • See Table 1.4 for a listing of densities for common substances
Different colored liquids of different colors and different densities. The liquids stack and seperate by density.

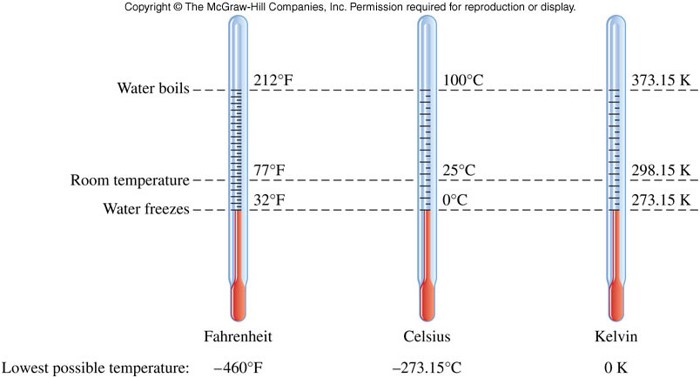
Temperature

  • Temperature:
    • a measure of how hot or cold something is relative to some standard
    • is measured with a thermometer
    • at which a phase change occurs is independent of sample size
    • units are degrees Celsius (\( \chem{{}^\circ C} \)) and degrees Kelvin (\(\chem{K}\)) \[ \chem{T_K = T_{{}^\circ C} + 273.15} \] \[ \chem{T_{{}^\circ F} = 1.8 \left( T_{{}^\circ C} \right) + 32} \]
Three thermometers showing the differences between the Fahrenheit, Celsius, and Kelvin temperature scales.

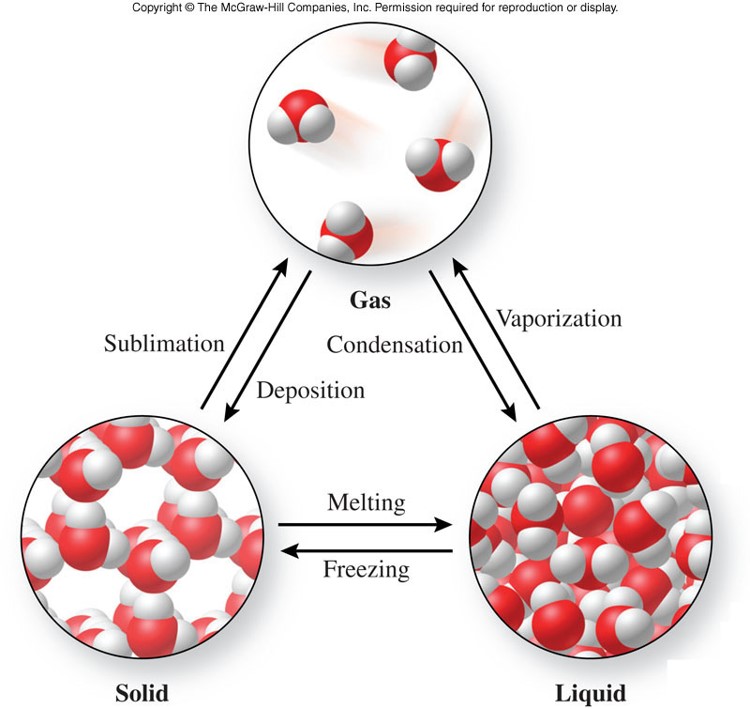
Physical Changes

  • A physical change
    • is a process that changes the physical properties of a substance without changing its chemical composition
    • evidence of a physical change includes:
      • a change of state
        • Example: water changes from a solid to a gas
      • an expected change in color
A graphic showing all the phase changes between solid, liquid, and gas states.

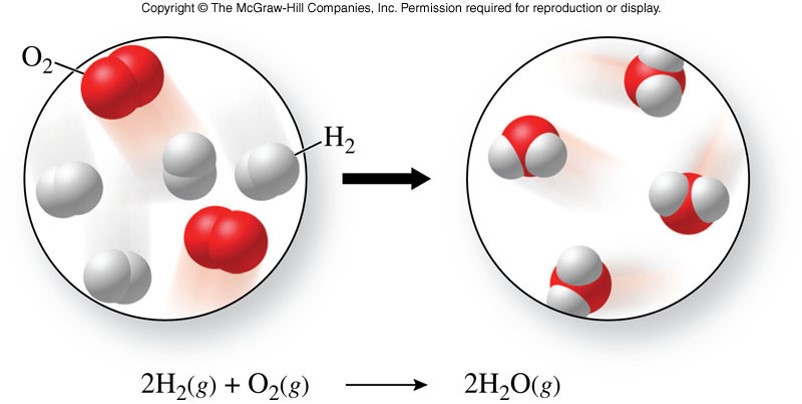
Chemical Changes

  • A chemical change
    • is a process in which one or more substances are converted into one or more new substances
    • also called a chemical reaction
    • evidence of a chemical change includes:
      • bubbling
      • a permanent color change
      • a sudden change in temperature
A graphic showing gas dissolved into water while boiling water has gaseous water inside the liquid water.

Chemical Properties

  • Defined by what it is composed of and what chemical changes it can undergo
A graphic showing hydrogen and oxygen molecules becoming water molecules.

Energy and Energy Change

What is Energy?

Example: Energy Change

A ball of flame from the burning of hydrogen gas.

Energy Units

Example: Energy Units

The nutrition label sample from food.

The Scientific Method

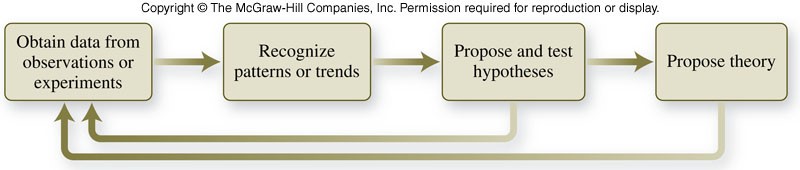
What is the scientific method?

Some parts of the scientific method

Flowchart of the Scientific Method

The steps of the scientific method laid out in order showing how they are used.

Math

Scientific Notation

Scientific Notation - Examples

Normal Notation Scientific Notation
3245. \( 3.245 \times 10^3 \)
0.000003245 \( 3.245 \times 10^{-6} \)
3,245,000,000 \( 3.245 \times 10^9 \)
0.0050607 \( 5.0607 \times 10^{-3} \)
88. \( 8.8 \times 10^1 \)
2.45 \( 2.45 \times 10^0 \)

Poor Precision, Poor Accuracy

Horse shoes missing the pole and scattered everywhere showing poor accuracy and poor precision.

Good Precision, Poor Accuracy

Horse shoes missing the pole but clustered together showing poor accuracy but good precision.

Good Precision, Good Accuracy

Horse shoes at the pole and clusted together showing good accuracy and good precision.

Significant Figures - Step 1

Here is a simpler method for determining the number of significant figures in a given measurement.

  1. Underline the left-most nonzero digit.
    • 273.1023
    • 0.1023
    • 10.025
    • 1020

Significant Figures - Step 2

  1. Look for a written decimal point in the number.
    1. If the number contains a decimal point, underline the right-most digit.
      • 273.1023
      • 0.1023
      • 10.025
    2. If the number does not contain a decimal point, underline the right-most nonzero digit.
      • 1020

Significant Figures - Step 3

  1. Count the number between the underlined numbers (including those underlined)
    • 273.1023 ← 7 sig. figs.
    • 0.1023 ← 4 sig. figs.
    • 10.025 ← 5 sig. figs.
    • 1020 ← 3 sig. figs.

Special Types of Numbers

Significant Figures in Mathematical Operations

  1. For multiplication or division, the number of significant figures in the result is the same as the number in the least precise measurement used in the calculation. $$ 1.342 \times \underline{5.5} = 7.381 \xrightarrow{\chem{round}} \underline{7.4} $$
  2. For addition or subtraction, the result has the same number of decimal places as the least precise measurement used in the calculation. $$ 23.445 + 7.8\underline{3} = 31.275 \xrightarrow{\chem{round}} 31.2\underline{8} $$

Units

  • Measurement
    • is the determination of the size of a particular quantity
    • Measurements are defined by both a quantity (number) and unit.
    • Most scientists use SI (from the French for Système Internationale) units (see top chart or chart on pg. 39).
Unit Symbol Quantity
meter m length
kilogram kg mass
second s time
ampere A electric current
Kelvin K temperature
mole mol amount of substance

Units - Prefixes

  • Scientists also use the metric system to define base units of measure, with the understanding that a special prefix denotes fractions or multiples of that base (see chart on right).
Prefix Factor Symbol
giga \( 10^9 \) G
mega \( 10^6 \) M
kilo \( 10^3 \) k
deci \( 10^{-1} \) d
centi \( 10^{-2} \) c
milli \( 10^{-3} \) m
micro \( 10^{-6} \) μ
nano \( 10^{-9} \) n

Unit Analysis

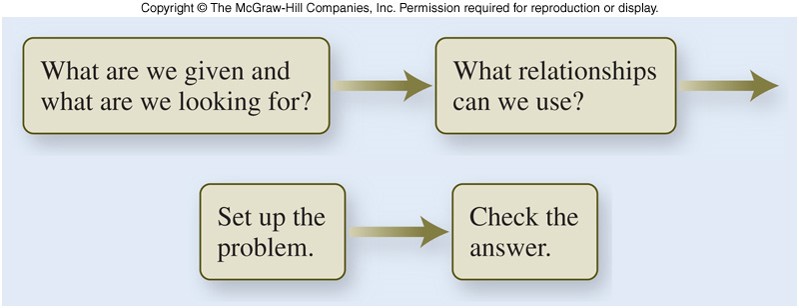
A possible approach to problem solving involves 4 steps:

  1. Decide what the problem is asking for.
  2. Decide what relationships exist between the information given in the problem and the desired quantity.
  3. Set up the problem logically, using the relationships decided upon in step 2.
  4. Check the answer to make sure it makes sense, both in magnitude and units.

Unit Analysis - Flowchart

A flowchart showing the steps we use to analyze conversions from one unit to another.

← →

/