Chapter 9
Gases
Shaun Williams, PhD
Why Study Gases
- An understanding of real world phenomena.
- An understanding of how science "works."
A Gas
- Uniformly fills any container.
- Easily compressed.
- Mixes completely with any other gas.
- Exerts pressure on its surroundings.
Pressure
$$ \text{Pressure}=\frac{\text{force}}{\text{area}} $$
- \( \text{SI units} = \bfrac{\text{Newton}}{\text{meter}^2} = 1\, \text{Pascal (Pa)} \)
- \( 1\,\text{standard atmosphere} = 101,325\,\chem{Pa} \)
- \( 1\,\text{standard atmosphere} = 1\,\chem{atm} = 760\,\text{mm Hg} = 760\,\text{torr} \)
Barometer
- Device used to measure atmospheric pressure.
- Mercury flows out of the tube until the pressure of the column of mercury standing on the surface of the mercury in the dish is equal to the pressure of the air on the rest of the surface of the mercury in the dish.

Manometer
- Device used for measuring the pressure of a gas in a container.

Collapsing Can

Pressure Conversions: An Example
The pressure of a gas is measured as 2.5 atm. Represent this pressure in both torr and pascals.
Pressure Conversions: An Example - Answer
The pressure of a gas is measured as 2.5 atm. Represent this pressure in both torr and pascals.
$$ \left( 2.5\,\chem{atm} \right) \times \left( \frac{760\,\chem{torr}}{1\,\chem{atm}} \right) = 1.9\times 10^3\,\chem{torr} $$ $$ \left( 2.5\,\chem{atm} \right) \times \left( \frac{101325\,\chem{Pa}}{1\,\chem{atm}} \right) = 2.5\times 10^5\,\chem{Pa} $$The Gas Laws of Boyle, Charles, and Avogadro
Liquid Nitrogen and a Balloon

- What happened to the gas in the balloon?
- A decrease in temperature was followed by a decrease in the pressure and volume of the gas in the balloon.
- This is an observation (a fact).
- It does NOT explain "why," but it does tell us "what happened."
Gas Laws
- Gas laws can be deduced from observations like these.
- Mathematical relationships among the properties of a gas (Pressure, Volume, Temperature and Moles) can be discovered.
Boyle's Law
- Pressure and volume are inversely related (constant \(T\), temperature, and \(n\), # of moles of gas).
- \( PV = k \) (\(k\) is a constant for a given sample of air at a specific temperature) $$ P_1 \times V_1 = P_2 \times V_2 $$
Exercise 1
A sample of helium gas occupies 12.4 L at 23°C and 0.956 atm. What volume will it occupy at 1.20 atm assuming that the temperature stays constant?
Exercise 1 - Answer
A sample of helium gas occupies 12.4 L at 23°C and 0.956 atm. What volume will it occupy at 1.20 atm assuming that the temperature stays constant?
$$ 9.88\,\chem{L} $$Charles' Law
- Volume and Temperature (in Kelvin) are directly related (constant \(P\) and \(n\)).
- \(V=bT\) (\(b\) is a proportionality constant)
- \(\chem{K} = {}^\circ\chem{C} + 273.15\)
- \(0\,\chem{K}\) is called absolute zero. $$ \frac{V_1}{T_1} = \frac{V_2}{T_2} $$
Exercise 2
Suppose a balloon containing 1.30 L of air at 24.7°C is placed into a beaker containing liquid nitrogen at –78.5°C. What will the volume of the sample of air become (at constant pressure)?
Exercise 2 - Answer
Suppose a balloon containing 1.30 L of air at 24.7°C is placed into a beaker containing liquid nitrogen at –78.5°C. What will the volume of the sample of air become (at constant pressure)?
$$ 0.849\,\chem{L} $$Avogadro's Law
- Volume and number of moles are directly related (constant \(T\) and \(P\)).
- \(V = an\) (\(a\) is a proportionality constant) $$ \frac{n_1}{V_1}=\frac{n_2}{V_2} $$
Exercise 3
If 2.45 mol of argon gas occupies a volume of 89.0 L, what volume will 2.10 mol of argon occupy under the same conditions of temperature and pressure?
Exercise 3 - Answer
If 2.45 mol of argon gas occupies a volume of 89.0 L, what volume will 2.10 mol of argon occupy under the same conditions of temperature and pressure?
$$ 76.3\,\chem{L} $$The Ideal Gas Law
Bringing the Law Together
- We can bring all of these laws together into one comprehensive law:
- \(V = bT\) (constant \(P\) and \(n\))
- \(V = an\) (constant \(T\) and \(P\))
- \(V = \frac{k}{P} \) (constant \(T\) and \(n\))
$$ PV=nRT $$ where \(R=0.08206\,\bfrac{\chem{L\cdot atm}}{\chem{mol\cdot K}}\), the universal gas constant.
Exercise 4
An automobile tire at 23°C with an internal volume of 25.0 L is filled with air to a total pressure of 3.18 atm. Determine the number of moles of air in the tire.
Exercise 4 - Answer
An automobile tire at 23°C with an internal volume of 25.0 L is filled with air to a total pressure of 3.18 atm. Determine the number of moles of air in the tire.
$$ 3.27\,\chem{mol} $$Exercise 5
What is the pressure in a 304.0 L tank that contains 5.670 kg of helium at 25°C?
Exercise 5 - Answer
What is the pressure in a 304.0 L tank that contains 5.670 kg of helium at 25°C?
$$ 114\,\chem{atm} $$Exercise 6
At what temperature (in °C) does 121 mL of \(\chem{CO_2}\) at 27°C and 1.05 atm occupy a volume of 293 mL at a pressure of 1.40 atm?
Exercise 6 - Answer
At what temperature (in °C) does 121 mL of \(\chem{CO_2}\) at 27°C and 1.05 atm occupy a volume of 293 mL at a pressure of 1.40 atm?
$$ 696^\circ\,\chem{C} $$Gas Stoichiometry
Molar Volume of an Ideal Gas
- For 1 mole of an ideal gas at 0°C and 1 atm, the volume of the gas is 22.42 L. $$ V=\frac{nRT}{P}=\frac{(1.000\,\chem{mol})\left(0.08206\,\frac{\chem{L\cdot atm}}{\chem{K\cdot mol}}\right)(273.2\,\chem{K})}{1.000\,\chem{atm}}=22.42\,\chem{L} $$
- STP = standard temperature and pressure
- \(0^\circ\chem{C}\) and \(1\,\chem{atm}\)
- Therefore, the molar volume is \(22.42\,\chem{L}\) at STP.
Exercise 7
A sample of oxygen gas has a volume of \(2.50\,\chem{L}\) at STP. How many grams of \(\chem{O_2}\) are present?
Exercise 7 - Answer
A sample of oxygen gas has a volume of \(2.50\,\chem{L}\) at STP. How many grams of \(\chem{O_2}\) are present?
$$ 3.57\,\chem{g} $$Molar Mass of a Gas
$$ \text{Molar Mass}=\frac{dRT}{P} = \frac{\left( \frac{\chem{g}}{\cancel{\chem{L}}} \right)\left( \frac{\chem{\cancel{L}\cdot \cancel{atm}}}{\chem{mol\cdot \cancel{K}}} \right)\left( \chem{\cancel{K}} \right)}{\left( \chem{\cancel{atm}} \right)} $$
- \(d\) = density of gas
- \(T\) = temperature in Kelvin
- \(P\) = pressure of gas
- \(R\) = universal gas constant
Exercise 8
What is the density of \(\chem{F_2}\) at STP (in \(\bfrac{\chem{g}}{\chem{L}}\))?
Exercise 8 - Answer
What is the density of \(\chem{F_2}\) at STP (in \(\bfrac{\chem{g}}{\chem{L}}\))?
$$ 1.70\,\bfrac{\chem{g}}{\chem{L}} $$Dalton's Law of Partial Pressures
- For a mixture of gases in a container, $$ P_\chem{Total} = P_1+P_2+P_3+\cdots $$
- The total pressure exerted is the sum of the pressures that each gas would exert if it were alone.

Exercise 9
Consider the following apparatus containing helium in both sides at 45°C. Initially the valve is closed. After the valve is opened, what is the pressure of the helium gas?
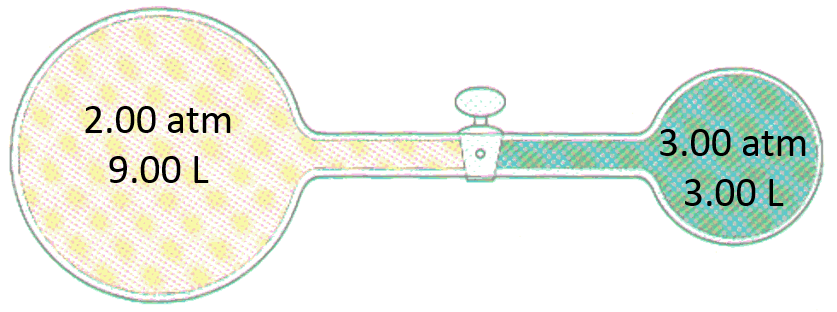
Exercise 9 - Answer
Consider the following apparatus containing helium in both sides at 45°C. Initially the valve is closed. After the valve is opened, what is the pressure of the helium gas?

The Kinetic Molecular Theory of Gases
- So far we have considered "what happens," but not "why."
- In science, "what" always comes before "why."
Postulates of the Kinetic Molecular Theory
- The particles are so small compared with the distances between them that the volume of the individual particles can be assumed to be negligible (zero).

- The particles are in constant motion. The collisions of the particles with the walls of the container are the cause of the pressure exerted by the gas.
- The particles are assumed to exert no forces on each other; they are assumed neither to attract nor to repel each other.
- The average kinetic energy of a collection of gas particles is assumed to be directly proportional to the Kelvin temperature of the gas.
Root Mean Square Velocity
$$ u_{rms} = \sqrt{\frac{3RT}{M}} $$
- \(R = 8.3145\,\bfrac{\chem{J}}{\chem{K\cdot mol}}\) (\(\chem{J}= \chem{joule} = \bfrac{\chem{kg\cdot m^2}}{\chem{s^2}}\))
- \(T\) = temperature of gas (in \(\chem{K}\))
- \(M\) = mass of a mole of gas in \(\chem{kg}\)
- Final units are in \(\bfrac{\chem{m}}{\chem{s}}\).
Effusion and Diffusion
- Diffusion – the mixing of gases.
- Effusion – describes the passage of a gas through a tiny orifice into an evacuated chamber.
- Rate of effusion measures the speed at which the gas is transferred into the chamber.
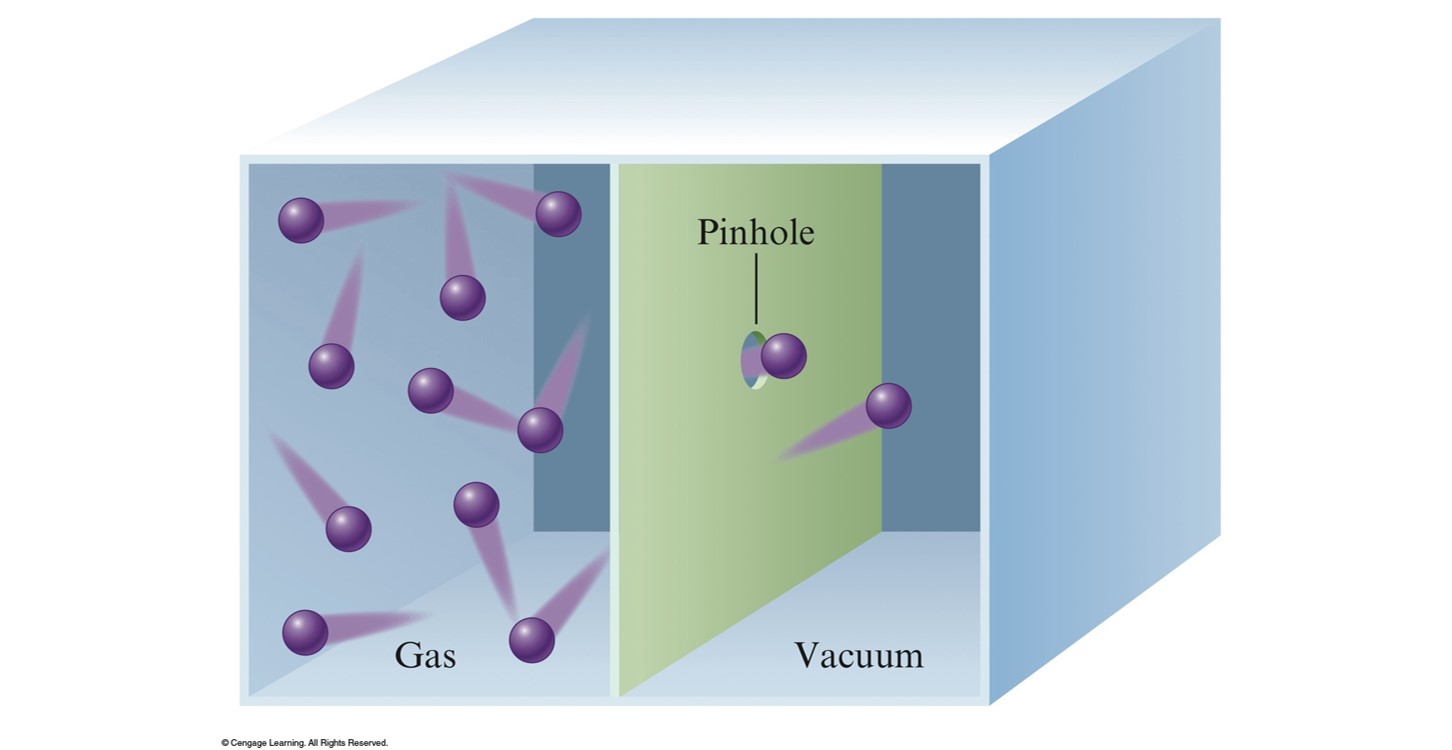
Graham's Law of Effusion
$$ \frac{\text{Rate of effusion for gas 1}}{\text{Rate of effusion for gas 2}} = \frac{\sqrt{M_2}}{\sqrt{M_1}} $$
- \(M_1\) and \(M_2\) represent the molar masses of the gases.
Real Gases
- An ideal gas is a hypothetical concept. No gas exactly follows the ideal gas law.
- We must correct for non-ideal gas behavior when:
- Pressure of the gas is high.
- Temperature is low.
- Under these conditions:
- Concentration of gas particles is high.
- Attractive forces become important.
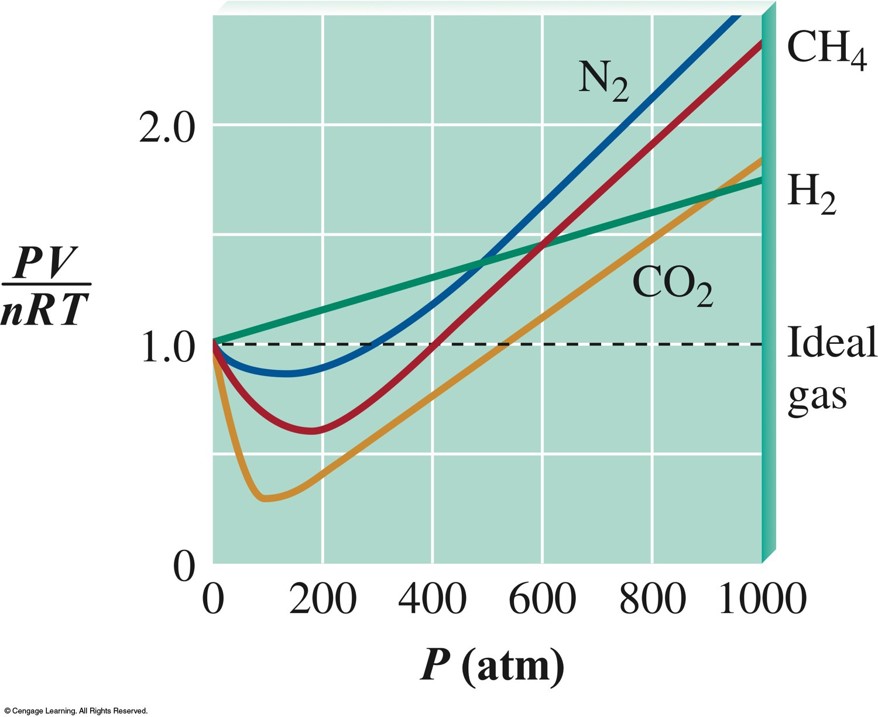
Plots of \(\bfrac{PV}{nRT}\) Versus \(P\) for Several Gases (\(200\,\chem{K}\))
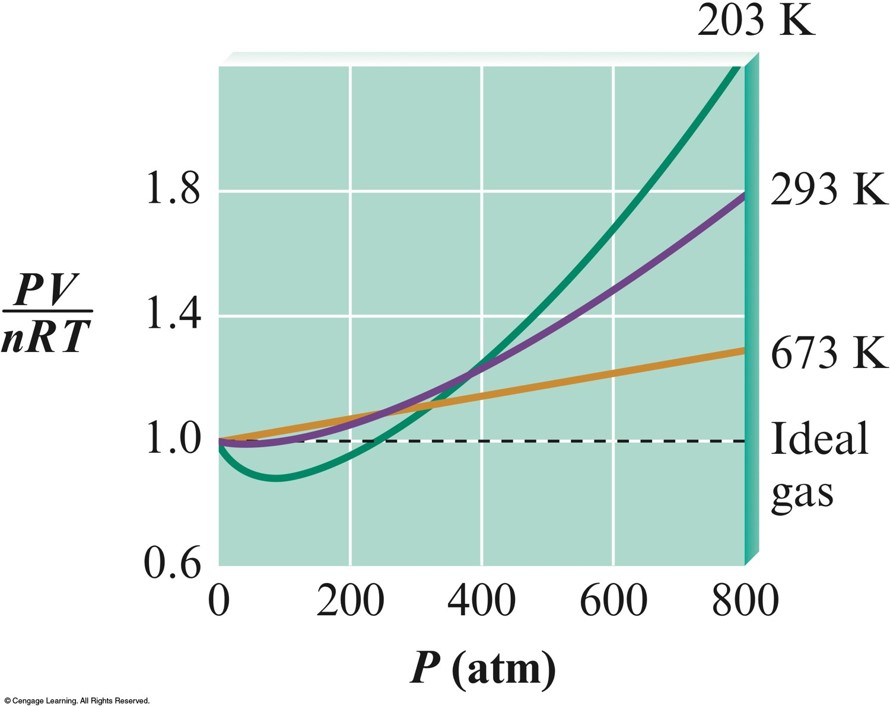
Plots of \(\bfrac{PV}{nRT}\) Versus \(P\) for Nitrogen Gas at Three Temperatures
Real Gases (van der Waals Equation)
$$ \underbrace{\left[ P_\chem{obs} + a \left(\frac{n}{V}\right)^2 \right]}_{\text{corrected pressure, }P_\chem{ideal}} \times \underbrace{\left( V-nb \right)}_{\text{corrected volume, }V_\chem{ideal}} = nRT $$
Characteristics of Several Real Gases
- For a real gas, the actual observed pressure is lower than the pressure expected for an ideal gas due to the intermolecular attractions that occur in real gases.
Values of the van der Waals Constants for Some Gases
- The value of \(a\) reflects how much of a correction must be made to adjust the observed pressure up to the expected ideal pressure.
- A low value for \(a\) reflects weak intermolecular forces among the gas molecules.
| Gas | \(a\,\left(\frac{\chem{atm\cdot L^2}}{\chem{mol^2}}\right)\) | \(b\,\left(\frac{\chem{L}}{\chem{mol}}\right)\) |
|---|---|---|
| \(\chem{He}\) | 0.0341 | 0.0237 |
| \(\chem{Ne}\) | 0.211 | 0.0171 |
| \(\chem{Ar}\) | 1.35 | 0.0322 |
| \(\chem{Kr}\) | 2.32 | 0.0398 |
| \(\chem{Xe}\) | 4.19 | 0.0511 |
| \(\chem{H_2}\) | 0.244 | 0.0266 |
| \(\chem{N_2}\) | 1.39 | 0.0391 |
| \(\chem{O_2}\) | 1.36 | 0.0318 |
| \(\chem{Cl_2}\) | 6.49 | 0.0562 |
| \(\chem{CO_2}\) | 3.59 | 0.0427 |
| \(\chem{CH_4}\) | 2.25 | 0.0428 |
| \(\chem{NH_3}\) | 4.17 | 0.0371 |
| \(\chem{H_2O}\) | 5.46 | 0.0305 |
Chemistry in the Atmosphere
Air Pollution
- Two main sources:
- Transportation
- Production of electricity
- Combustion of petroleum produces \(\chem{CO}\), \(\chem{CO_2}\), \(\chem{NO}\), and \(\chem{NO_2}\), along with unburned molecules from petroleum.
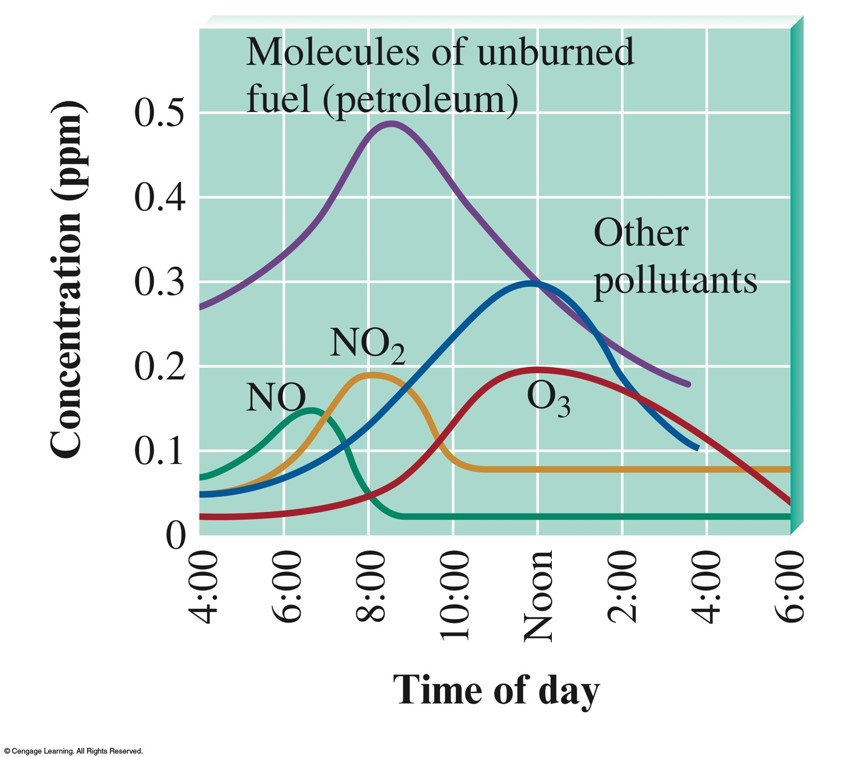
Nitrogen Oxides (Due to Cars and Trucks)
- At high temperatures, \(\chem{N_2}\) and \(\chem{O_2}\) react to form \(\chem{NO}\), which oxidizes to \(\chem{NO_2}\).
- The \(\chem{NO_2}\) breaks up into nitric oxide and free oxygen atoms.
- Oxygen atoms combine with \(\chem{O_2}\) to form ozone (\(\chem{O_3}\)).
$$ \begin{align} \chem{NO_2(g)} & \xrightarrow{\text{h$\nu$}} \chem{NO(g) + O(g)} \\ \chem{O(g) + O_2(g)} & \rightarrow \chem{O_3(g)} \end{align} $$
Concentration for Some Smog Components vs. Time of Day
Sulfur Oxides (Due to Burning Coal for Electricity
- Sulfur produces \(\chem{SO_2}\) when burned.
- \(\chem{SO_2}\) oxidizes into \(\chem{SO_3}\), which combines with water droplets in the air to form sulfuric acid.
$$\begin{align} \chem{S}\text{(in coal)}\chem{+O_2(g)} & \rightarrow \chem{SO_2(g)} \\ \chem{2SO_2(g)+O_2(g)} & \rightarrow \chem{2SO_3(g)} \\ \chem{SO_3(g)+H_2O(l)} & \rightarrow \chem{H_2SO_4(aq)} \\ \end{align}$$
- Sulfuric acid is very corrosive and produces acid rain.
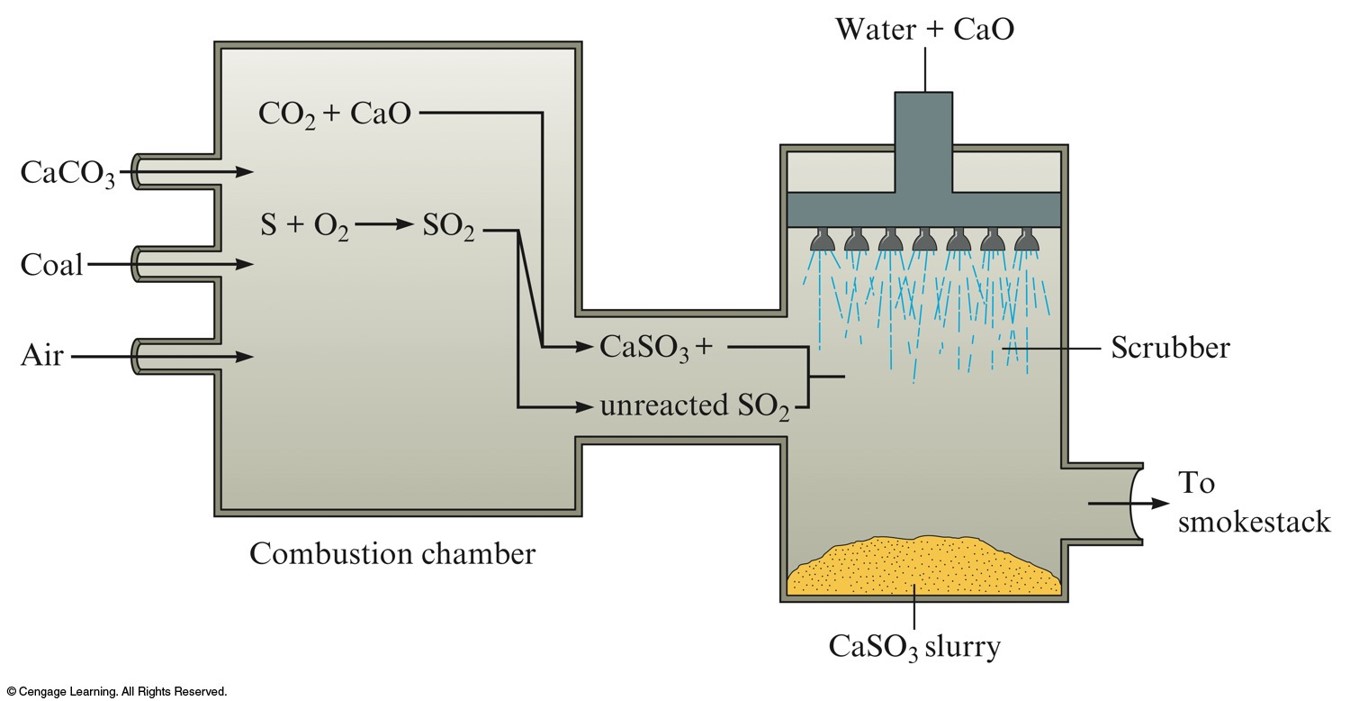
- Use of a scrubber removes \(\chem{SO_2}\) from the exhaust gas when burning coal.
A Schematic Diagram of a Scrubber
/