Chapter 7

Chemical Bonding and Molecular Geometry

Shaun Williams, PhD

Questions to Consider

• What is meant by the term "chemical bond"?
• Why do atoms bond with each other to form compounds?
• How do atoms bond with each other to form compounds?

Types of Chemical Bonds

A Chemical Bond

• No simple, and yet complete, way to define this.
• Forces that hold groups of atoms together and make them function as a unit.
• A bond will form if the energy of the aggregate is lower than that of the separated atoms.

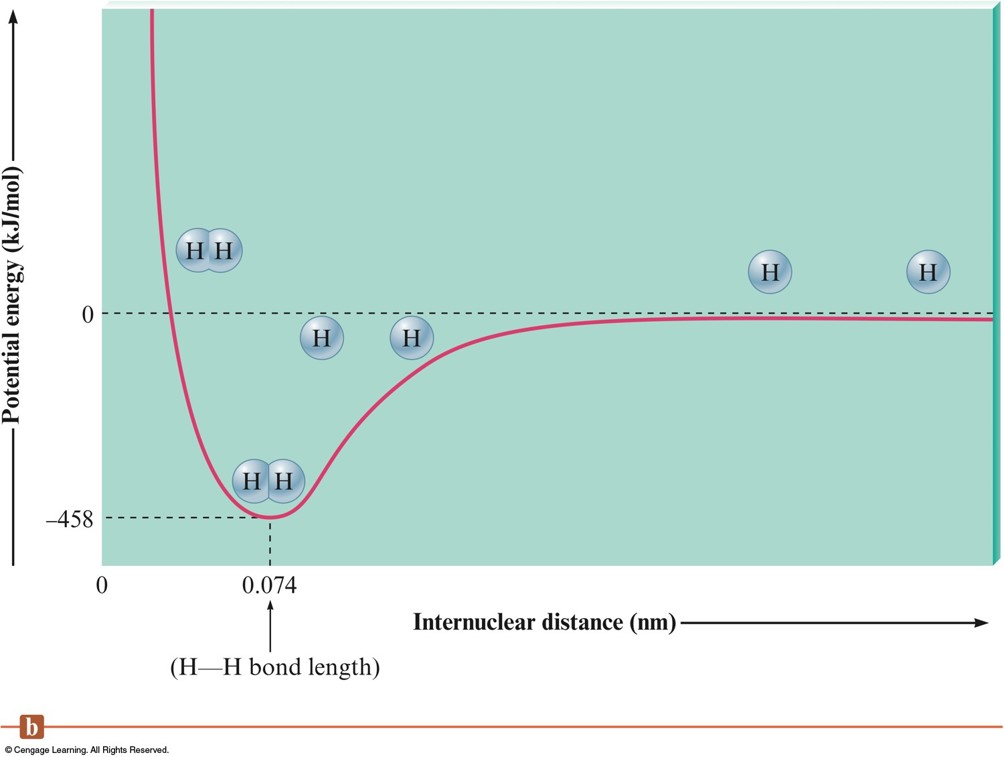
The Interaction of Two Hydrogen Atoms

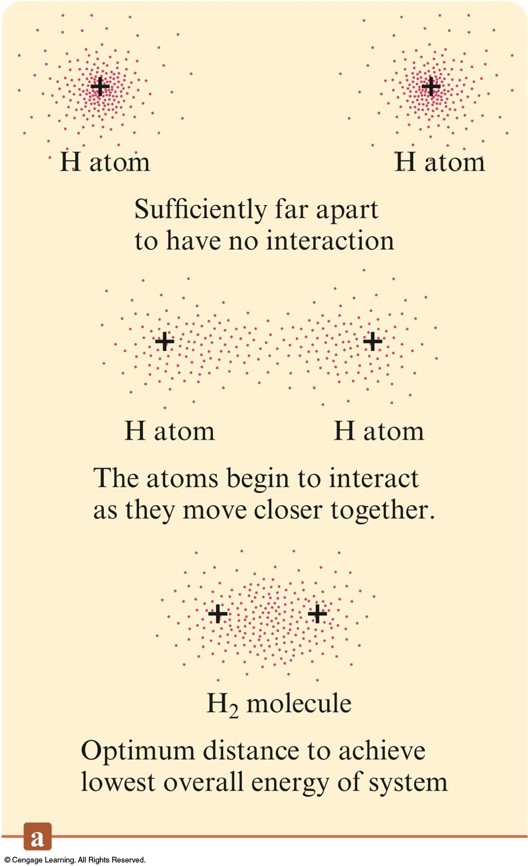
The Interaction of Two Hydrogen Atoms - Plot

Key Ideas in Bonding

• Ionic Bonding - electrons are transferred
• Covalent Bonding - electrons are shared equally by nuclei
• What about intermediate cases?

Polar Covalent Bond

• Unequal sharing of electrons between atoms in a molecule.
• Results in a charge separation in the bond (partial positive and partial negative charge).

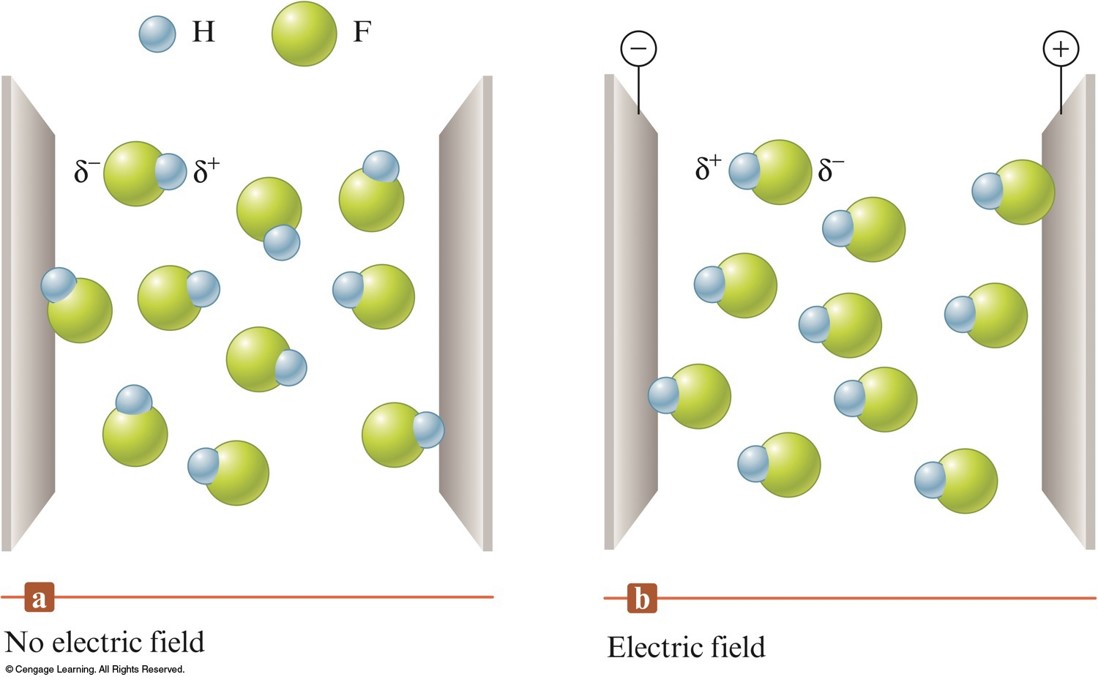
The Effect of an Electric Field on Hydrogen Fluoride Molecules

\(\delta^-\) or \(\delta^+\) indicates a positive or negative fractional charge.

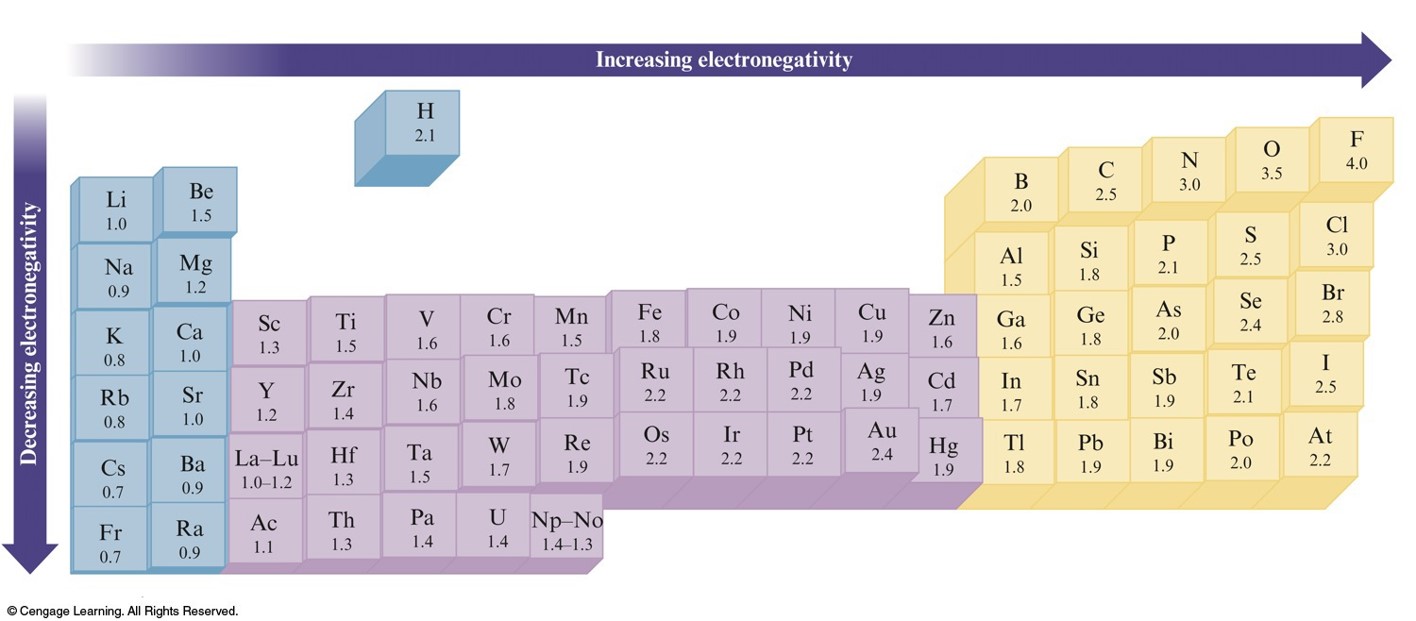
Electronegativity

• The ability of an atom in a molecule to attract shared electrons to itself.
• For a molecule HX, the relative electronegativities of the H and X atoms are determined by comparing the measured H–X bond energy with the "expected" H–X bond energy.
• On the periodic table, electronegativity generally increases across a period and decreases down a group.
• The range of electronegativity values is from 4.0 for fluorine (the most electronegative) to 0.7 for cesium (the least electronegative).

The Pauling Electronegativity Values

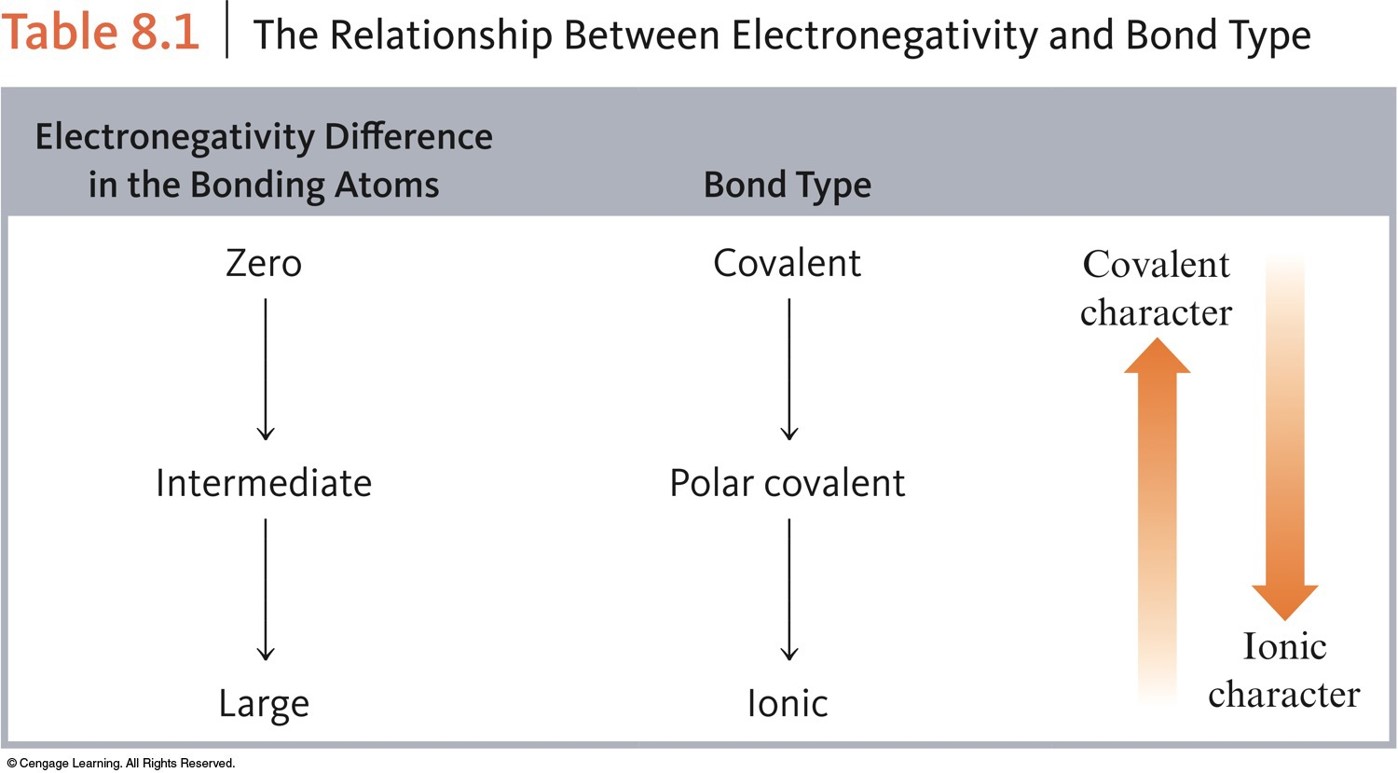
The Relationship Between Electronegativity and Bond Type

Exercise 1

Arrange the following bonds from most to least polar:

1. N-F, O-F, C-F
2. C-F, N-O, Si-F
3. Cl-Cl, B-Cl, S-Cl

Exercise 1 - Answer

Arrange the following bonds from most to least polar:

1. N-F, O-F, C-F → C-F, N-F, O-F
2. C-F, N-O, Si-F → Si-F, C-F, N-O
3. Cl-Cl, B-Cl, S-Cl → B-Cl, S-Cl, Cl-Cl

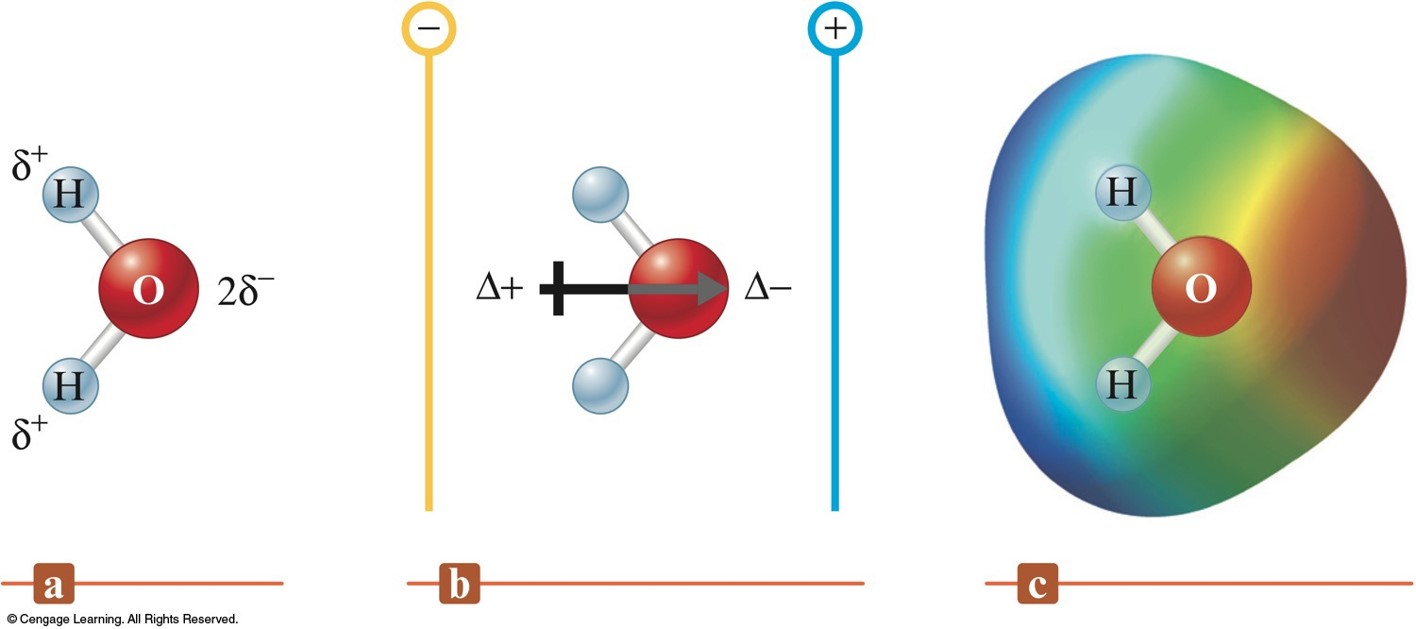
Bond Polarity and Dipole Moments

Dipole Moment

• Property of a molecule whose charge distribution can be represented by a center of positive charge and a center of negative charge.
• Use an arrow to represent a dipole moment.
  • Point to the negative charge center with the tail of the arrow indicating the positive center of charge.

Dipole Moment in Water

Dipole Moment in Carbon Dioxide - No Net Dipole Moment (Dipoles Cancel)

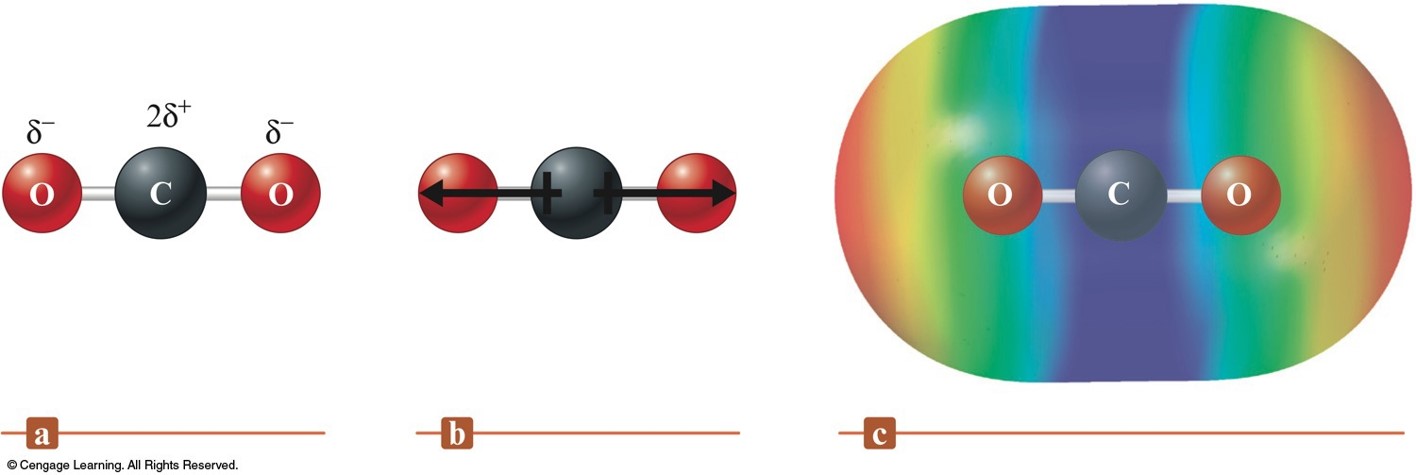
Ions: Electron Configurations and Sizes

Stable Compounds

• Atoms in stable compounds usually have a noble gas electron configuration.

Electron Configurations in Stable Compounds

• When two nonmetals react to form a covalent bond, they share electrons in a way that completes the valence electron configurations of both atoms.
• When a nonmetal and a representative-group metal react to form a binary ionic compound, the ions form so that the valence electron configuration of the nonmetal achieves the electron configuration of the next noble gas atom. The valence orbitals of the metal are emptied.

Isoelectronic Series

• A series of ions/atoms containing the same number of electrons. $$ \chem{O^{2-},\;F^-,\;Ne,\;Na^+,\;Mg^{2+},\;and\; Al^{3+}} $$

Periodic Table Allows Us to Predict Many Properties

• Trends for:
  • Atomic size, ion radius, ionization energy, electronegativity
• Electron configurations
• Formula prediction for ionic compounds
• Covalent bond polarity ranking

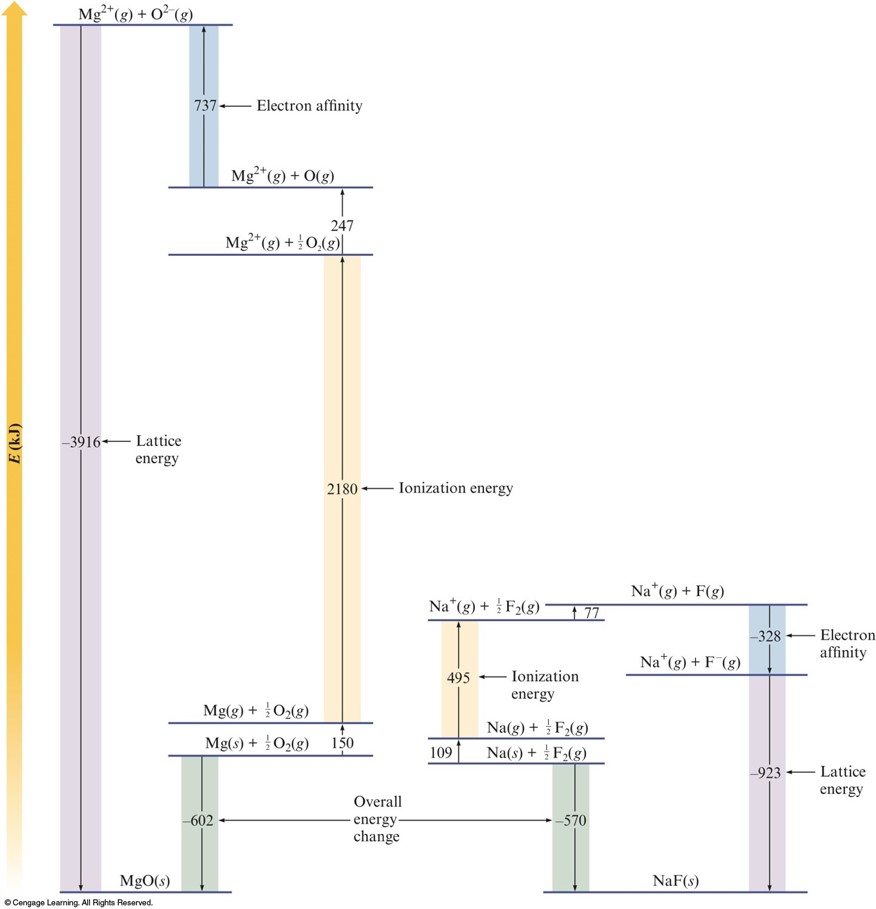
Energy Effects in Binary Ionic Compounds

• What are the factors that influence the stability and the structures of solid binary ionic compounds?
• How strongly the ions attract each other in the solid state is indicated by the lattice energy.

Lattice Energy

• The change in energy that takes place when separated gaseous ions are packed together to form an ionic solid. $$ \text{Lattice energy}=k\left(\frac{Q_1Q_2}{r}\right) $$
  • \(k\) = proportionality constant
  • \(Q_1\) and \(Q_2\) = charges on the ions
  • \(r\) = shortest distance between the centers of the cations and anions

Formation of an Ionic Solid

• Sublimation of the solid metal.
  • \( \chem{M(s) \rightarrow M(g)}\;\; \text{[endothermic]} \)
• Ionization of the metal atoms.
  • \( \chem{M(g) \rightarrow M^+(g) + e^-}\;\; \text{[endothermic]} \)
• Dissociation of the nonmetal.
  • \( \chem{\frac{1}{2}X_2(g) \rightarrow X(g)}\;\; \text{[endothermic]} \)
• Formation of nonmetal ions in the gas phase.
  • \( \chem{X(g) + e^- \rightarrow X^-(g)}\;\; \text{[exothermic]} \)
• Formation of the solid ionic compound.
  • \( \chem{M^+(g) + X^-(g) \rightarrow MX(s)}\;\; \text{[quite exothermic]} \)

Comparing Energy Changes

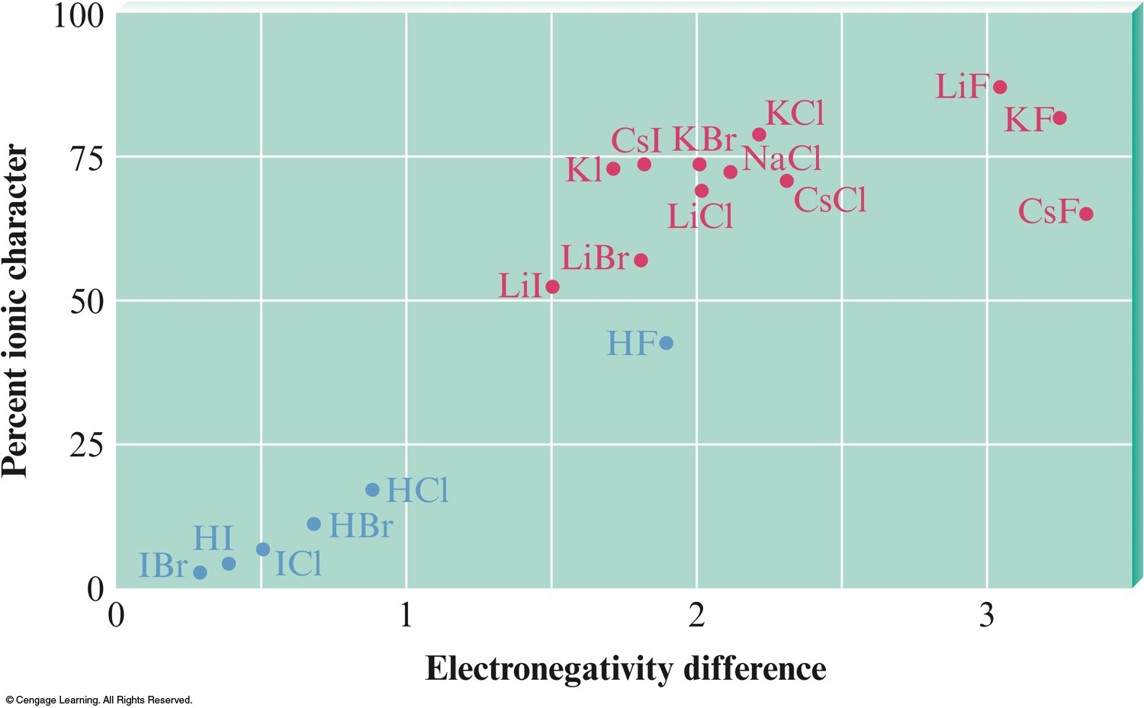
Partial Ionic Character of Covalent Bonds

• No bonds reach 100% ionic character even with compounds that have the maximum possible electronegativity difference. $$ \begin{align} \text{% ionic}&\text{ character of a bond} \\ & = \left( \frac{\text{measured dipole moment of X-Y}}{\text{calculated dipole moment of }\chem{X^+Y^+}} \right) \times 100\% \end{align} $$

Ionic Character and Electronegativity

Operational Definition of Ionic Compound

• Any compound that conducts an electric current when melted will be classified as ionic.

The Covalent Chemical Bond: A Model

Models

• Models are attempts to explain how nature operates on the microscopic level based on experiences in the macroscopic world.

Fundamental Properties of Models

1. A model does not equal reality.
2. Models are oversimplifications, and are therefore often wrong.
3. Models become more complicated and are modified as they age.
4. We must understand the underlying assumptions in a model so that we don't misuse it.
5. When a model is wrong, we often learn much more than when it is right.

Covalent Bond Energies and Chemical Reactions

Bond Energies

• To break bonds, energy must be added to the system (endothermic, energy term carries a positive sign).
• To form bonds, energy is released (exothermic, energy term carries a negative sign).

$$ \Delta H = \sum n \times D_\text{bonds broken} - \sum n \times D_\text{bonds formed} $$ \( D \) represents the bond energy per mole of bonds (always has a positive sign).

The Localized Electron Bonding Model

Localized Electron Model

• A molecule is composed of atoms that are bound together by sharing pairs of electrons using the atomic orbitals of the bound atoms.
• Electron pairs are assumed to be localized on a particular atom or in the space between two atoms:
  • Lone pairs – pairs of electrons localized on an atom
  • Bonding pairs – pairs of electrons found in the space between the atoms

Localized Electron Model - What is it?

1. Description of valence electron arrangement (Lewis structure).
2. Prediction of geometry (VSEPR model).
3. Description of atomic orbital types used by atoms to share electrons or hold lone pairs.

Lewis Structures

Lewis Structure

• Shows how valence electrons are arranged among atoms in a molecule.
• Reflects central idea that stability of a compound relates to noble gas electron configuration.

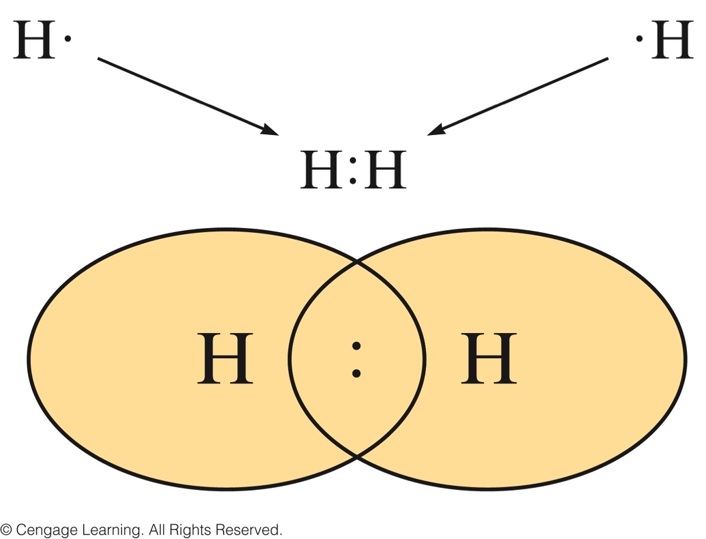
Duet Rule

• Hydrogen forms stable molecules where it shares two electrons.

Octet Rule

• Elements form stable molecules when surrounded by eight electrons.

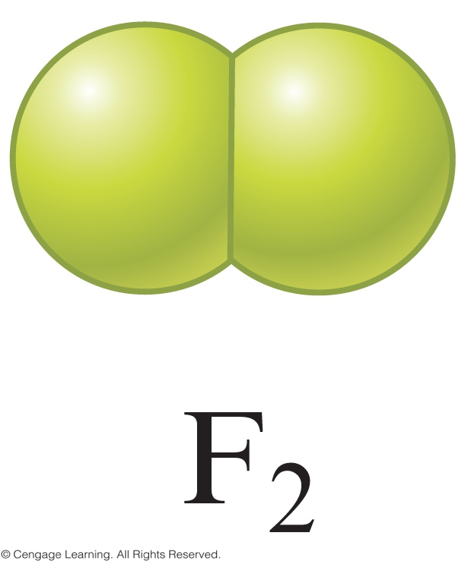
Types of Covalent Bonds

• Single Covalent Bond - A covalent bond in which two atoms share one pair of electrons. $$ \chem{H-H} $$
• Double Covalent Bond - A covalent bond in which two atoms share two pairs of electrons. $$ \chem{O=C=O} $$
• Triple Covalent Bond - A covalent bond in which two atoms share three pairs of electrons. $$ \chem{N\equiv N} $$

Steps for Writing Lewis Structures

1. Sum the valence electrons from all the atoms.
2. Use a pair of electrons to form a bond between each pair of bound atoms.
3. Atoms usually have noble gas configurations. Arrange the remaining electrons to satisfy the octet rule (or duet rule for hydrogen).

Step 1: Sum the valence electrons from all the atoms. (Use the periodic table.)

$$ \text{Example: }\chem{H_2O} $$ $$ 2\left( 1\,e^- \right) + 6 e^- = 8\,e^-\,\text{total} $$

Step 2: Use a pair of electrons to form a bond between each pair of bound atoms.

$$ \text{Example: }\chem{H_2O} $$

Step 3: Atoms usually have noble gas configurations. Arrange the remaining electrons to satisfy the octet rule (or duet rule for hydrogen).

$$ \text{Example: }\chem{H_2O,\, PBr_3, \,and\, HCN} $$

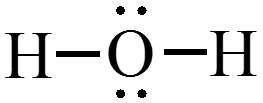
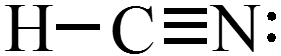
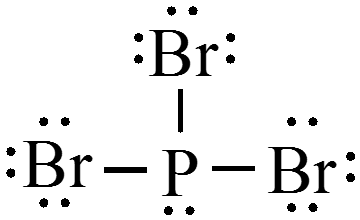
Concept Check 1

Draw a Lewis structure for each of the following molecules:

• \( \chem{H_2} \)
• \( \chem{F_2} \)
• \( \chem{HF} \)
• \( \chem{NH_3} \)
• \( \chem{CO_2} \)
• \( \chem{CCl_4} \)

Exceptions to the Octet Rule

Too Few Electrons

• Boron tends to form compounds in which the boron atom has fewer than eight electrons around it (it does not have a complete octet). $$ \chem{BH_3} = 6e^- $$

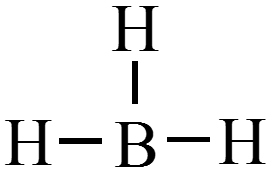
Expanded Octets

• When it is necessary to exceed the octet rule for one of several third-row (or higher) elements, place the extra electrons on the central atom. $$ \chem{SF_4} = 34e^- $$ 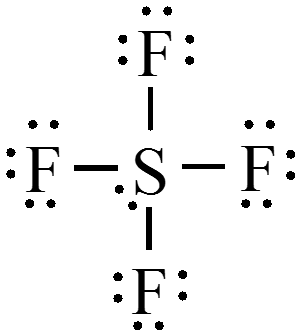$$ \chem{AsBr_5} = 40e^- $$

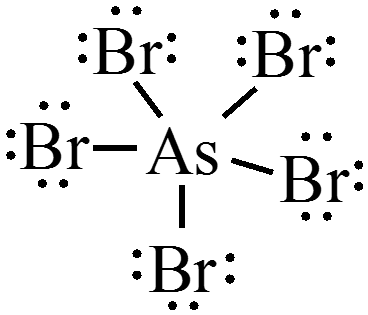
Concept Check 2

Draw a Lewis structure for each of the following molecules:

• \( \chem{BF_3} \)
• \( \chem{PCl_5} \)
• \( \chem{SF_6} \)

Let's Review

• C, N, O, and F should always be assumed to obey the octet rule.
• B and Be often have fewer than 8 electrons around them in their compounds.
• Second-row elements never exceed the octet rule.
• Third-row and heavier elements often satisfy the octet rule but can exceed the octet rule by using their empty valence d orbitals.
• When writing the Lewis structure for a molecule, satisfy the octet rule for the atoms first. If electrons remain after the octet rule has been satisfied, then place them on the elements having available d orbitals (elements in Period 3 or beyond).

Resonance

• More than one valid Lewis structure can be written for a particular molecule.
• Actual structure is an average of the resonance structures.
• Electrons are really delocalized – they can move around the entire molecule. $$ \chem{NO_3^-} = 24 e^- $$

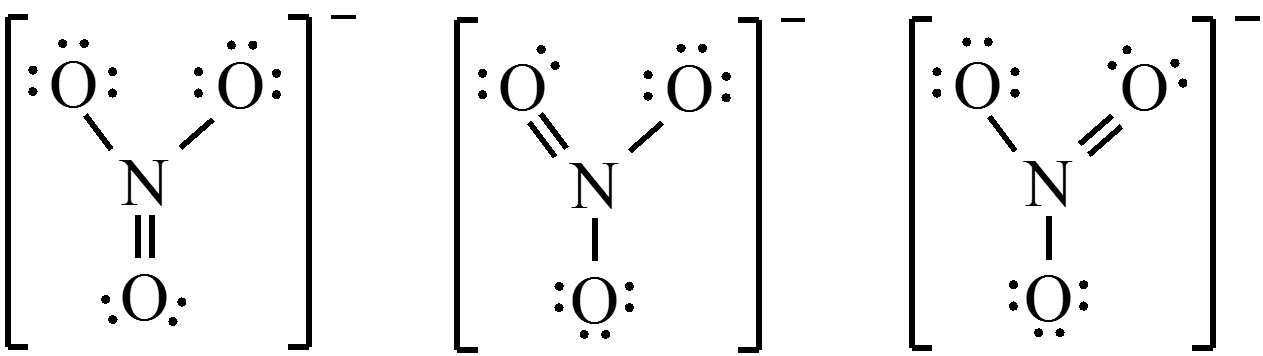
Concept Check 3

Draw a Lewis structure for each of the following molecules:

• \( \chem{CO} \)
• \( \chem{CO_2} \)
• \( \chem{CH_3OH} \)
• \( \chem{OCN^-} \)

Formal Charge

• Used to evaluate nonequivalent Lewis structures.
• Atoms in molecules try to achieve formal charges as close to zero as possible.
• Any negative formal charges are expected to reside on the most electronegative atoms.
• Formal charge = (# valence \(e^–\) on free neutral atom) – (# valence \(e^–\) assigned to the atom in the molecule).
• Assume:
  • Lone pair electrons belong entirely to the atom in question.
  • Shared electrons are divided equally between the two sharing atoms.

Rules Governing Formal Charge

• To calculate the formal charge on an atom:
  1. Take the sum of the lone pair electrons and one-half the shared electrons.
  2. Subtract the number of assigned electrons from the number of valence electrons on the free, neutral atom.
• The sum of the formal charges of all atoms in a given molecule or ion must equal the overall charge on that species.
• If nonequivalent Lewis structures exist for a species, those with formal charges closest to zero and with any negative formal charges on the most electronegative atoms are considered to best describe the bonding in the molecule or ion.

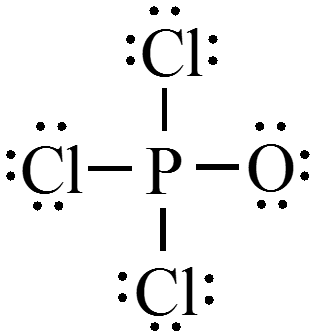
Concept Check 4

Consider the Lewis structure for \(\chem{POCl_3}\). Assign the formal charge for each atom in the molecule.

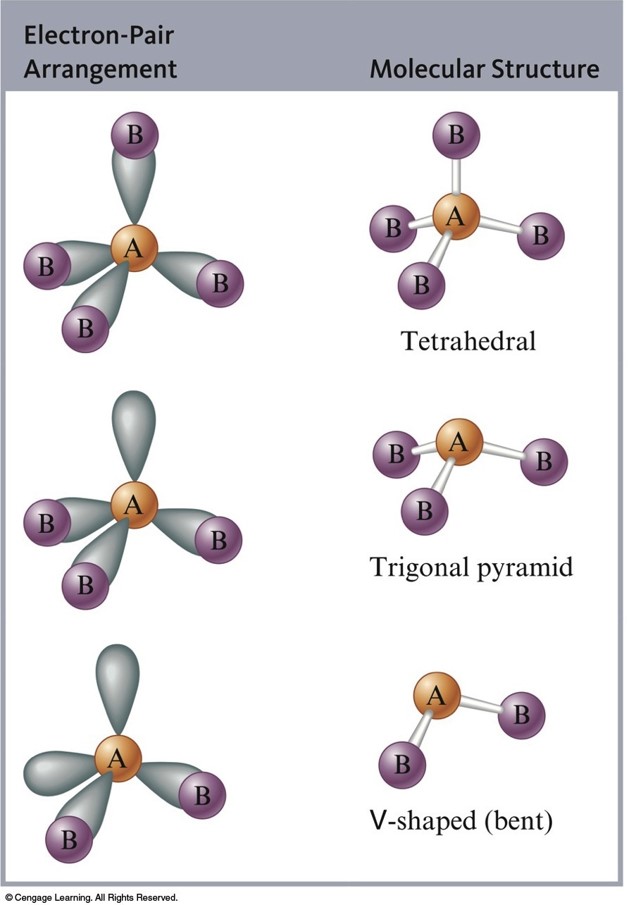
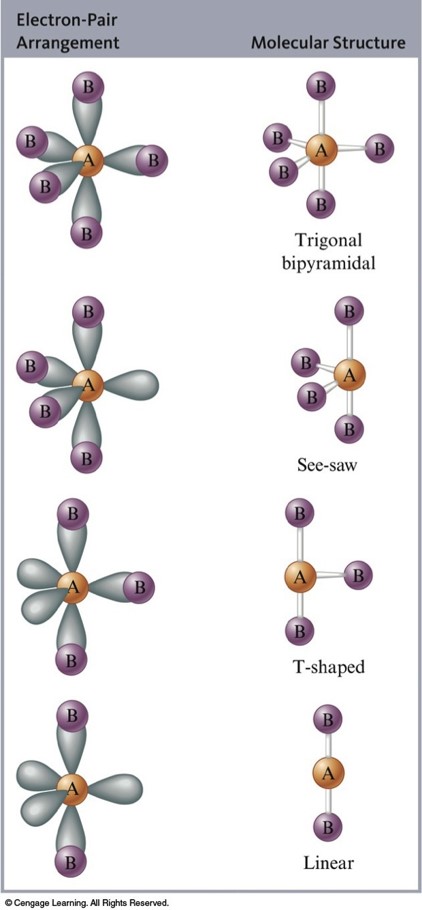
Molecular Structure: The VSEPR Model

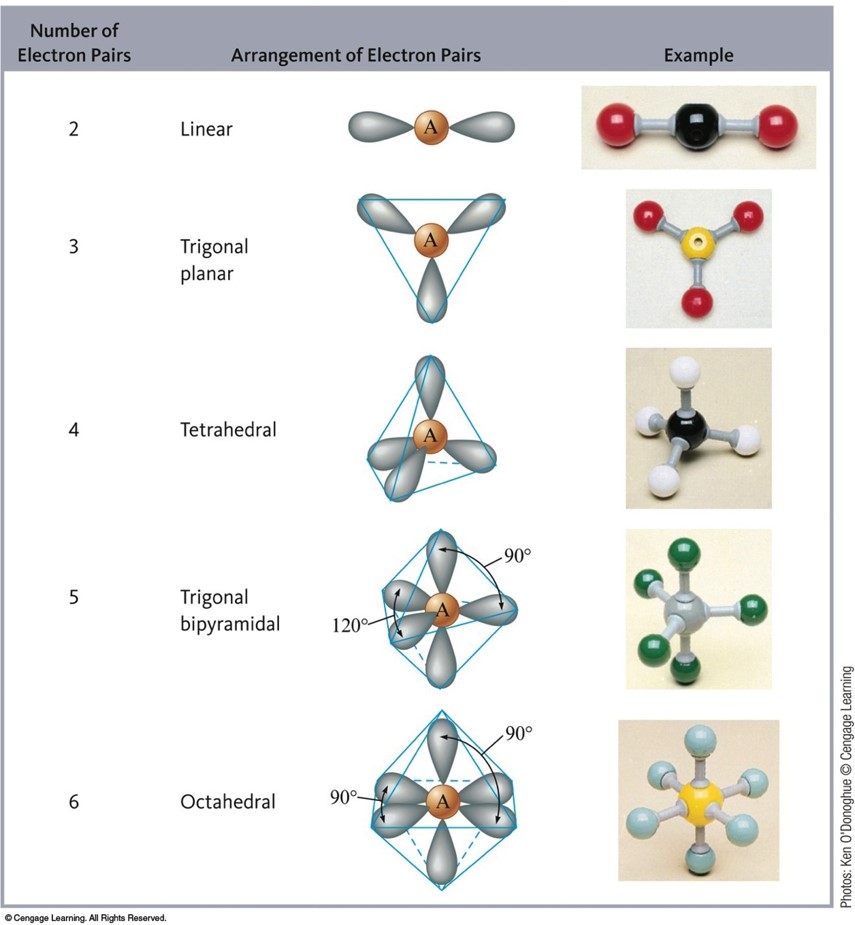
VSEPR Model

• VSEPR: Valence Shell Electron-Pair Repulsion.
• The structure around a given atom is determined principally by minimizing electron pair repulsions.

Steps to Apply the VSEPR Model

1. Draw the Lewis structure for the molecule.
2. Count the electron pairs and arrange them in the way that minimizes repulsion (put the pairs as far apart as possible.
3. Determine the positions of the atoms from the way electron pairs are shared (how electrons are shared between the central atom and surrounding atoms).
4. Determine the name of the molecular structure from positions of the atoms.

Arrangements of Electrons Around an Atom Yielding Minimum Repulsion

Structures of Molecules That Have Four Electron Pairs Around the Central Atom

Structures of Molecules with Five Electron Pairs Around the Central Atom