Chapter 6

Electronic Structure and Periodic Properties of Elements

Shaun Williams, PhD

Electromagnetic Radiation

Different Colored Fireworks

Questions to Consider

Why do we get colors?
Why do different chemicals give us different colors?

Various colored fireworks bursting over Washington DC landmarks.

Electromagnetic Radiation

One of the ways that energy travels through space.
Three characteristics:
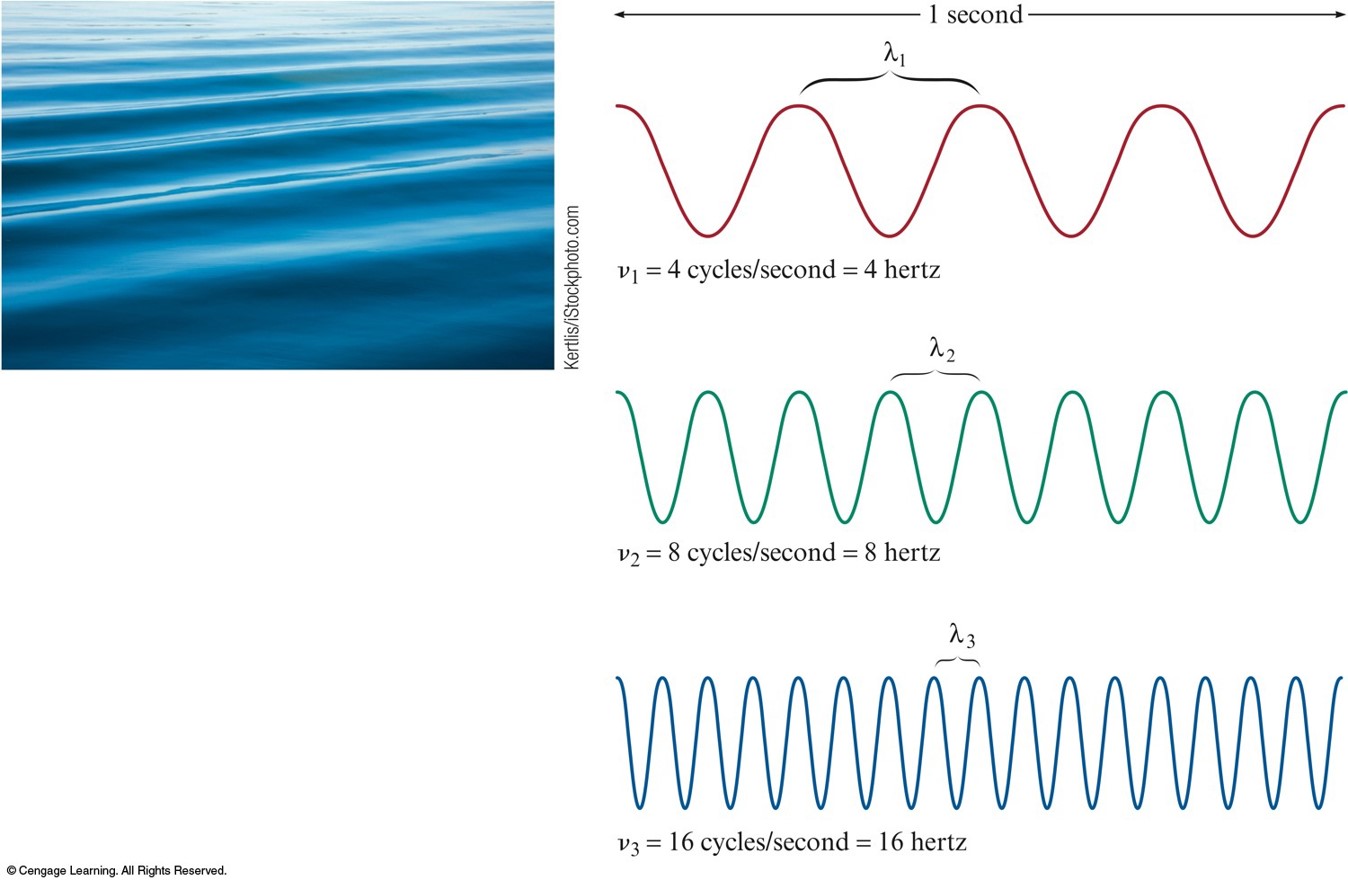
- Wavelength ($\lambda$) - distance between two consecutive peaks or troughs in a wave.
- Frequency ($\nu$) - number of waves (cycles) per second that pass a given point in space
- Speed ($c$) - speed of light ($2.9979\times 10^8\,\bfrac{\text{m}}{\text{s}}$)

$$ c = \lambda \nu $$

Waves

a photograph of waves on the surface of water. A graphic of three waves whose wavelengths start long and then are divided by one-half and then one-half again. As the wavelength is halved, the frequency doubles.

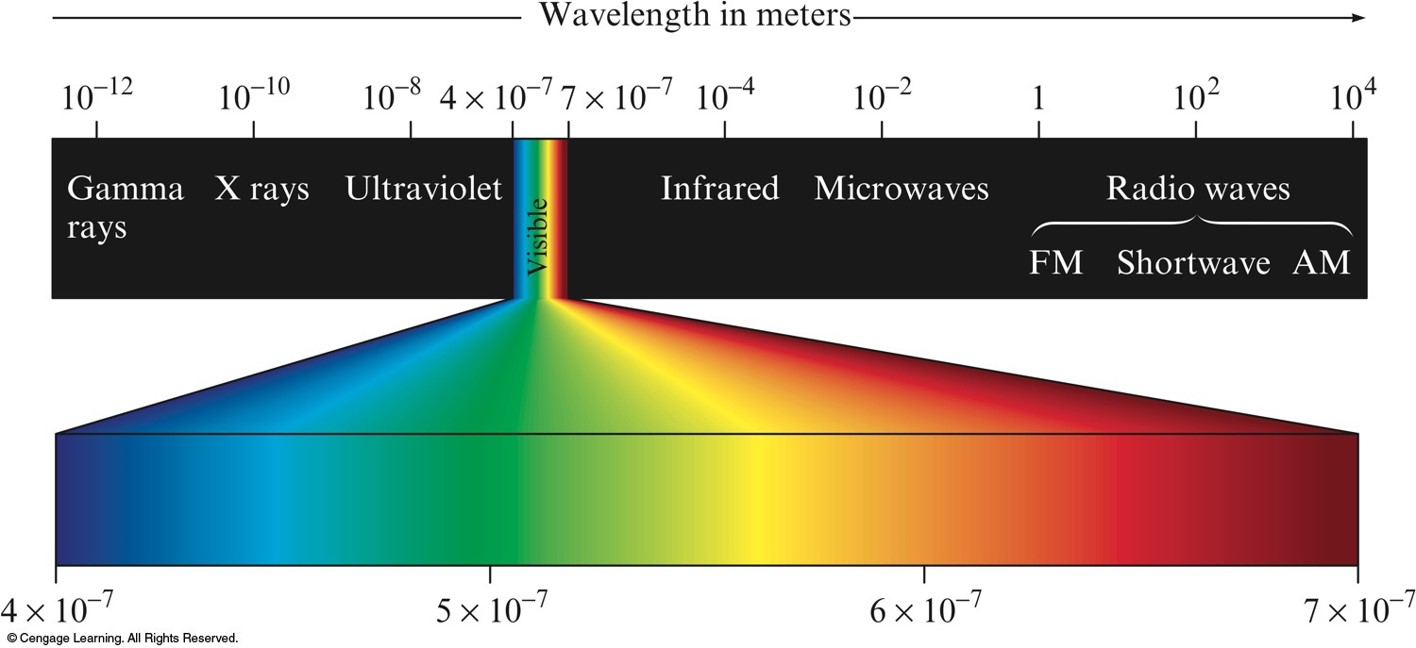
Classification of Electromagnetic Radiation

The breakdown of the electromagnetic radiation into the regions gamma rays, x rays, ultraviolty, visible, infrared, microwaves, and radio waves (from high energy to low energy).

Pickle Light

When electricity is passed through a pickle, it glows with a yellow light.

The Nature of Matter

Energy can be gained or lost only in whole number multiples of $h\nu$.
A system can transfer energy only in whole quanta (or "packets").
Energy seems to have particulate properties too.
Energy is quantized.
Electromagnetic radiation is a stream of "particles" called photons. $$ E_\text{photon} = h\nu = \frac{hc}{\lambda} $$
Planck's constant = $h = 6.626 \times 10^{-34}\,\chem{J\cdot s}$

Energy

Energy has mass $E=mc^2$
Dual nature of light:
- Electromagnetic radiation (and all matter) exhibits wave properties and particulate properties.

The Atomic Spectrum of Hydrogen

Continuous spectrum (results when white light is passed through a prism) - contains all the wavelengths of visible light
Line spectrum - each line corresponds to a discrete wavelength:
- Hydrogen emission spectrum

Significance

Only certain energies are allowed for the electron in the hydrogen atom.
Energy of the electron in the hydrogen atom is quantized.

The Bohr Model

Electron in a hydrogen atom moves around the nucleus only in certain allowed circular orbits.
Bohr's model gave hydrogen atom energy levels consistent with the hydrogen emission spectrum.
Ground state - lowest possible energy state ($n = 1$)

Electronic Transitions in the Bohr Model for the Hydrogen Atom

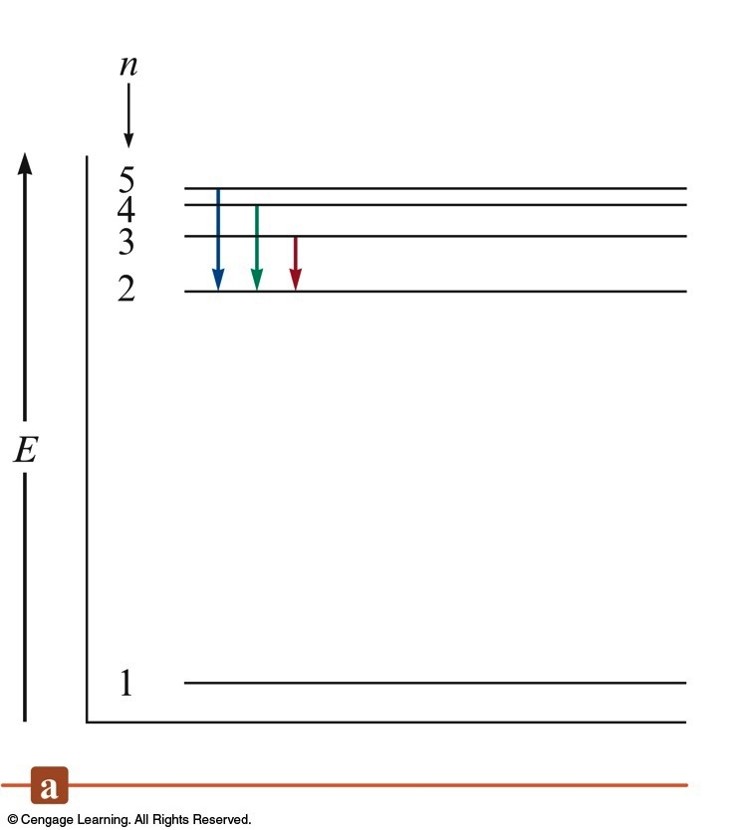
A graphical representation of the first five energy levels in the hydrogen atom. The levels get closer together as the energy increases.

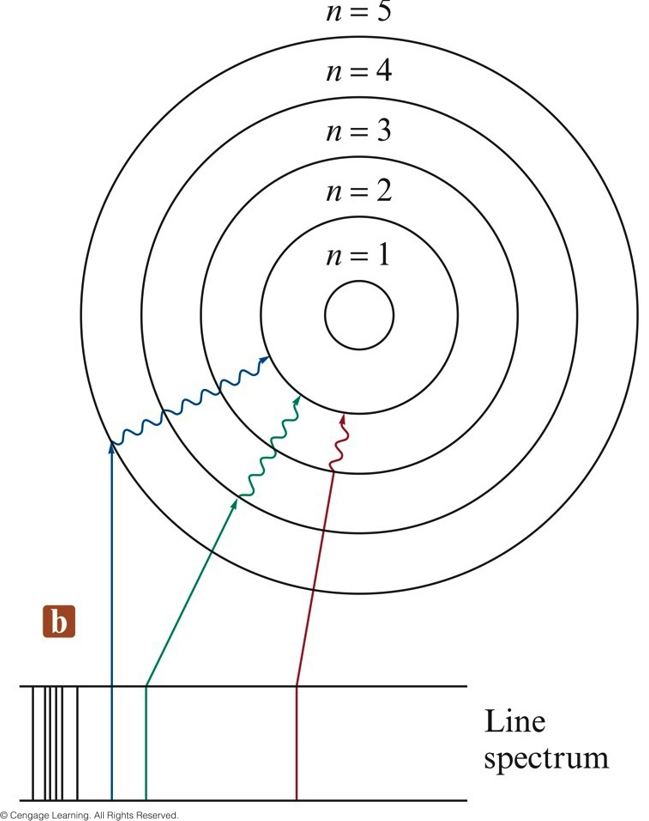
The first five orbits of the hydrogen atom (per the Bohr model) and the electron transition between the 5-to-2, 4-to-2, and 3-to-2 which are responsible for the blue line, green line, and red line in the hydrogen line spectrum.

The Bohr Model Energy Equation

For a single electron transition from one energy level to another: $$ \Delta E = -2.178 \times 10^{-18}\,\chem{J} \left( \frac{1}{n_\text{final}^2} - \frac{1}{n_\text{initial}^2} \right) $$
- $\Delta E$ = change in energy of the atom (energy of the emitted photon)
- $n_\text{final}$ = integer; final distance from the nucleus
- $n_\text{initial}$ = integer; initial distance from the nucleus

The Bohr Model Analysis

The model correctly fits the quantized energy levels of the hydrogen atom and postulates only certain allowed circular orbits for the electron.
As the electron becomes more tightly bound, its energy becomes more negative relative to the zero-energy reference state (free electron). As the electron is brought closer to the nucleus, energy is released from the system.
Bohr's model is incorrect. This model only works for hydrogen.
Electrons move around the nucleus in circular orbits.

The Quantum Mechanical Model of the Atom

We do not know the detailed pathway of an electron.
Heisenberg uncertainty principle:
- There is a fundamental limitation to just how precisely we can know both the position and momentum of a particle at a given time. $$ \Delta x \cdot \Delta \left( mv \right) \ge \frac{h}{2\pi} $$
  - $\Delta x$ = uncertainty in a particle's position
  - $\Delta (mν)$ = uncertainty in a particle's momentum
  - $h$ = Planck's constant

Physical Meaning of a Wave Function $(\Psi)$

The square of the function indicates the probability of finding an electron near a particular point in space.
- Probability distribution – intensity of color is used to indicate the probability value near a given point in space.

Probability Distribution for the 1s Wave Function

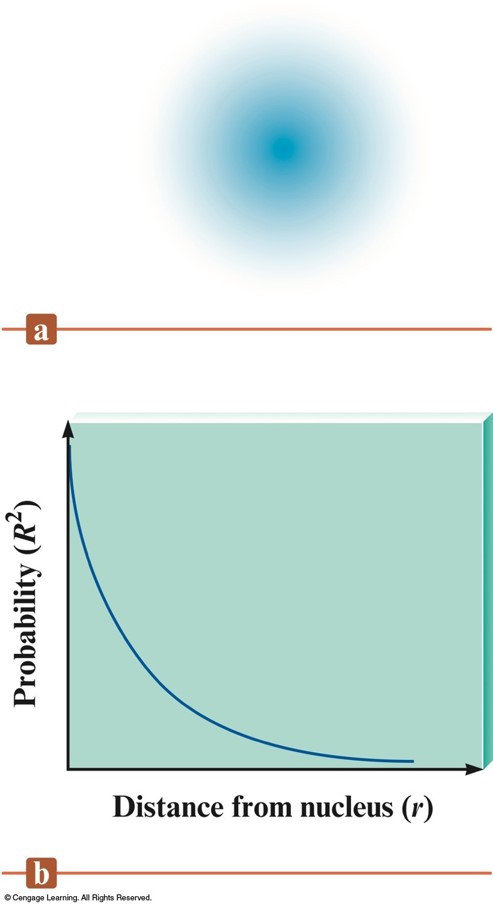
Plots of the 1s orbital with high density at the center and exponentially less as the distance from the center increases.

Radial Probability Distribution

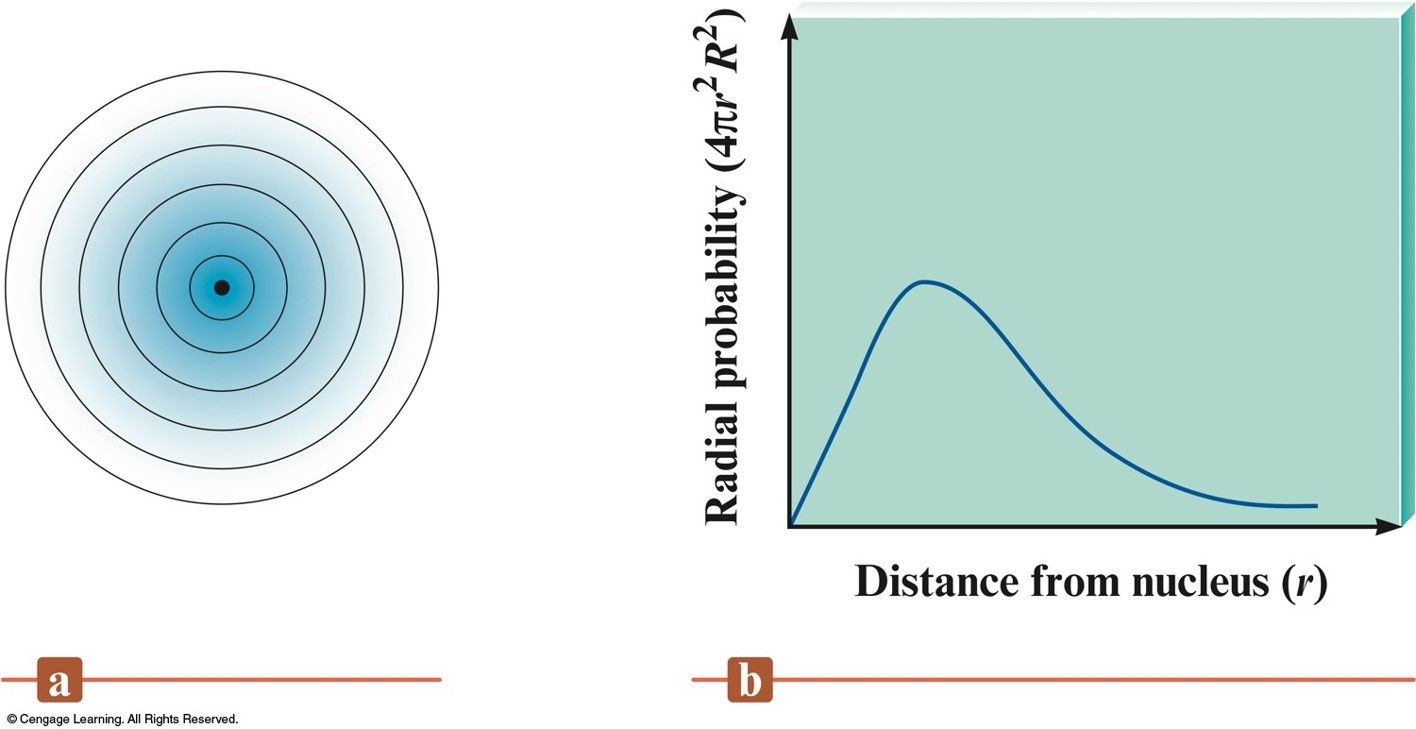
The radial probability distribution with no intensity at the center, rising steeply to a max and the exponentially dropping.

Relative Orbital Size

Difficult to define precisely.
Orbital is a wave function.
Picture an orbital as a three-dimensional electron density map.
Hydrogen 1s orbital:
- Radius of the sphere that encloses 90% of the total electron probability.

Quantum Numbers

Principal quantum number ($n$) – size and energy of the orbital.
Angular momentum quantum number ($l$) – shape of atomic orbitals (sometimes called a subshell).
Magnetic quantum number ($m_l$) – orientation of the orbital in space relative to the other orbitals in the atom.

Quantum Numbers for the First Four Levels of Orbitals in the Hydrogen Atom

$n$	$l$	Sublevel Designation	$m_l$	Number of Orbitals
1	0	$1s$	0	1
2	0	$2s$	0	1
2	1	$2p$	-1,0,+1	3
3	0	$3s$	0	1
	1	$3p$	-1,0,+1	3
	2	$3d$	-2,-1,0,+1,+2	5
4	0	$4s$	0	1
	1	$4p$	-1,0,+1	3
	2	$4d$	-2,-1,0,+1,+2	5
	3	$4f$	-3,-2,-1,0,+1,+2,+3	7

Exercise 1

For principal quantum level $n = 3$, determine the number of allowed subshells (different values of $l$), and give the designation of each.

Exercise 1 - Answer

For principal quantum level $n = 3$, determine the number of allowed subshells (different values of $l$), and give the designation of each.

Number of allowed subshells = 3 ($l=0,1,2$)

Orbital Shapes and Energies

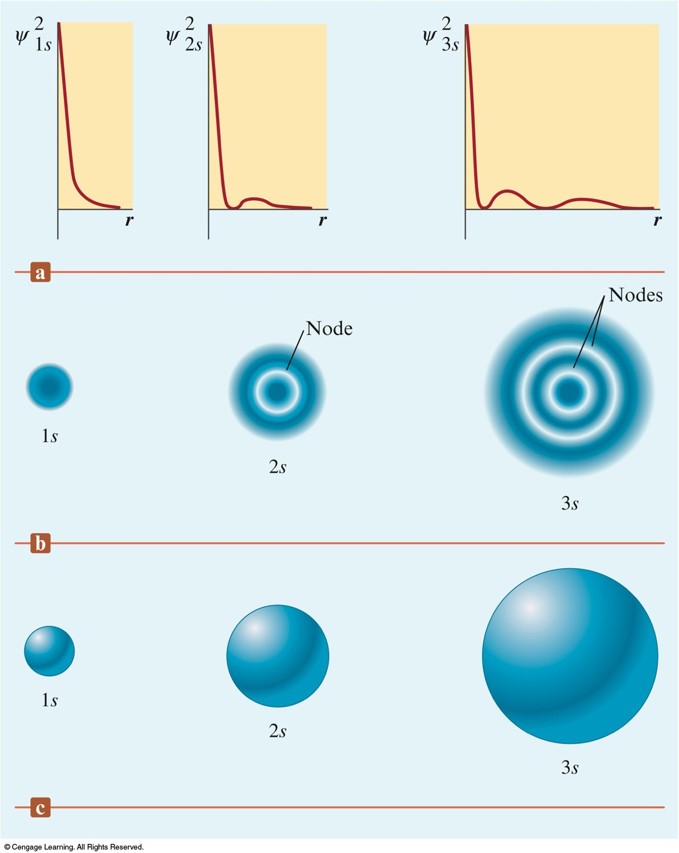
Three Representations of the Hydrogen $1s$, $2s$, and $3s$ Orbitals

Plots of the three orbitals, density plots, and 3D plots.

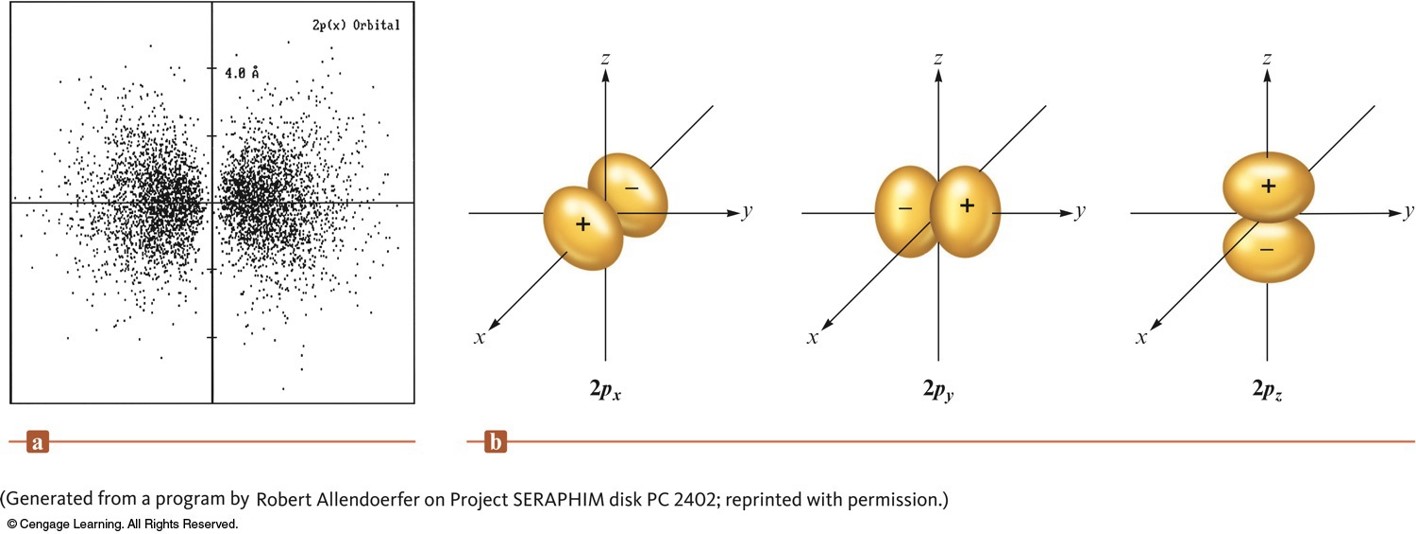
The Boundary Surface Representations of All Three $2p$ Orbitals

A density plot of one of the 2p orbitals and 3D plots of all three 2p orbtials showing the lobe structure of the orbitals.

The Boundary Surfaces of All of the $3d$ Orbitals

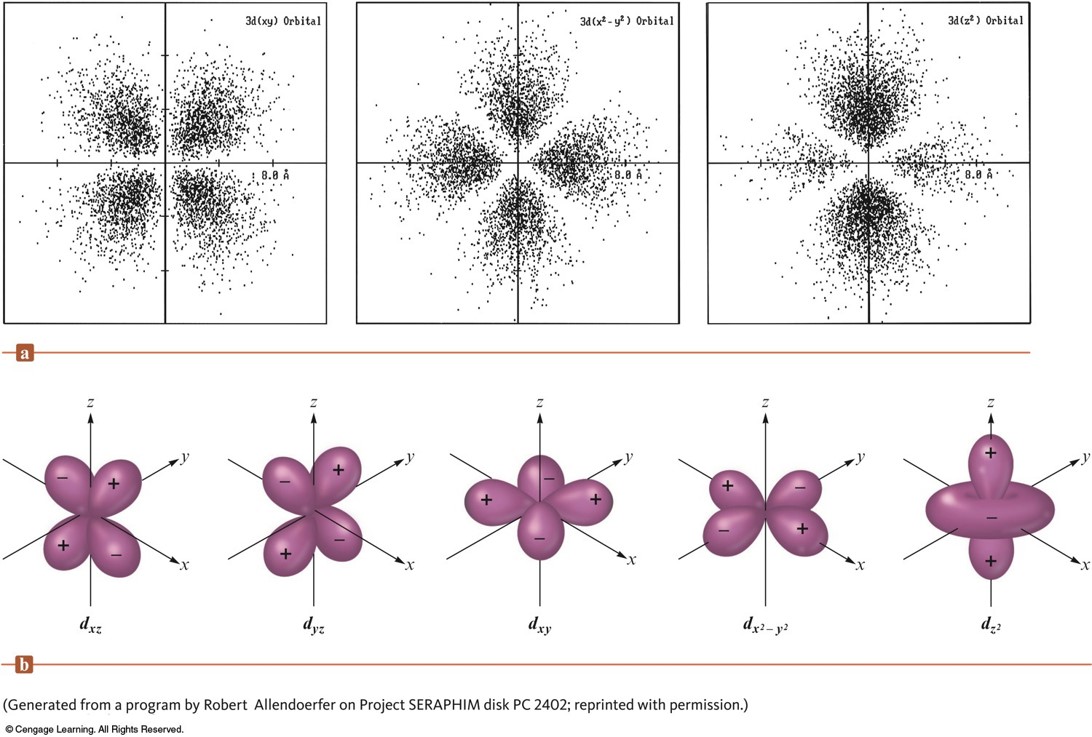
Density plots of three of the 3d orbitals and 3D plots of all five 3d orbtials showing the double lobe structure of the orbitals.

Representation of the $4f$ Orbitals in Terms of Their Boundary Surfaces

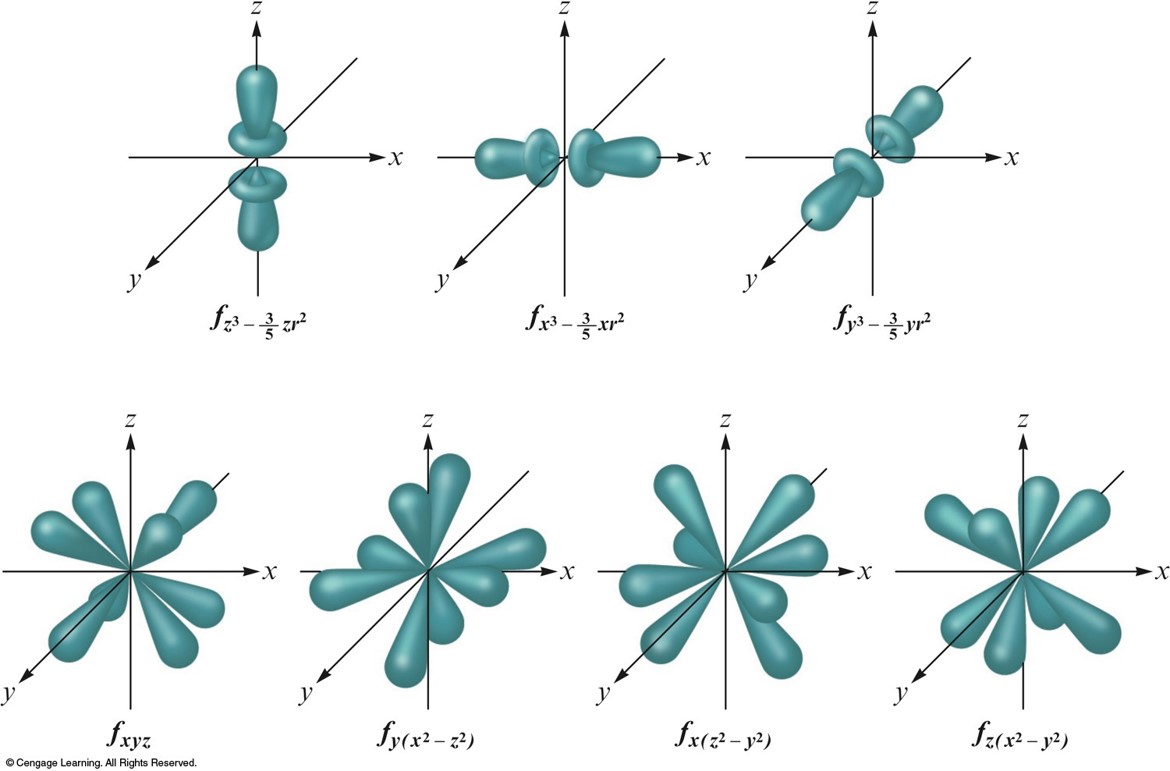
3D plots of all seven 4f orbtials showing the quadruple lobe structure of the orbitals.

Electron Spin and the Pauli Principle

Electron Spin

Electron spin quantum number ($m_s$) - can be $+\bfrac{1}{2}$ or $-\bfrac{1}{2}$.
Pauli exclusion principle - in a given atom no two electrons can have the same set of four quantum numbers.
An orbital can hold only two electrons, and they must have opposite spins.

Polyelectronic Atoms

Atoms with more than one electron.
Electron correlation problem:
- Since the electron pathways are unknown, the electron repulsions cannot be calculated exactly.
When electrons are placed in a particular quantum level, they "prefer" the orbitals in the order $s$, $p$, $d$, and then $f$.

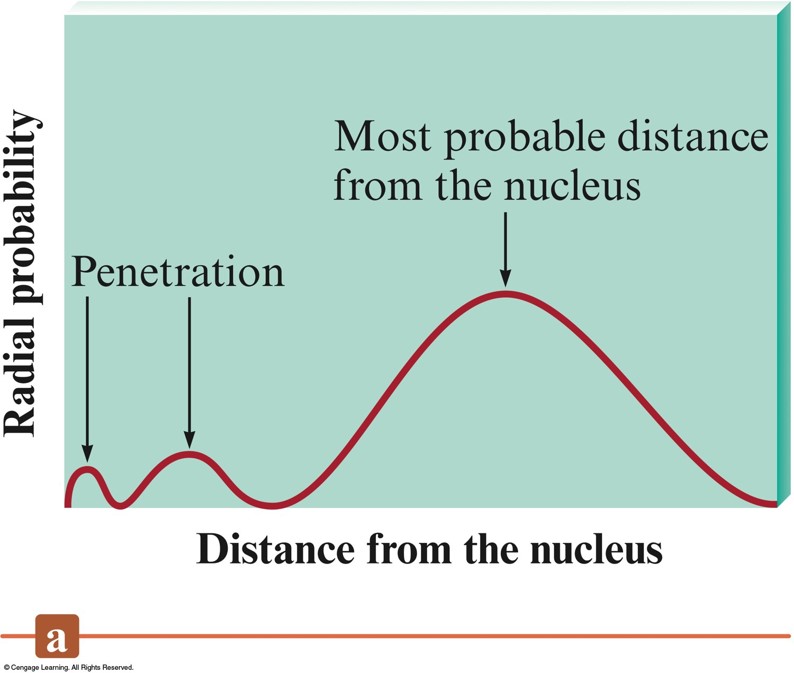
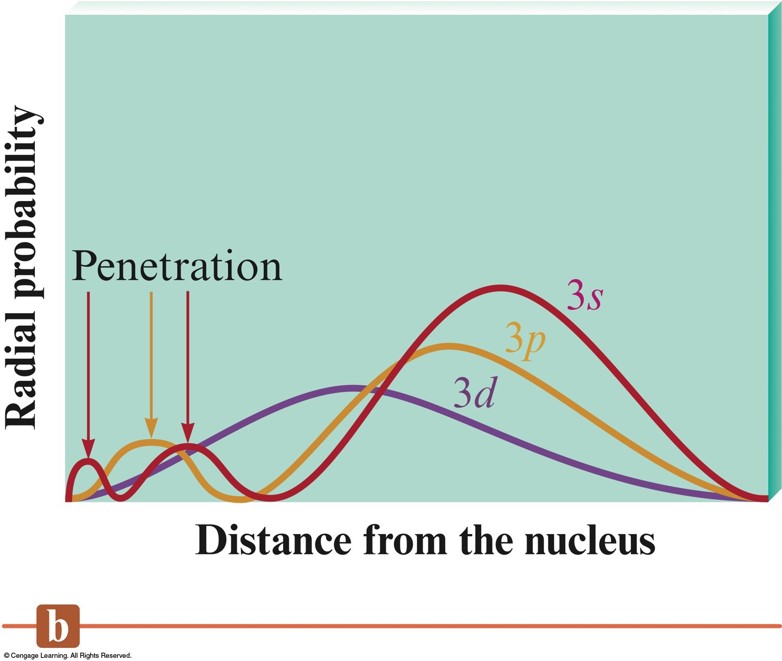
Penetration Effect

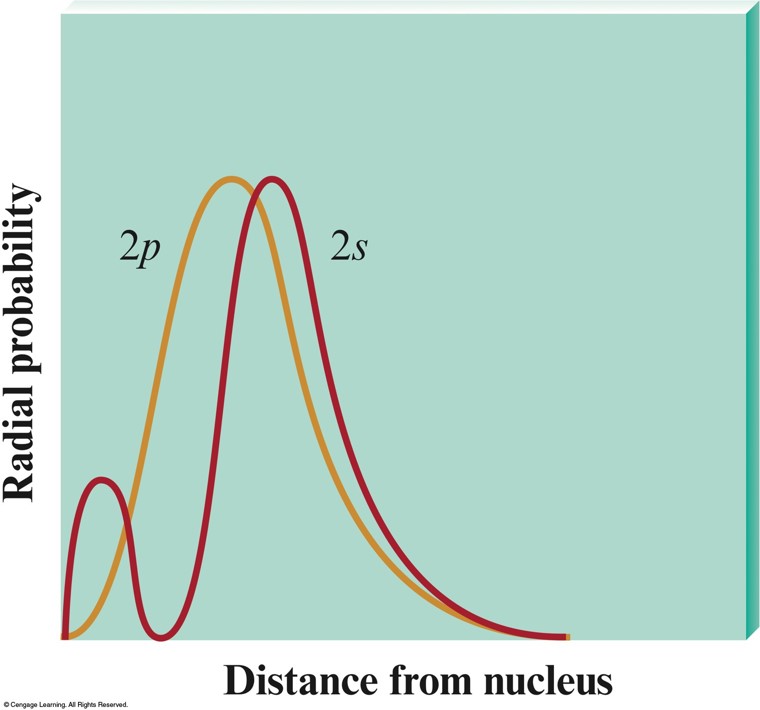
A $2s$ electron penetrates to the nucleus more than one in the $2p$ orbital.
This causes an electron in a $2s$ orbital to be attracted to the nucleus more strongly than an electron in a $2p$ orbital.
Thus, the $2s$ orbital is lower in energy than the $2p$ orbitals in a polyelectronic atom.

A Comparison of the Radial Probability Distributions of the $2s$ and $2p$ Orbitals

The plots of the 2s and 2p orbitals shows the small penetration bump in the 2s that makes the 2s more stable than the 2p.

The Radial Probability Distribution of the $3s$ Orbital

The radial plot of the 3s orbital shows two small penetration bumps insidethe most probable distance from the nucleus for the 3s orbital.

A Comparison of the Radial Probability Distributions of the $3s$, $3p$, and $3d$ Orbitals

The plots of the 3s, 3p, and 3d orbitals shows the penetration bumps that make the 3s the most stable followed by the 3p.

The History of the Periodic Table

Originally constructed to represent the patterns observed in the chemical properties of the elements.
Mendeleev is given the most credit for the current version of the periodic table because he emphasized how useful the periodic table could be in predicting the existence and properties of still unknown elements.

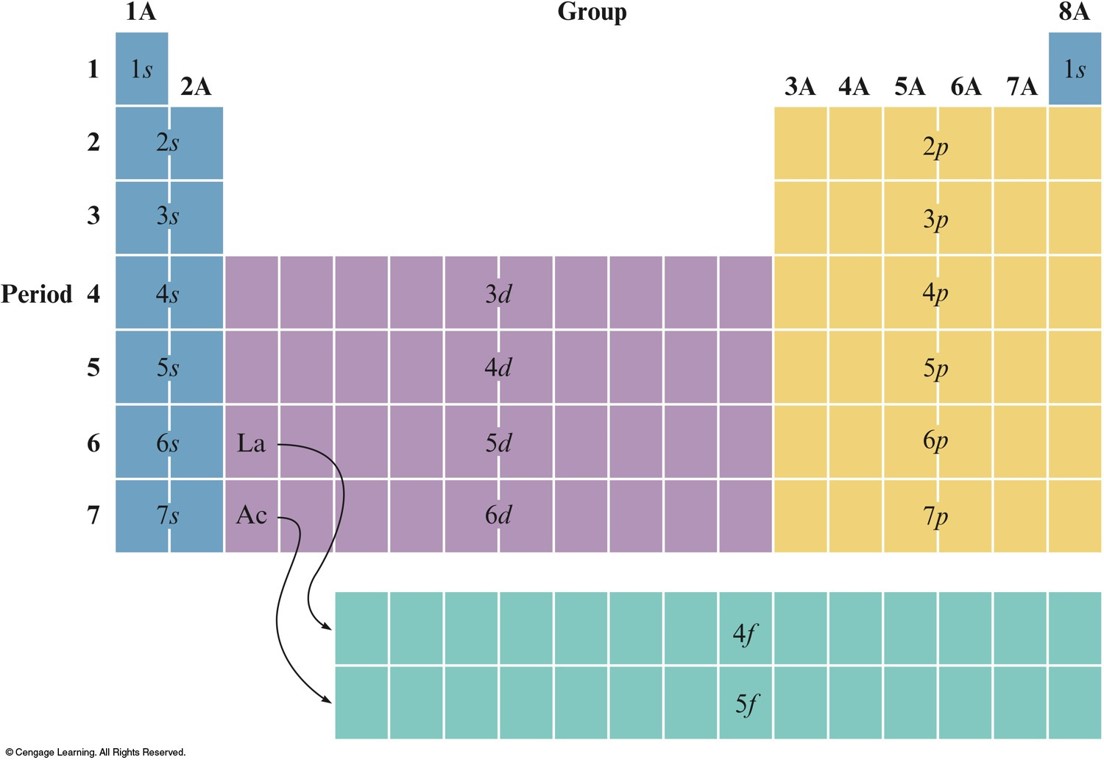
The Aufbau Principle and the Periodic Table

Aufbau Principle

As protons are added one by one to the nucleus to build up the elements, electrons are similarly added to hydrogen-like orbitals.
An oxygen atom has an electron arrangement of two electrons in the $1s$ subshell, two electrons in the $2s$ subshell, and four electrons in the $2p$ subshell.

Oxygen: $1s^22s^22p^4$

Hund's Rule

The lowest energy configuration for an atom is the one having the maximum number of unpaired electrons allowed by the Pauli principle in a particular set of degenerate (same energy) orbitals.

Orbital Diagram

A notation that shows how many electrons an atom has in each of its occupied electron orbitals.

Oxygen: $1s^22s^22p^4$

$1s$	$\phantom{2s}$	$2s$	$\phantom{2s}$		$2p$
$\uparrow\downarrow$	$\phantom{\uparrow\downarrow}$	$\uparrow\downarrow$	$\phantom{\uparrow\downarrow}$	$\uparrow\downarrow$	$\uparrow\phantom{\downarrow}$	$\uparrow\phantom{\downarrow}$

Valence Electrons

The electrons in the outermost principal quantum level of an atom. $1s^22s^22p^6$ (valence electrons = 8)
The elements in the same group on the periodic table have the same valence electron configuration.

The Orbitals Being Filled for Elements in Various Parts of the Periodic Table

The s-block, p-block, d-block, and f-block on the periodic table.

Exercise 2

Determine the expected electron configurations for each of the following.

S
Ba
Eu

Exercise 2 - Answer

Determine the expected electron configurations for each of the following.

S - $1s^22s^22p^63s^23p^4$ or $[\chem{Ne}]3s^23p^4$
Ba - $[\chem{Xe}]6s^2$
Eu - $[\chem{Xe}]6s^24f^7$

Periodic Trends in Atomic Properties

Periodic Trends

Ionization Energy
Electron Affinity
Atomic Radius

Ionization Energy

Energy required to remove an electron from a gaseous atom or ion.
- $X(g)\rightarrow X^+(g)+e^-$

$\chem{Mg\rightarrow Mg^+ + e^-}$	$I_1=735\,\bfrac{\chem{kJ}}{\chem{mol}}$	(1^st IE)
$\chem{Mg^+\rightarrow Mg^{2+} + e^-}$	$I_2=1445\,\bfrac{\chem{kJ}}{\chem{mol}}$	(2^nd IE)
$\chem{Mg^{2+}\rightarrow Mg^{3+} + e^-}$	$I_3=7730\,\bfrac{\chem{kJ}}{\chem{mol}}$	(3^rd IE)*

* Core electrons are bound much more tightly than valence electrons.

More on Ionization Energy

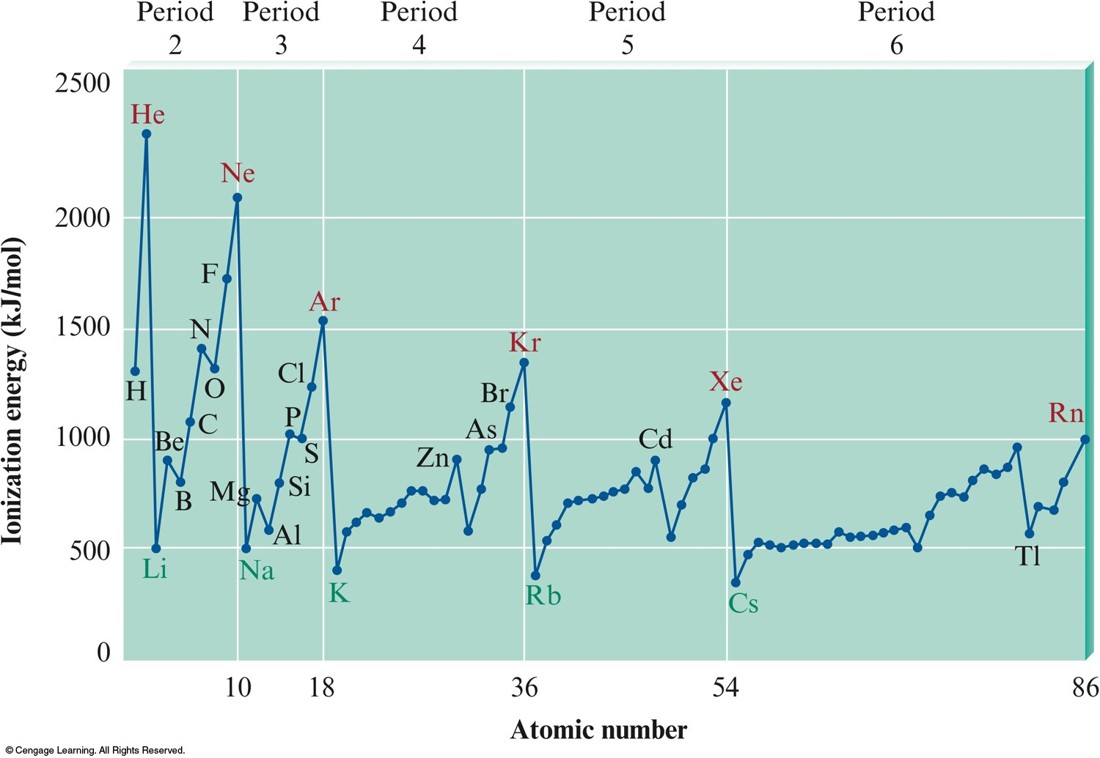
In general, as we go across a period from left to right, the first ionization energy increases.
Why?
- Electrons added in the same principal quantum level do not completely shield the increasing nuclear charge caused by the added protons.
- Electrons in the same principal quantum level are generally more strongly bound from left to right on the periodic table.
In general, as we go down a group from top to bottom, the first ionization energy decreases.
Why?
- The electrons being removed are, on average, farther from the nucleus.

The Values of First Ionization Energy for the Elements in the First Six Periods

Plot of the ionizations of the elements in the first six rows showing the trends described on the previous slide.

Successive Ionization Energies (kJ per Mole) for the Elements in Period 3

Element	$I_1$	$I_2$	$I_3$	$I_4$	$I_5$	$I_6$	$I_7$
Na	495	4560
Mg	735	1445	7730
Al	580	1815	2740	11600
Si	780	1575	3220	4350	16100
P	1060	1890	2905	4950	6270	21200
S	1005	2260	3375	4565	6950	8490	27000
Cl	1255	2295	3850	5160	6560	9360	11000
Ar	1527	2665	3945	5770	7230	8780	12000

Electron Affinity

Energy change associated with the addition of an electron to a gaseous atom.
- $\chem{X(g) + e^– \rightarrow X^–(g)}$
In general as we go across a period from left to right, the electron affinities become more negative.
In general electron affinity becomes more positive in going down a group.

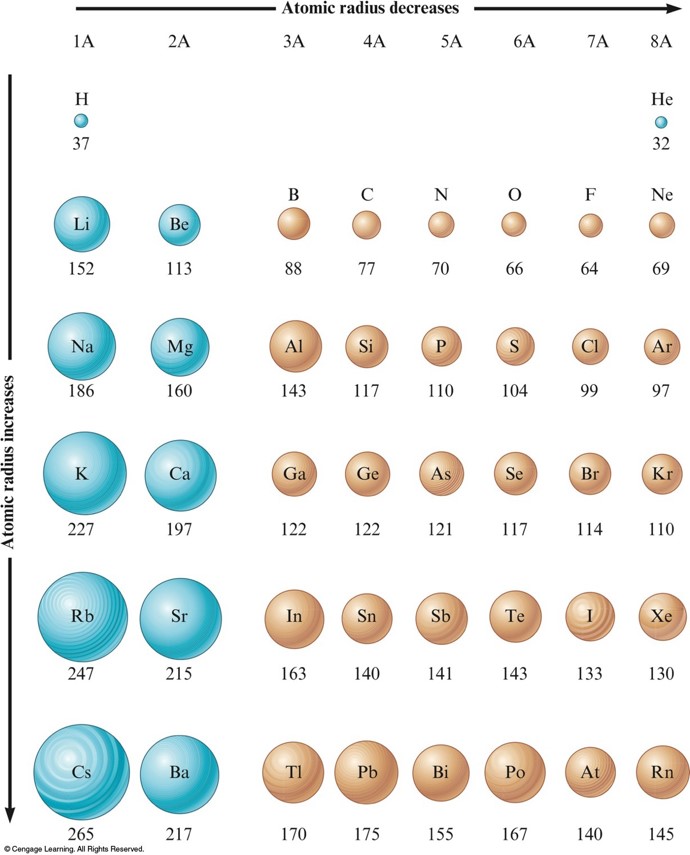
Atomic Radius

In general as we go across a period from left to right, the atomic radius decreases.
- Effective nuclear charge increases, therefore the valence electrons are drawn closer to the nucleus, decreasing the size of the atom.
In general atomic radius increases in going down a group.
- Orbital sizes increase in successive principal quantum levels.

Atomic Radii for Selected Atoms

Plot of the atomic radii of the elements showing the trends described on the previous slide.

Exercise 3

Arrange the elements oxygen, fluorine, and sulfur according to increasing:

Ionization energy
Atomic size

Exercise 3 - Answer

Arrange the elements oxygen, fluorine, and sulfur according to increasing:

Ionization energy - $ \chem{S,O,F} $
Atomic size - $ \chem{F,O,S} $

The Properties of a Group: The Alkali Metals

The Periodic Table - Final Thoughts

It is the number and type of valence electrons that primarily determine an atom's chemistry.
Electron configurations can be determined from the organization of the periodic table.
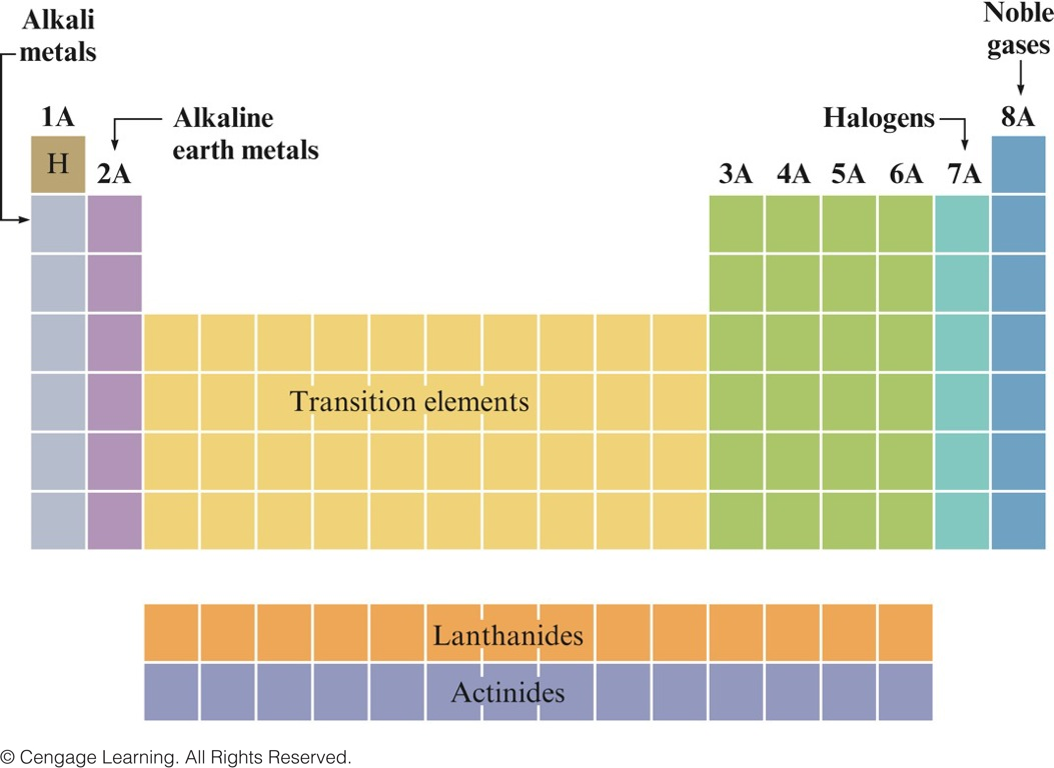
Certain groups in the periodic table have special names.

Special Names for Groups in the Periodic Table

Group names in the periodic table. Group 1 are the alkali metals, group 2 are the alkaline earth metals, group 17 are the halogens, and group 18 are the noble gases.

The Periodic Table - Final Thoughts (cont.)

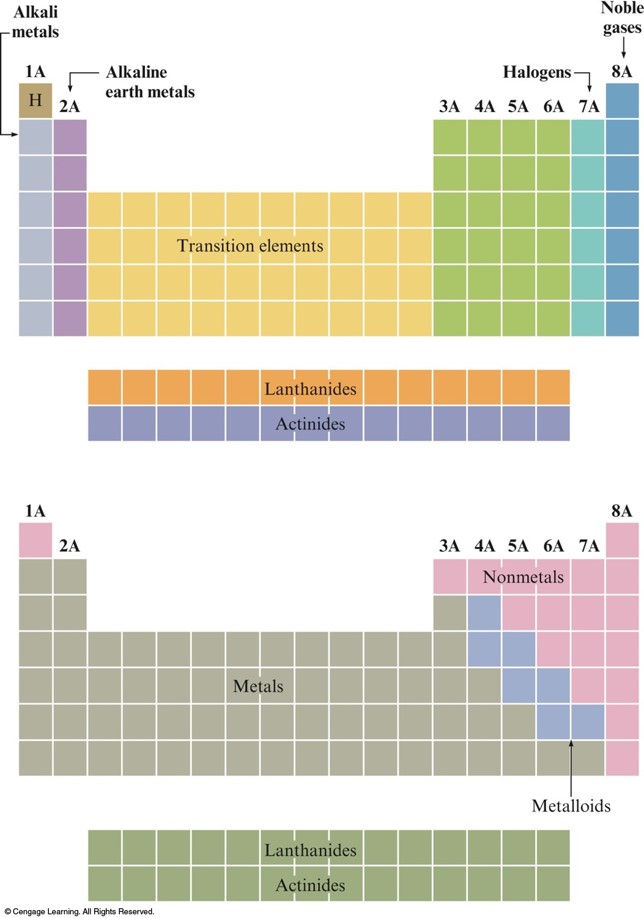
Basic division of the elements in the periodic table is into metals and nonmetals.

The nonmetals at above and to the right of the stair-step line. The metals are to the left and below the stair-step line. The metalloids are seven elements that lie on the stair-step line.

The Alkali Metals

$\chem{Li}$, $\chem{Na}$, $\chem{K}$, $\chem{Rb}$, $\chem{Cs}$, and $\chem{Fr}$
- Most chemically reactive of the metals
  - React with nonmetals to form ionic solids
- Going down group:
  - Ionization energy decreases
  - Atomic radius increases
  - Density increases
  - Melting and boiling points smoothly decrease

\(n\)	\(l\)	Sublevel Designation	\(m_l\)	Number of Orbitals
1	0	\(1s\)	0	1
2	0	\(2s\)	0	1
2	1	\(2p\)	-1,0,+1	3
3	0	\(3s\)	0	1
	1	\(3p\)	-1,0,+1	3
	2	\(3d\)	-2,-1,0,+1,+2	5
4	0	\(4s\)	0	1
	1	\(4p\)	-1,0,+1	3
	2	\(4d\)	-2,-1,0,+1,+2	5
	3	\(4f\)	-3,-2,-1,0,+1,+2,+3	7

\(\chem{Mg\rightarrow Mg^+ + e^-}\)	\(I_1=735\,\bfrac{\chem{kJ}}{\chem{mol}}\)	(1^st IE)
\(\chem{Mg^+\rightarrow Mg^{2+} + e^-}\)	\(I_2=1445\,\bfrac{\chem{kJ}}{\chem{mol}}\)	(2^nd IE)
\(\chem{Mg^{2+}\rightarrow Mg^{3+} + e^-}\)	\(I_3=7730\,\bfrac{\chem{kJ}}{\chem{mol}}\)	(3^rd IE)*

Chapter 6 Electronic Structure and Periodic Properties of Elements

Electromagnetic Radiation

Electromagnetic Radiation

Waves

Classification of Electromagnetic Radiation

Pickle Light

The Nature of Matter

Energy

The Atomic Spectrum of Hydrogen

The Bohr Model

Electronic Transitions in the Bohr Model for the Hydrogen Atom

The Bohr Model Energy Equation

The Bohr Model Analysis

The Quantum Mechanical Model of the Atom

Physical Meaning of a Wave Function \((\Psi)\)

Probability Distribution for the 1s Wave Function

Radial Probability Distribution

Relative Orbital Size

Quantum Numbers

Quantum Numbers for the First Four Levels of Orbitals in the Hydrogen Atom

Exercise 1

Exercise 1 - Answer

Orbital Shapes and Energies

The Boundary Surface Representations of All Three \(2p\) Orbitals

The Boundary Surfaces of All of the \(3d\) Orbitals

Representation of the \(4f\) Orbitals in Terms of Their Boundary Surfaces

Electron Spin and the Pauli Principle

Polyelectronic Atoms

A Comparison of the Radial Probability Distributions of the \(2s\) and \(2p\) Orbitals

The Radial Probability Distribution of the \(3s\) Orbital

A Comparison of the Radial Probability Distributions of the \(3s\), \(3p\), and \(3d\) Orbitals

The History of the Periodic Table

The Aufbau Principle and the Periodic Table

Orbital Diagram

The Orbitals Being Filled for Elements in Various Parts of the Periodic Table

Exercise 2

Exercise 2 - Answer

Periodic Trends in Atomic Properties

Ionization Energy

More on Ionization Energy

The Values of First Ionization Energy for the Elements in the First Six Periods

Successive Ionization Energies (kJ per Mole) for the Elements in Period 3

Electron Affinity

Atomic Radius

Atomic Radii for Selected Atoms

Exercise 3

Exercise 3 - Answer

The Properties of a Group: The Alkali Metals

The Periodic Table - Final Thoughts

Special Names for Groups in the Periodic Table

The Periodic Table - Final Thoughts (cont.)

The Alkali Metals

Chapter 6

Electronic Structure and Periodic Properties of Elements