Chapter 5
Thermochemistry
Shaun Williams, PhD
The Nature of Energy
Energy
- Capacity to do work or to produce heat.
- Law of conservation of energy – energy can be converted from one form to another but can be neither created nor destroyed.
- The total energy content of the universe is constant.
- Potential energy – energy due to position or composition.
- Kinetic energy – energy due to motion of the object and depends on the mass of the object and its velocity.
Ball on a Hill
Initial position - In the initial position, ball A has a higher potential energy than ball B.
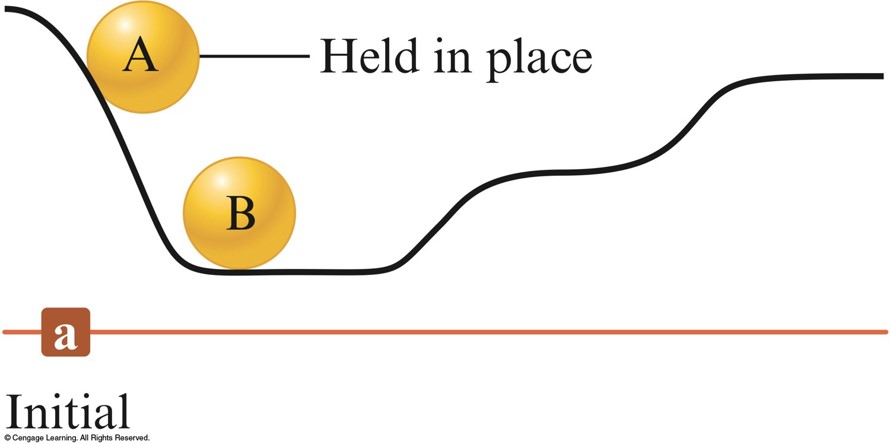
Final position - After A has rolled down the hill, the potential energy lost by A has been converted to random motions of the components of the hill (frictional heating) and to the increase in the potential energy of B.
Energy
- Heat involves the transfer of energy between two objects due to a temperature difference.
- Work – force acting over a distance.
- Energy is a state function; work and heat are not
- State Function – property that does not depend in any way on the system’s past or future (only depends on present state).
Chemical Energy
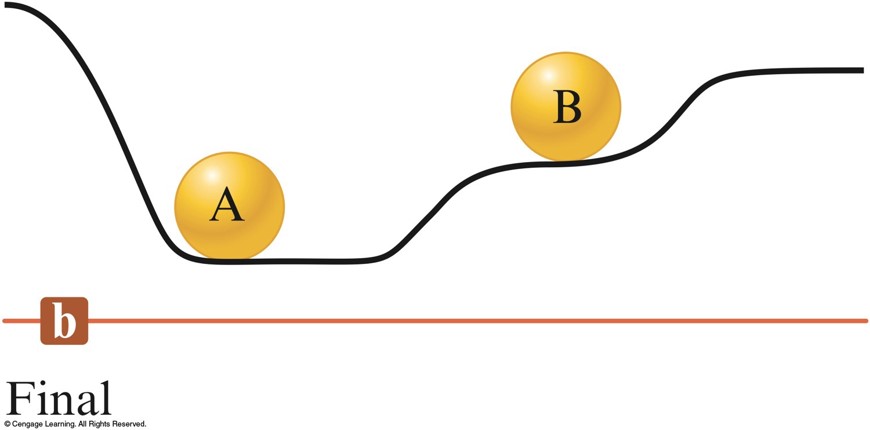
- System – part of the universe on which we wish to focus attention.
- Surroundings – include everything else in the universe.
- Endothermic Reaction:
- Heat flow is into a system.
- Absorb energy from the surroundings.
- Exothermic Reaction:
- Energy flows out of the system.
- Energy gained by the surroundings must be equal to the energy lost by the system.
Thermodynamics
- The study of energy and its interconversions is called thermodynamics.
- Law of conservation of energy is often called the first law of thermodynamics.
Internal Energy
- Internal energy \(E\) of a system is the sum of the kinetic and potential energies of all the "particles" in the system.
- To change the internal energy of a system:
$$ \Delta E = q + w $$
- \(q\) represents heat
- \(w\) represents work
- Thermodynamic quantities consist of two parts:
- Number gives the magnitude of the change.
- Sign indicates the direction of the flow.
The Sign of Internal Energy
- Sign reflects the system’s point of view.
- Endothermic Process:
- \(q\) is positive
- Exothermic Process:
- \(q\) is negative
- System does work on surroundings:
- \(w\) is negative
- Surroundings do work on the system:
- \(w\) is positive
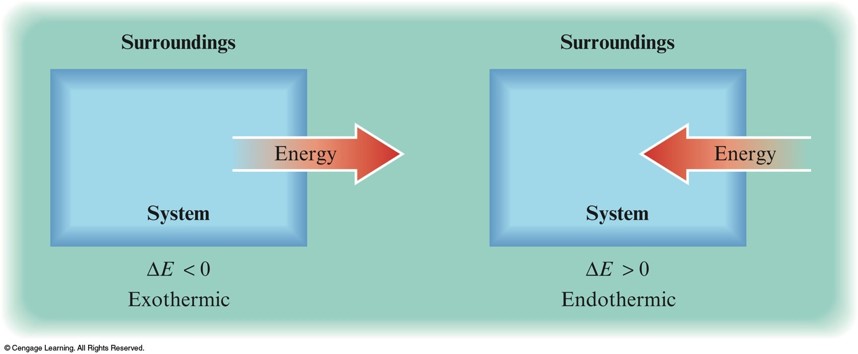
Work
- \(\text{Work} = P × A × \Delta h = P\Delta V\)
- \(P\) is pressure.
- \(A\) is area.
- \(\Delta h\) is the piston moving a distance.
- \(\Delta V\) is the change in volume.
Work - cont.
- For an expanding gas, \(\Delta V\) is a positive quantity because the volume is increasing. Thus \(\Delta V\) and \(w\) must have opposite signs: $$ w=-P\Delta V $$
- To convert between \(\chem{L\cdot atm}\) and \(\chem{Joules}\), use \(1\,\chem{L\cdot atm} = 101.3\,\chem{J}\).
Exercise 1
Which of the following performs more work?
- A gas expanding against a pressure of 2 atm from 1.0 L to 4.0 L.
- A gas expanding against a pressure of 3 atm from 1.0 L to 3.0 L.
Exercise 1 - Answer
Which of the following performs more work?
- A gas expanding against a pressure of 2 atm from 1.0 L to 4.0 L.
- A gas expanding against a pressure of 3 atm from 1.0 L to 3.0 L.
They perform the same amount of work.
Enthalpy and Calorimetry
Change in Enthalpy
- State function
- \(\Delta H = q\) at constant pressure
- \(\Delta H = H_\chem{products} – H_\chem{reactants}\)
Exercise 2
Consider the combustion of propane: $$ \chem{C_3H_8(g) + 5O_2(g) \rightarrow 3CO_2(g) + 4H_2O(l)} \;\;\; \Delta H=-2221\,\chem{kJ}$$ Assume that all of the heat comes from the combustion of propane. Calculate \(\Delta H\) in which 5.00 g of propane is burned in excess oxygen at constant pressure.
Exercise 2 - Answer
Consider the combustion of propane: $$ \chem{C_3H_8(g) + 5O_2(g) \rightarrow 3CO_2(g) + 4H_2O(l)} \;\;\; \Delta H=-2221\,\chem{kJ}$$ Assume that all of the heat comes from the combustion of propane. Calculate \(\Delta H\) in which 5.00 g of propane is burned in excess oxygen at constant pressure.
$$ -252\,\chem{kJ} $$Calorimetry
- Science of measuring heat
- Specific heat capacity:
- The energy required to raise the temperature of one gram of a substance by one degree Celsius.
- Molar heat capacity:
- The energy required to raise the temperature of one mole of substance by one degree Celsius.
- If two reactants at the same temperature are mixed and the resulting solution gets warmer, this means the reaction taking place is exothermic.
- An endothermic reaction cools the solution.
A Coffee-Cup Calorimeter Made if Two Styrofoam Cups
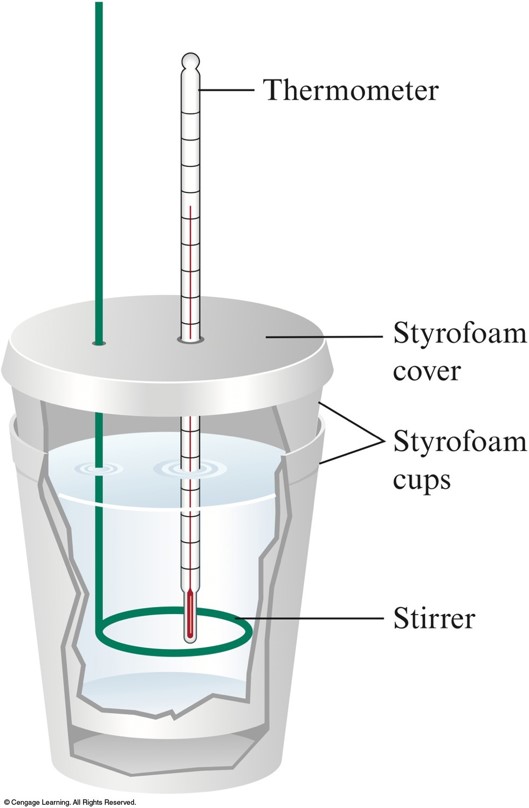
Calorimetry - cont.
- \(\text{Energy released (heat)} = s\times m \times \Delta T\)
- \(s\) - specific heat capacity (\(\bfrac{\chem{J}}{\chem{{}^\circ C\cdot g}}\))
- \(m\) - mass of solution (\(\chem{g}\))
- \(\Delta T\) - change in temperature (\({}^\circ \chem{C}\))
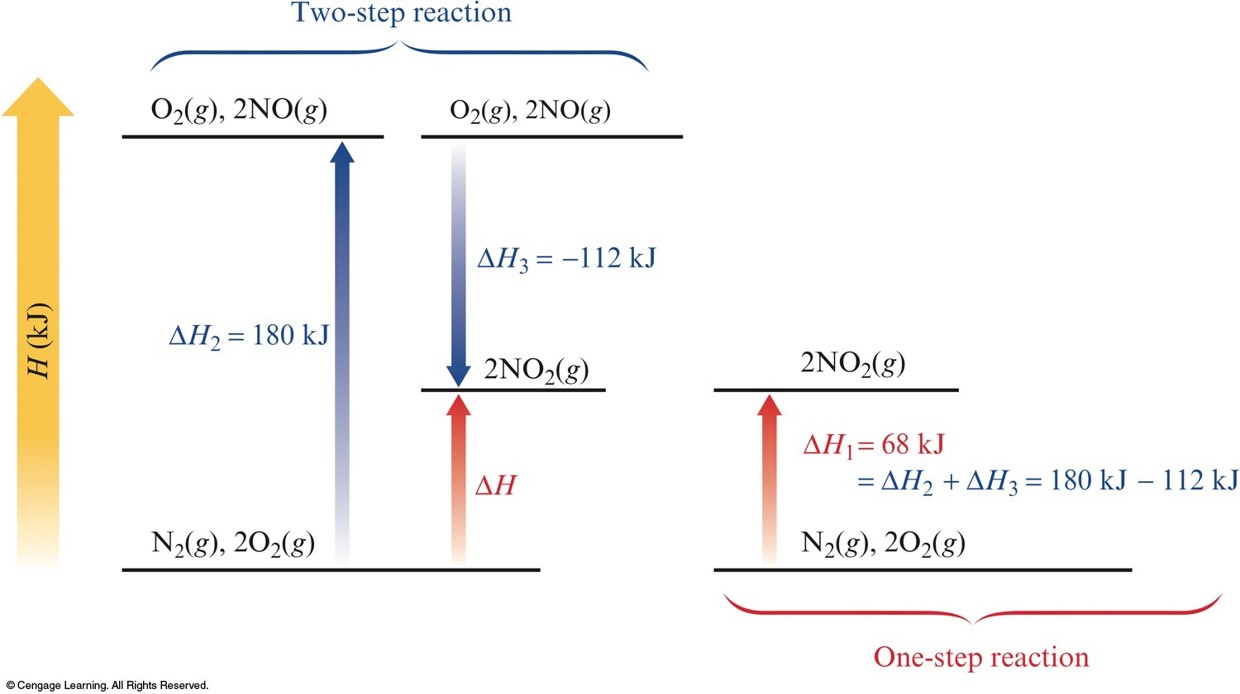
Hess's Law
- In going from a particular set of reactants to a particular set of products, the change in enthalpy is the same whether the reaction takes place in one step or in a series of steps.
\(\chem{N_2(g)+2O_2(g)\rightarrow 2NO_2(g)}\;\;\;\Delta H_1=68\,\chem{kJ}\)
This reaction also can be carried out in two distinct steps, with enthalpy changes designated by \(\Delta H_2\) and \(\Delta H_3\). $$\begin{align} \chem{N_2(g)+O_2(g)} &\rightarrow \chem{\cancel{2NO(g)}} \;\;\;\;\; & \Delta H_2=180\,\chem{kJ} \\ \chem{\cancel{2NO(g)}+O_2(g)} &\rightarrow \chem{2NO_2(g)} \;\;\;\;\; & \Delta H_3=-112\,\chem{kJ} \\ \hline \chem{N_2(g)+2O_2(g)} &\rightarrow \chem{2NO_2(g)} \;\;\;\;\; & \Delta H_2+\Delta H_3=68\,\chem{kJ} \end{align}$$ So we see that $$ \Delta H_1 = \Delta H_2+\Delta H_3 = 68\,\chem{kJ} $$
The Principle of Hess's Law
Characteristics of Enthalpy Changes
- If a reaction is reversed, the sign of \(\Delta H\) is also reversed.
- The magnitude of \(\Delta H\) is directly proportional to the quantities of reactants and products in a reaction. If the coefficients in a balanced reaction are multiplied by an integer, the value of \(\Delta H\) is multiplied by the same integer.
Example
Consider the following data: $$\begin{align} \chem{NH_3(g)} &\rightarrow \chem{\frac{1}{2}N_2(g)+\frac{3}{2}H_2(g)} \;\;\; &\Delta H=46\,\chem{kJ} \\ \chem{2H_2(g)+O_2(g)} &\rightarrow \chem{2H_2O(g)} \;\;\; &\Delta H=-484\,\chem{kJ} \end{align}$$ Calculate \(\Delta H\) for the reaction $$ \chem{2N_2(g)+6H_2O(g)\rightarrow 3O_2(g)+4NH_3(g)} $$
Problem-Solving Strategy
- Work backward from the required reaction, using the reactants and products to decide how to manipulate the other given reactions at your disposal.
- Reverse any reactions as needed to give the required reactants and products.
- Multiply reactions to give the correct numbers of reactants and products.
Standard Enthalpies of Formation
Standard Enthalpies of Formation \(\left(\Delta H^\circ_f\right)\)
- Change in enthalpy that accompanies the formation of one mole of a compound from its elements with all substances in their standard states.
Conventional Definitions of Standard States
- For a Compound
- For a gas, pressure is exactly 1 atm.
- For a solution, concentration is exactly 1 M.
- Pure substance (liquid or solid)
- For an Element - The form [\(\chem{N_2(g)}\), \(\chem{K(s)}\)] in which it exists at 1 atm and 25°C.
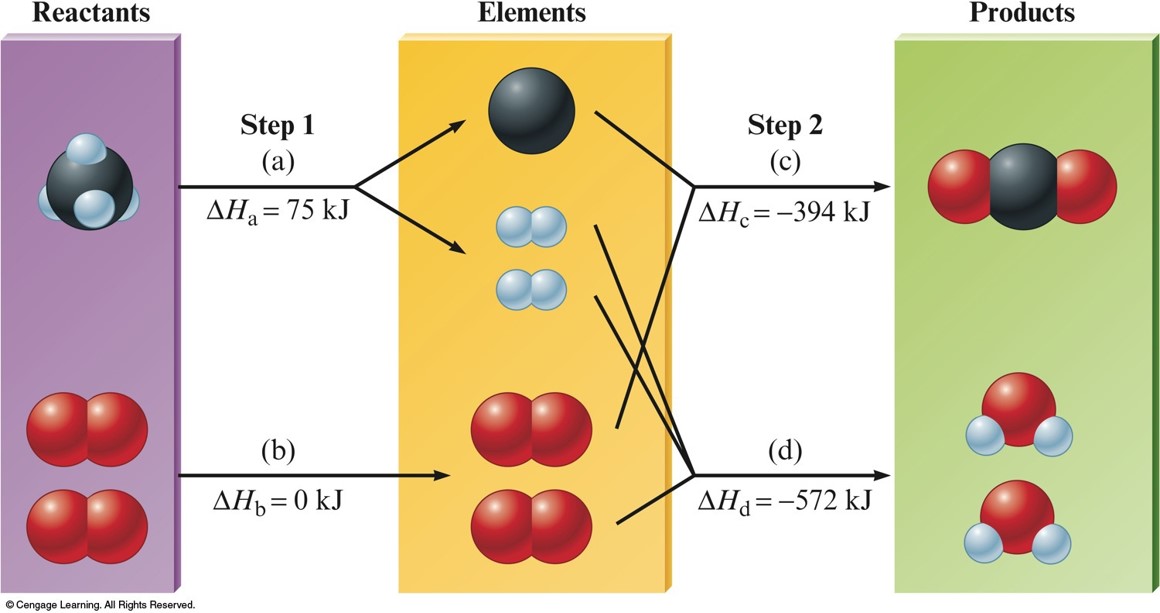
A Schematic Diagram of the Energy Changes for the Reaction $$\chem{CH_4(g) + 2O_2(g) \rightarrow CO_2(g) + 2H_2O(l)}$$
$$ \Delta H^\circ_\chem{reaction} = -\left(-75\,\chem{kJ}\right) + 0 + \left(-394\,\chem{kJ}\right) + \left(-572\,\chem{kJ}\right) = -891\,\chem{kJ} $$
Problem-Solving Strategy: Enthalpy Calculations
- When a reaction is reversed, the magnitude of \(\Delta H\) remains the same, but its sign changes.
- When the balanced equation for a reaction is multiplied by an integer, the value of \(\Delta H\) for that reaction must be multiplied by the same integer.
- The change in enthalpy for a given reaction can be calculated from the enthalpies of formation of the reactants and products: $$ \Delta H^\circ_\chem{rxn} = \sum n_\chem{p} \Delta H^\circ_f\left(\chem{products}\right) - \sum n_\chem{r} \Delta H^\circ_f\left(\chem{reactants}\right) $$
- Elements in their standard states are not included in the \(\Delta H_\chem{reaction}\) calculations because \(\Delta H^\circ_f\) for an element in its standard state is zero.
Excercise 3
Calculate \(\Delta H^\circ\) for the following reaction: $$ \chem{2Na(s) + 2H_2O(l) \rightarrow 2NaOH(aq) + H_2(g)} $$ Given the following information:
| \(\Delta H^\circ_f\,\left(\bfrac{\chem{kJ}}{\chem{mol}}\right)\) | |
|---|---|
| \(\chem{Na(s)}\) | 0 |
| \(\chem{H_2O(l)}\) | -286. |
| \(\chem{NaOH(aq)}\) | -470. |
| \(\chem{H_2(g)}\) | 0 |
Excercise 3 - Answer
Calculate \(\Delta H^\circ\) for the following reaction: $$ \chem{2Na(s) + 2H_2O(l) \rightarrow 2NaOH(aq) + H_2(g)} $$ Given the following information:
| \(\Delta H^\circ_f\,\left(\bfrac{\chem{kJ}}{\chem{mol}}\right)\) | |
|---|---|
| \(\chem{Na(s)}\) | 0 |
| \(\chem{H_2O(l)}\) | -286. |
| \(\chem{NaOH(aq)}\) | -470. |
| \(\chem{H_2(g)}\) | 0 |
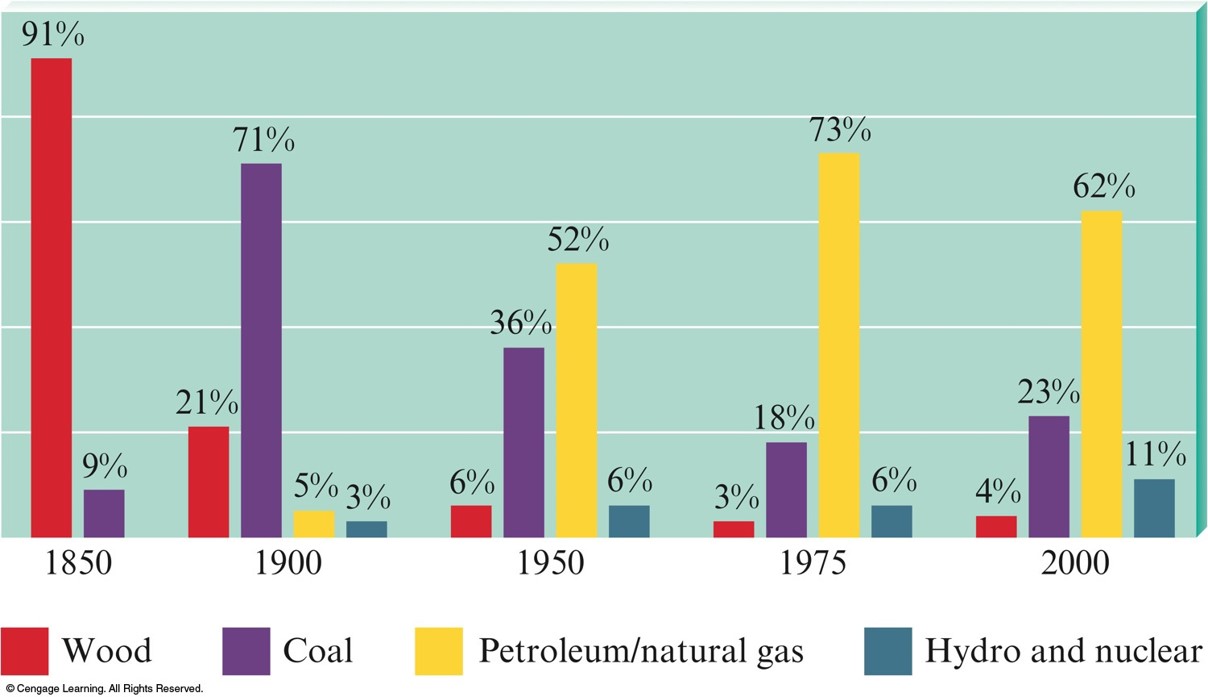
Present Sources of Energy
- Fossil Fuels
- Petroleum, Natural Gas, and Coal
- Wood
- Hydro
- Nuclear
Energy Sources Used in the United States
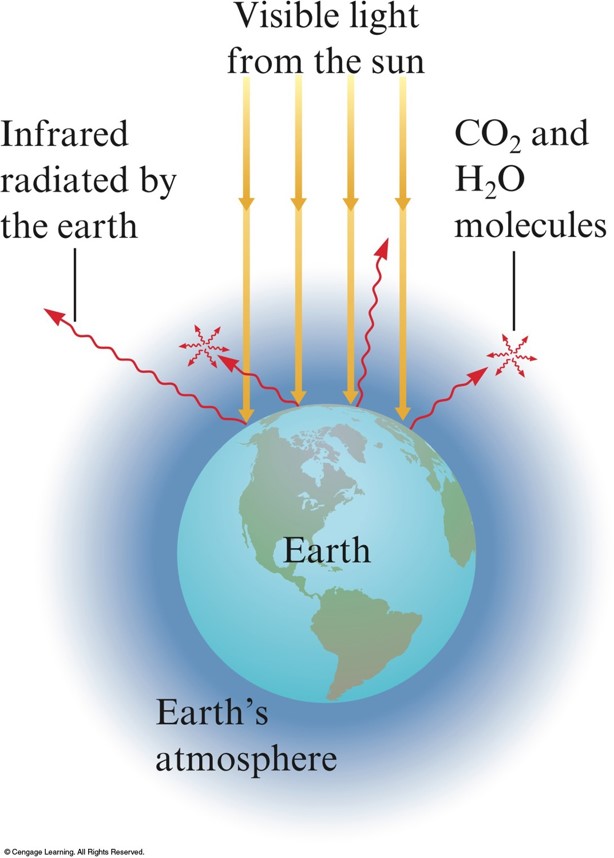
The Earth's Atmosphere
- Transparent to visible light from the sun.
- Visible light strikes the Earth, and part of it is changed to infrared radiation.
- Infrared radiation from Earth’s surface is strongly absorbed by \(\chem{CO_2}\), \(\chem{H_2O}\), and other molecules present in smaller amounts in atmosphere.
- Atmosphere traps some of the energy and keeps the Earth warmer than it would otherwise be.
New Energy Sources
- Coal Conversion
- Hydrogen as a Fuel
- Other Energy Alternatives
- Oil shale
- Ethanol
- Methanol
- Seed oil
/