Chapter 3

Stoichiometry

Shaun Williams, PhD

Chemical Stoichiometry

• Stoichiometry – The study of quantities of materials consumed and produced in chemical reactions.

Counting by Weighing

• Objects behave as though they were all identical.
• Atoms are too small to count.
• Need average mass of the object.

Exercise 1

A pile of marbles weigh 394.80 g. 10 marbles weigh 37.60 g. How many marbles are in the pile?

Exercise 1 - Answer

A pile of marbles weigh 394.80 g. 10 marbles weigh 37.60 g. How many marbles are in the pile?

Atomic Masses

• \({}^{12}\chem{C}\) is the standard for atomic mass, with a mass of exactly 12 atomic mass units (u).
• The masses of all other atoms are given relative to this standard.
• Elements occur in nature as mixtures of isotopes.
• Carbon =
  • \(98.89\%\, {}^{12}\chem{C}\)
  • \(1.11\%\, {}^{13}\chem{C}\)
  • \(\lt 0.01\%\, {}^{14}\chem{C}\)

Average Atomic Mass for Carbon

• Even though natural carbon does not contain a single atom with mass 12.01, for stoichiometric purposes, we can consider carbon to be composed of only one type of atom with a mass of 12.01.
• This enables us to count atoms of natural carbon by weighing a sample of carbon.

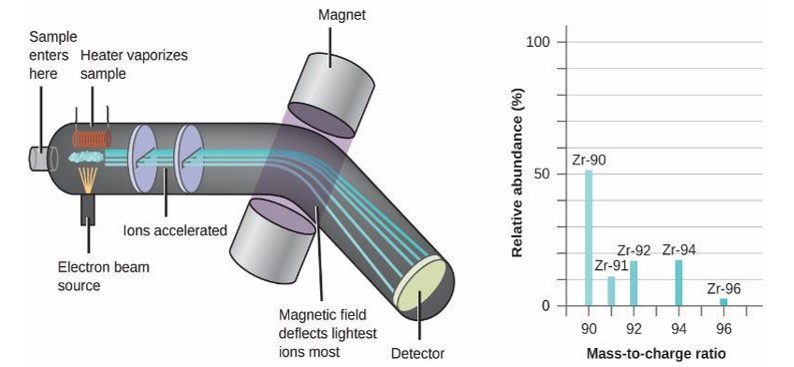
Exercise 2

An element consists of 62.60% of an isotope with mass 186.956 u and 37.40% of an isotope with mass 184.953 u.

Calculate the average atomic mass and identify the element

Exercise 2 - Answer

An element consists of 62.60% of an isotope with mass 186.956 u and 37.40% of an isotope with mass 184.953 u.

Calculate the average atomic mass and identify the element

The Mole

• The number equal to the number of carbon atoms in exactly 12 grams of pure \({}^{12}\chem{C}\).
• 1 mole of something consists of \(6.022 \times 10^{23}\,\chem{units}\) of that substance (Avogadro’s number).
• \(1\,\text{mole C} = 6.022 \times 10^{23}\,\text{C atoms} = 12.01\,\chem{g\,C}\)

Exercise 3

Calculate the number of iron atoms in a 4.48 mole sample of iron.

Exercise 3 - Answer

Calculate the number of iron atoms in a 4.48 mole sample of iron.

Molar Mass

• Mass in grams of one mole of the substance:
  • Molar Mass of \(\chem{N} = 14.01\,\bfrac{\chem{g}}{\chem{mol}}\)
  • Molar Mass of \(\chem{H_2O} = 18.02\,\bfrac{\chem{g}}{\chem{mol}}\) $$ \left(2 × 1.008\,\bfrac{\chem{g}}{\chem{mol}}\right) + 16.00\,\bfrac{\chem{g}}{\chem{mol}} $$
  • Molar Mass of \(\chem{Ba(NO_3)_2} = 261.35\,\bfrac{\chem{g}}{\chem{mol}}\) $$ 137.33\,\bfrac{\chem{g}}{\chem{mol}} + \left(2 × 14.01\,\bfrac{\chem{g}}{\chem{mol}}\right) + \left(6 × 16.00\,\bfrac{\chem{g}}{\chem{mol}}\right) $$

Concept Check!

Calculate the number of copper atoms in a 63.55 g sample of copper.

Concept Check! - Answer

Calculate the number of copper atoms in a 63.55 g sample of copper.

Percent Composition of Compounds

• Mass percent of an element: $$ \text{mass %} = \frac{\text{mass of element in compound}}{\text{mass of compound}} \times 100\% $$
• For iron in iron(III) oxide, (\(\chem{Fe_2O_3}\)): $$ \begin{align} \text{mass % Fe} &= \frac{2(55.85\,\chem{g})}{2(55.85\,\chem{g})+3(16.00\,\chem{g})} \times 100\% \\ &= \frac{111.70\,\chem{g}}{159.70\,\chem{g}} \times 100\% = 69.94\% \end{align} $$

Determining the Formula of a Compound

Formulas

• Empirical formula = \(\chem{CH}\)
  • Simplest whole-number ratio
• Molecular formula = \((\text{empirical formula})_n\) where \(n\) is an integer
• Molecular formula = \(\chem{C_6H_6} = (\chem{CH})_6\)
  • Actual formula of the compound

Analyzing for Carbon and Hydrogen

• Device used to determine the mass percent of each element in a compound.

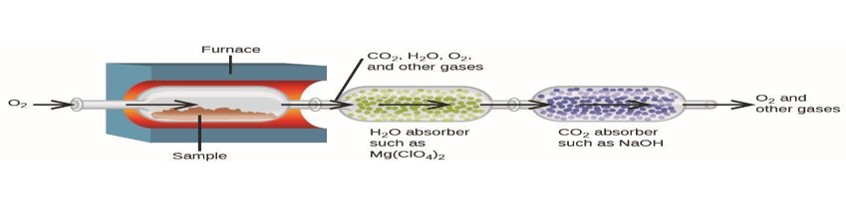
Exercise 4

The composition of adipic acid is 49.3% C, 6.9% H, and 43.8% O (by mass). The molar mass of the compound is about \(146\,\bfrac{\chem{g}}{\chem{mol}}\).

• What is the empirical formula? $$ \phantom{C} $$
• What is the molecular formula? $$ \phantom{C} $$

Exercise 4 - Answer

The composition of adipic acid is 49.3% C, 6.9% H, and 43.8% O (by mass). The molar mass of the compound is about \(146\,\bfrac{\chem{g}}{\chem{mol}}\).

• What is the empirical formula? $$ \chem{C_3H_5O_2} $$
• What is the molecular formula? $$ \chem{C_6H_{10}O_4} $$

Chemical Equations

$$ \chem{C_2H_5OH + 3O_2 \rightarrow 2CO_2 + 3H_2O} $$

• The equation is balanced.
• All atoms present in the reactants are accounted for in the products.
• 1 mole of ethanol reacts with 3 moles of oxygen to produce 2 moles of carbon dioxide and 3 moles of water.
• The balanced equation represents an overall ratio of reactants and products, not what actually “happens” during a reaction.
• Use the coefficients in the balanced equation to decide the amount of each reactant that is used, and the amount of each product that is formed.

Balancing Chemical Equations

Writing and Balancing the Equation for a Chemical Reaction

1. Determine what reaction is occurring. What are the reactants, the products, and the physical states involved?
2. Write the unbalanced equation that summarizes the reaction described in step 1.
3. Balance the equation by inspection, starting with the most complicated molecule(s). The same number of each type of atom needs to appear on both reactant and product sides. Do NOT change the formulas of any of the reactants or products.

Notice

• The number of atoms of each type of element must be the same on both sides of a balanced equation.
• Subscripts must not be changed to balance an equation.
• A balanced equation tells us the ratio of the number of molecules which react and are produced in a chemical reaction.
• Coefficients can be fractions, although they are usually given as lowest integer multiples.

Stoichiometric Calculations Amounts of Reactants and Products

• Chemical equations can be used to relate the masses of reacting chemicals.

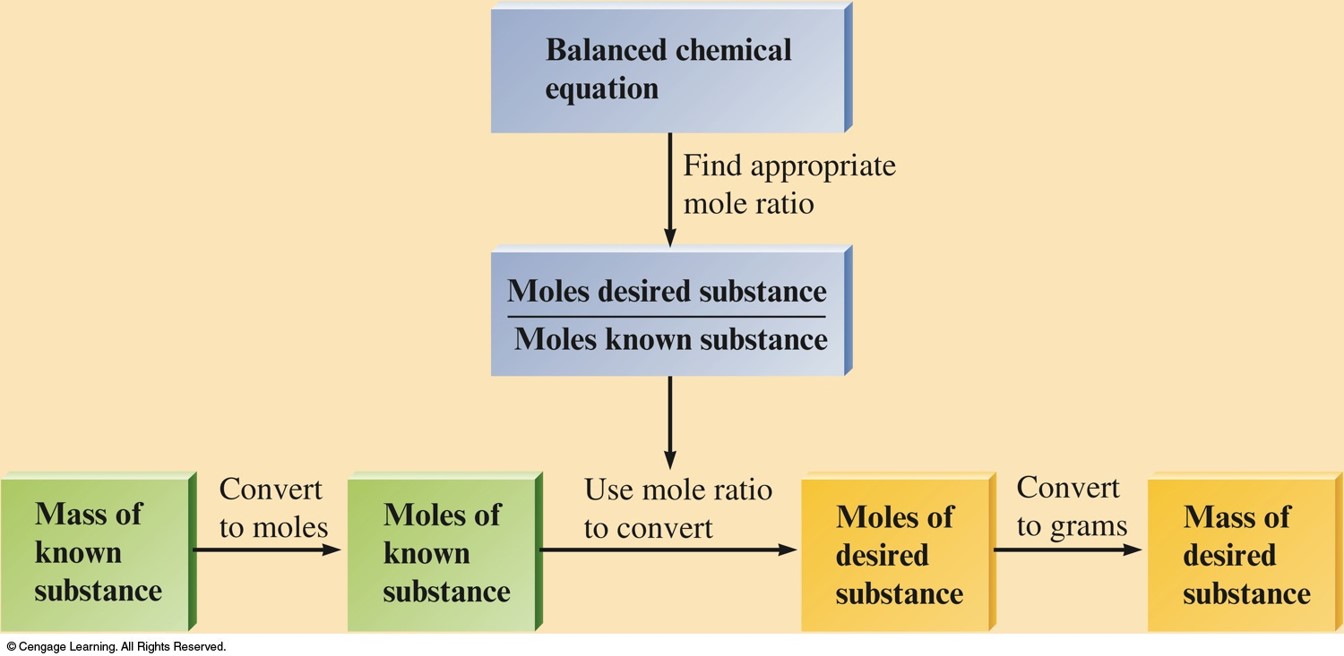
Calculating Masses of Reactants and Products in Reactions

1. Balance the equation for the reaction.
2. Convert the known mass of the reactant or product to moles of that substance.
3. Use the balanced equation to set up the appropriate mole ratios.
4. Use the appropriate mole ratios to calculate the number of moles of the desired reactant or product.
5. Convert from moles back to grams if required by the problem.

Calculating Masses of Reactants and Products - Graphically

Exercise 4

Consider the following reaction: $$ \chem{P_4(s)+5O_2(g) \rightarrow 2P_2O_5(s)} $$ If 6.25 g of phosphorus is burned, what mass of oxygen does it combine with?

Exercise 4 - Answer

Consider the following reaction: $$ \chem{P_4(s)+5O_2(g) \rightarrow 2P_2O_5(s)} $$ If 6.25 g of phosphorus is burned, what mass of oxygen does it combine with?

Limiting Reactants

• Limiting reactant - the reactant that runs out first and thus limits the amounts of products that can be formed.
• Determine which reactant is limiting to calculate correctly the amounts of products that will be formed.

A. The Concept of Limiting Reactants

Stoichiometric mixture $$ \chem{N_2(g)+3H_2(g) \rightarrow 2NH_3(g)} $$

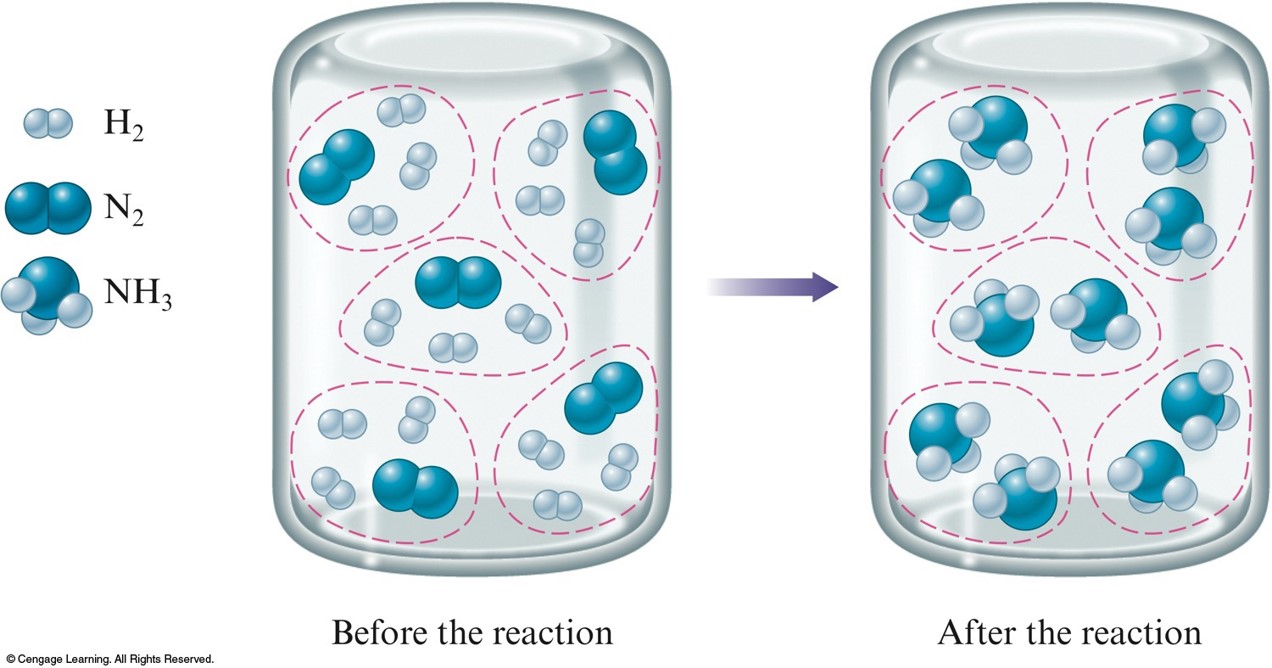
A. The Concept of Limiting Reactants

Limiting reactant mixture $$ \chem{N_2(g)+3H_2(g) \rightarrow 2NH_3(g)} $$

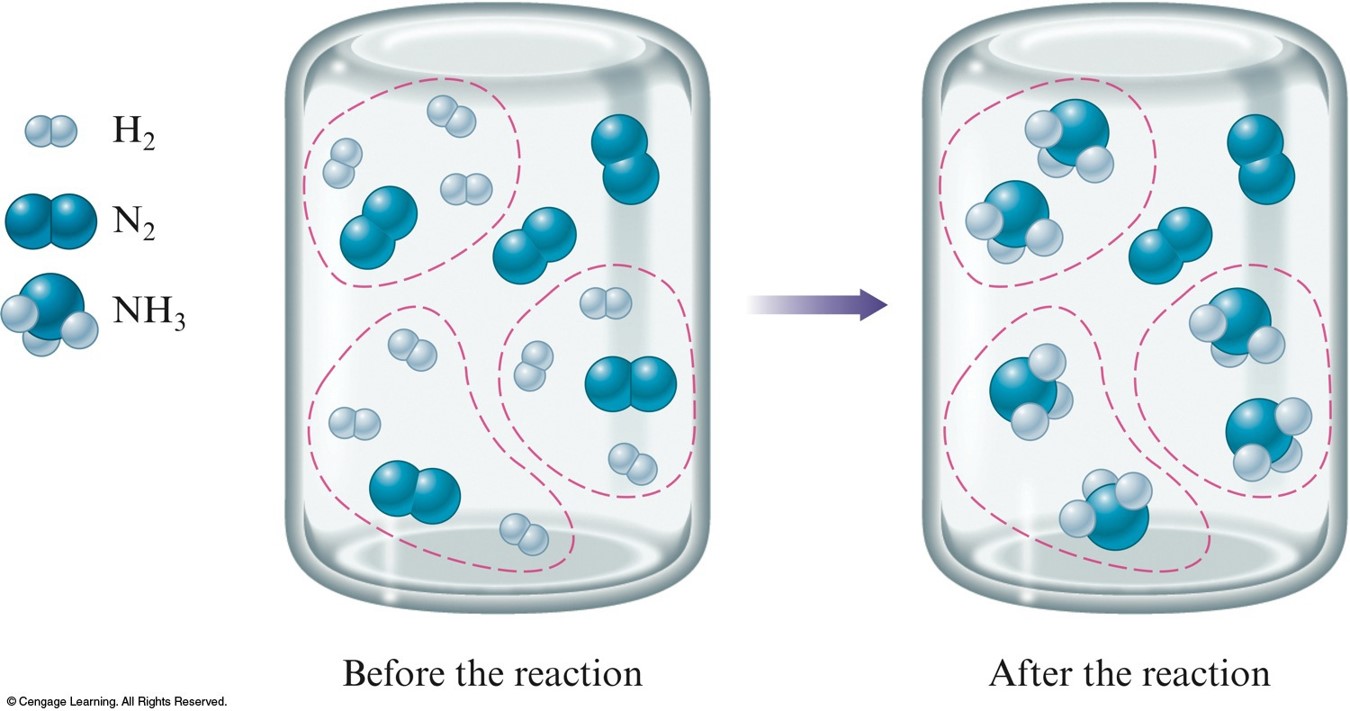
• Limiting reactant is the reactant that runs out first.
  • \( \chem{H_2} \)

Notice

• We cannot simply add the total moles of all the reactants to decide which reactant mixture makes the most product. We must always think about how much product can be formed by using what we are given, and the ratio in the balanced equation.

Percent Yield

• An important indicator of the efficiency of a particular laboratory or industrial reaction. $$ \frac{\text{Actual yield}}{\text{Theoretical yield}} \times 100\% = \text{Percent yield} $$

Exercise 6

Consider the following reaction: $$ \chem{P_4(s)+6F_2(g) \rightarrow 4PF_3(g)} $$ What mass of \(\chem{P_4}\) is needed to produce 85.0 g of \(\chem{PF_3}\) if the reaction has a 64.9% yield?

Exercise 6 - Answer

Consider the following reaction: $$ \chem{P_4(s)+6F_2(g) \rightarrow 4PF_3(g)} $$ What mass of \(\chem{P_4}\) is needed to produce 85.0 g of \(\chem{PF_3}\) if the reaction has a 64.9% yield?

$$ 46.1\,\chem{g}\,\chem{P_4} $$