Chapter 17

Electrochemistry

Shaun Williams, PhD

Review of Terms

Electrochemistry – the study of the interchange of chemical and electrical energy
Oxidation–reduction (redox) reaction – involves a transfer of electrons from the reducing agent to the oxidizing agent
Oxidation – loss of electrons
Reduction – gain of electrons
Reducing agent – electron donor
Oxidizing agent – electron acceptor

Half-Reactions

The overall reaction is split into two half–reactions, one involving oxidation and one involving reduction. $$ \begin{align} &\chem{8H^+ + MnO_4^- + 5Fe^{2+} \rightarrow Mn^{2+} + 5Fe^{3+} + 4H_2O} \\ &\text{Reduction: }\chem{8H^+ + MnO_4^- + 5e^- \rightarrow Mn^{2+} + 4H_2O} \\ &\text{Oxidation: }\chem{5Fe^{2+} \rightarrow 5Fe^{3+} + 5e^-} \end{align} $$

The Half–Reaction Method for Balancing Equations for Oxidation–Reduction Reactions Occurring in Acidic Solution

Write separate equations for the oxidation and reduction half–reactions.
For each half–reaction:

Balance all the elements except $\chem{H}$ and $\chem{O}$.
Balance $\chem{O}$ using $\chem{H_2O}$.
Balance $\chem{H}$ using $\chem{H^+}$.
Balance the charge using electrons.

If necessary, multiply one or both balanced half–reactions by an integer to equalize the number of electrons transferred in the two half–reactions.
Add the half–reactions, and cancel identical species.
Check that the elements and charges are balanced.

Example

$\chem{Cr_2O_7^{2-}(aq) + SO_3^{2-}(aq) \rightarrow Cr^{3+}(aq) + SO_4^{2-}(aq)}$

Seperate this into half-reactions $$ \begin{align} \chem{Cr_2O_7^{2-}(aq)} &\rightarrow \chem{Cr^{3+}(aq)} \\ \chem{SO_3^{2-}(aq)} &\rightarrow \chem{SO_4^{2-}(aq)} \end{align}$$
Balance all the elements except $\chem{H}$ and $\chem{O}$ $$ \begin{align} \chem{Cr_2O_7^{2-}(aq)} &\rightarrow \chem{2Cr^{3+}(aq)} \\ \chem{SO_3^{2-}(aq)} &\rightarrow \chem{SO_4^{2-}(aq)} \end{align}$$

Example Continued

$$ \begin{align} \chem{Cr_2O_7^{2-}(aq)} &\rightarrow \chem{2Cr^{3+}(aq)} \\ \chem{SO_3^{2-}(aq)} &\rightarrow \chem{SO_4^{2-}(aq)} \end{align}$$

Add electrons based on changes in oxidation states $$ \begin{align} \chem{6e^- + Cr_2O_7^{2-}(aq)} &\rightarrow \chem{Cr^{3+}(aq)} \\ \chem{SO_3^{2-}(aq)} &\rightarrow \chem{SO_4^{2-}(aq) + 2e^-} \end{align}$$
Balance the oxygen atoms using $\chem{H_2O}$ $$ \begin{align} \chem{6e^- + Cr_2O_7^{2-}(aq)} &\rightarrow \chem{2Cr^{3+}(aq) + 7H_2O} \\ \chem{H_2O + SO_3^{2-}(aq)} &\rightarrow \chem{SO_4^{2-}(aq) + 2e^-} \end{align}$$

Example Continued Further

$$ \begin{align} \chem{6e^- + Cr_2O_7^{2-}(aq)} &\rightarrow \chem{2Cr^{3+}(aq) + 7H_2O} \\ \chem{H_2O + SO_3^{2-}(aq)} &\rightarrow \chem{SO_4^{2-}(aq) + 2e^-} \end{align}$$

Balance the hydrogen atoms using $\chem{H^+}$ $$ \begin{align} \chem{14H^+ + 6e^- + Cr_2O_7^{2-}(aq)} &\rightarrow \chem{2Cr^{3+}(aq) + 7H_2O} \\ \chem{H_2O + SO_3^{2-}(aq)} &\rightarrow \chem{SO_4^{2-}(aq) + 2e^- + 2H^+} \end{align}$$
Balance the electrons between the half-reactions $$ \begin{align} \chem{14H^+ + 6e^- + Cr_2O_7^{2-}(aq)} &\rightarrow \chem{2Cr^{3+}(aq) + 7H_2O} \\ 3\left[\chem{H_2O + SO_3^{2-}(aq)}\right. &\rightarrow \left.\chem{SO_4^{2-}(aq) + 2e^- + 2H^+}\right] \end{align}$$

Example Concluded

$$ \begin{align} \chem{14H^+ + 6e^- + Cr_2O_7^{2-}(aq)} &\rightarrow \chem{2Cr^{3+}(aq) + 7H_2O} \\ 3\left[\chem{H_2O + SO_3^{2-}(aq)}\right. &\rightarrow \left.\chem{SO_4^{2-}(aq) + 2e^- + 2H^+}\right] \end{align}$$

Distributing $$ \begin{align} \chem{14H^+ + 6e^- + Cr_2O_7^{2-}(aq)} &\rightarrow \chem{2Cr^{3+}(aq) + 7H_2O} \\ 3\chem{H_2O + 3SO_3^{2-}(aq)} &\rightarrow \chem{3SO_4^{2-}(aq) + 6e^- + 6H^+} \end{align}$$
Add the reactions together cancel out species on each side of the reaction to get the final balance equation $$ \chem{Cr_2O_7^{2-} + 3SO_3^{2-} + 8H^+ \rightarrow 2Cr^{3+} + 3SO_4^{2-} + 4H_2O} $$

Exercise

Balance the following oxidation-reduction reaction that occurs in acidic solution $$ \chem{Br^-(aq) + MnO_4^-(aq) \rightarrow Br_2(l) + Mn^{2+}(aq)} $$

$$ \begin{align} \chem{10Br^-(aq)} + \chem{16H^+(aq)} + \chem{2MnO_4^-(aq)} \rightarrow \\ \chem{5Br_2(l)} + \chem{2Mn^{2+}(aq)} + \chem{8H_2O(l)} \end{align} $$

The Half–Reaction Method for Balancing Equations for Oxidation–Reduction Reactions Occurring in Basic Solution

Use the half–reaction method as specified for acidic solutions to obtain the final balanced equation as if $\chem{H^+}$ ions were present.
To both sides of the equation obtained above, add a number of $\chem{OH^–}$ ions that is equal to the number of $\chem{H^+}$ ions. (We want to eliminate $\chem{H^+}$ by forming $\chem{H_2O}$.)
Form $\chem{H_2O}$ on the side containing both $\chem{H^+}$ and $\chem{OH^–}$ ions, and eliminate the number of H2O molecules that appear on both sides of the equation.
Check that elements and charges are balanced.

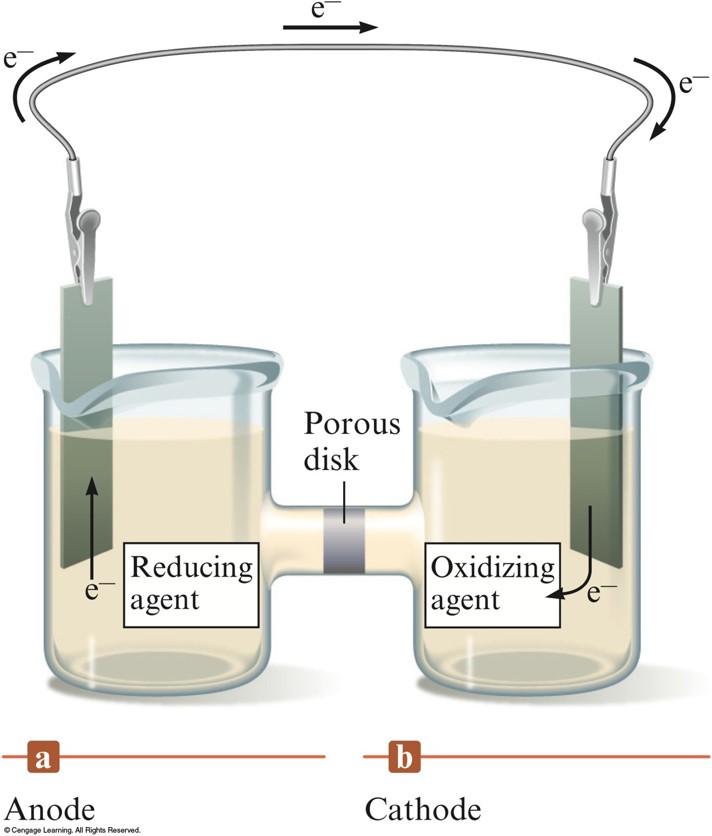
Galvantic Cell

Device in which chemical energy is changed to electrical energy.
Uses a spontaneous redox reaction to produce a current that can be used to do work.
Oxidation occurs at the anode.
Reduction occurs at the cathode.
Salt bridge or porous disk – devices that allow ions to flow without extensive mixing of the solutions.

Salt bridge – contains a strong electrolyte held in a Jello–like matrix.
Porous disk – contains tiny passages that allow hindered flow of ions.

The Galvantic Cell

Oxidation is occuring at the anode in the presence of the reducing agent. Reduction is occuring at the cathode in the presence of the oxidizing agent. A wire connects the anode and cathode. Additionally the two chambers of the galvanic cell as connected through a porous disk.

Cell Potential

A galvanic cell consists of an oxidizing agent in one compartment that pulls electrons through a wire from a reducing agent in the other compartment.
The “pull”, or driving force, on the electrons is called the cell potential ($\mathcal{E}_{cell}$), or the electromotive force (emf) of the cell.

Unit of electrical potential is the volt (V).

1 joule of work per coulomb of charge transferred.

More on Galvanic Cells

All half-reactions are given as reduction processes in standard tables.

Table 18.1
$1\,\mathrm{M}$, $1\,\mathrm{atm}$, $25^\circ\mathrm{C}$

When a half-reaction is reversed, the sign of $E^\circ$ is reversed.
When a half-reaction is multiplied by an integer, $E^\circ$ remains the same.
A galvanic cell runs spontaneously in the direction that gives a positive value for $E^\circ_{cell}$.

Example: $\chem{Fe^{3+}(aq) + Cu(s) → Cu^{2+}(aq) + Fe^{2+}(aq)}$

Half-Reactions: $$ \begin{align} &\chem{Fe^{3+}+e^- \rightarrow Fe^{2+}} & E^\circ = 0.77\,\mathrm{V} \\ &\chem{Cu^{2+}+2e^- \rightarrow Cu} & E^\circ = 0.34\,\mathrm{V} \\ \end{align} $$
To balance the cell reaction and calculate the cell potential, we must reverse reaction 2. $$ \chem{Cu \rightarrow Cu^{2+} + 2e^-} \;\;\;\; E^\circ = -0.34\,\mathrm{V} $$
Each $\chem{Cu}$ atom produces two electrons but each $\chem{Fe^{3+}}$ ion accepts only one electron, therefore reaction 1 must be multiplied by 2. $$ \chem{2Fe^{3+} + 2e^- \rightarrow 2Fe^{2+}} \;\;\;\; E^\circ = 0.77\,\mathrm{V} $$

Overall Balanced Cell Reaction

$$ \begin{align} &\chem{2Fe^{3+}+2e^- \rightarrow 2Fe^{2+}} & E^\circ = 0.77\,\mathrm{V} \\ &\chem{Cu \rightarrow Cu^{2+}+2e^-} & E^\circ = -0.34\,\mathrm{V} \\ \end{align} $$

Balanced Cell Reaction: $$ \chem{Cu + 2Fe^{3+} \rightarrow Cu^{2+} + 2Fe^{2+}} $$
Cell Potential: $$ \begin{align} E^\circ_{cell} &= E^\circ (\mathrm{cathode}) - E^\circ (\mathrm{anode}) \\ E^\circ_{cell} &= 0.77\,\mathrm{V} - 0.34\,\mathrm{V} = 0.43\,\mathrm{V} \end{align} $$

Line Notation

Used to describe electrochemical cells.
Anode components are listed on the left.
Cathode components are listed on the right.
Separated by double vertical lines which indicated salt bridge or porous disk.
The concentration of aqueous solutions should be specified in the notation when known.
Example: $ \chem{Mg(s) | Mg^{2+}(aq) || Al^{3+}(aq) | Al(s)} $

$ \chem{Mg \rightarrow Mg^{2+} + 2e^-}\;\;\;\mathrm{(anode)} $
$ \chem{Al^{3+} + 3e^- \rightarrow Al}\;\;\;\;\;\mathrm{(cathode)} $

Description of a Galvanic Cell

The cell potential (always positive for a galvanic cell where $E^\circ_{cell} = E^\circ (\mathrm{cathode}) – E^\circ (\mathrm{anode})$ and the balanced cell reaction.
The direction of electron flow, obtained by inspecting the half–reactions and using the direction that gives a positive $E^\circ_{cell}$.
Designation of the anode and cathode.
The nature of each electrode and the ions present in each compartment. A chemically inert conductor is required if none of the substances participating in the half–reaction is a conducting solid.

Work

Work is never the maximum possible if any current is flowing.
In any real, spontaneous process some energy is always wasted – the actual work realized is always less than the calculated maximum.

Maximum Cell Potential

Directly related to the free energy difference between the reactants and the products in the cell.

$ \Delta G^\circ = –nFE^\circ $

$ F = 96485\,\bfrac{\mathrm{C}}{\mathrm{mol\cdot e^-}} $

A Concentration Cell

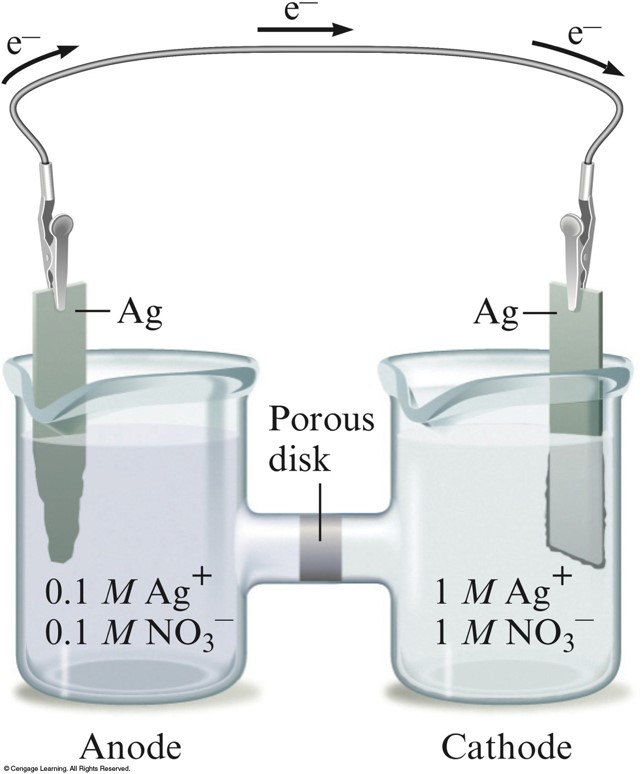
$A galvanic cell in which both solutions and both metals are the same. The anode cell contains a $0.1\,\mathrm{M}$ solution while the cathode cell contains a $1.0\,\mathrm{M}$ solution.$

Nernst Equation

The relationship between cell potential and concentrations of cell components
At $25^\circ\mathrm{C}$: $$ \begin{align} \mathcal{E} &= \mathcal{E}^\circ - \frac{0.0591}{n} \log (Q) \\ &\mathrm{or} \\ \mathcal{E}^\circ &= \frac{0.0591}{n}\log (K) \;\;\; \text{(at equilibrium)} \end{align} $$

Exercise

A concentration cell is constructed using two nickel electrodes with $\chem{Ni^{2+}}$ concentrations of $1.0\,\mathrm{M}$ and $1.00 \times 10^{-4}\,\mathrm{M}$ in the two half-cells.

Calculate the potential of this cell at $25^\circ\mathrm{C}$.

$0.118\,\mathrm{V}$

Concept Check

You make a galvanic cell at $25^\circ\mathrm{C}$ containing:

A nickel electrode in $ 1.0\,\mathrm{M}\,\chem{Ni^{2+}(aq)} $
A silver electrode in $ 1.0\,\mathrm{M}\,\chem{Ag^+(aq)} $

Sketch this cell, labeling the anode and cathode, showing the direction of the electron flow, and calculate the cell potential.

$ 1.03\,\mathrm{V} $

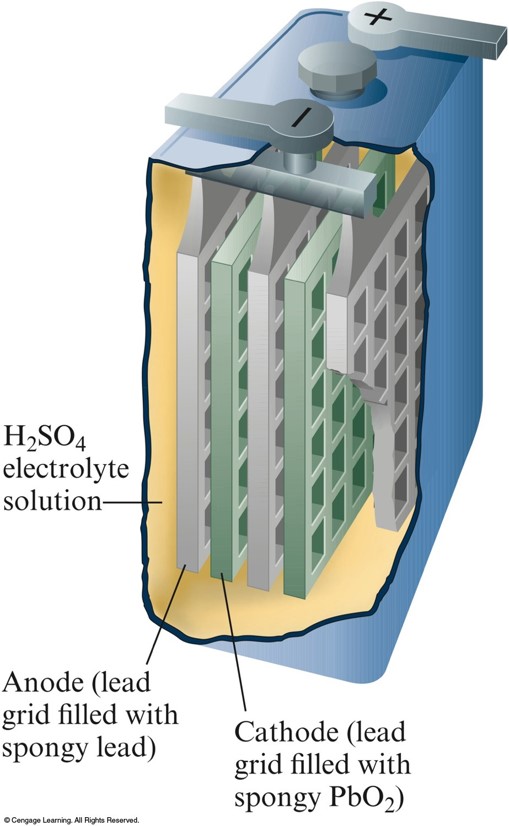
One of the Six Cells in a 12–V Lead Storage Battery

A diagram of a lead acid battery showing alternating plates of anodes (made of lead) and cathodes (made of lead(IV) oxide). The plates are in a solution of sulfuric acid.

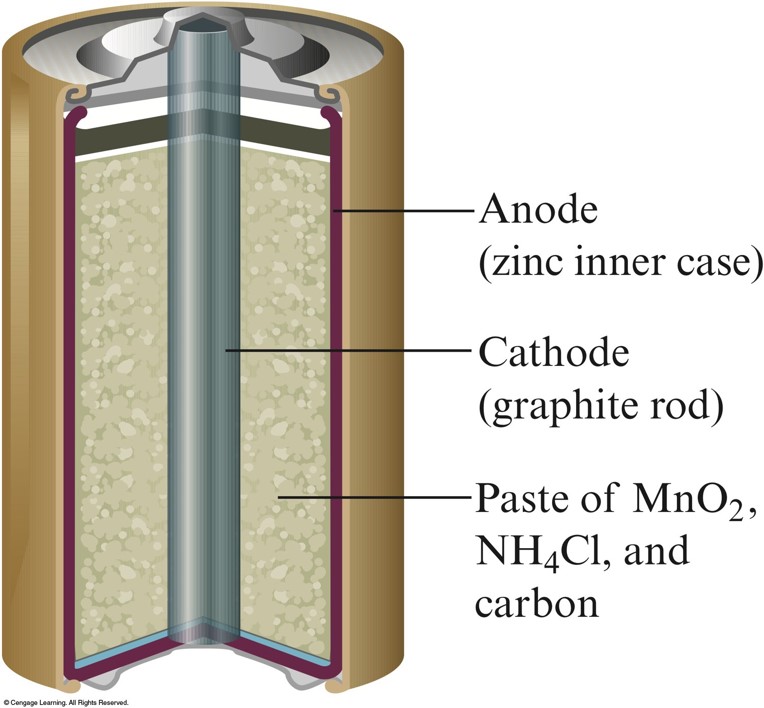
A Common Dry Cell Battery

Diagram showing a central graphite rod (the cathode) surrounded by a paste of manganese(IV) oxide, ammonium chloride, and carbon. Everything is encased in a zinc casing which acts as the anode.

A Mercury Battery

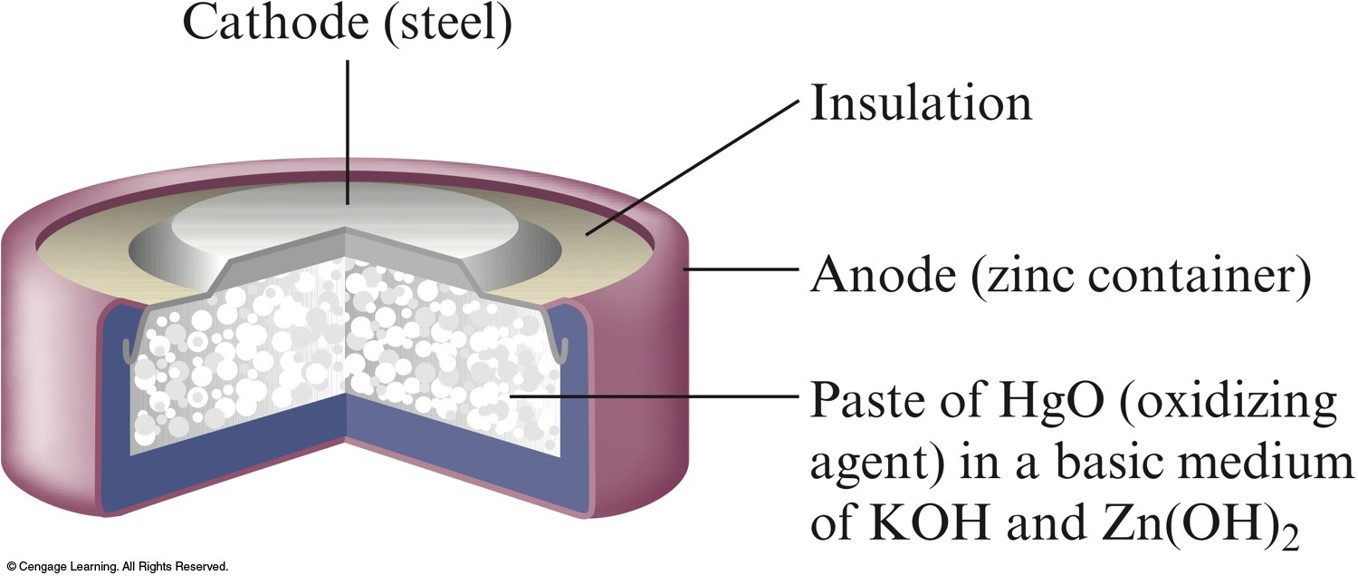
Diagram showing the top raised area of the battery acting as the cathode (made of steel) insulated from an outer casing of zinc which acts as the anode. Inside the casing is a paste of mercury(II) oxide in a basic medium of potassium hydroxide and zinc(II) hydroxide.

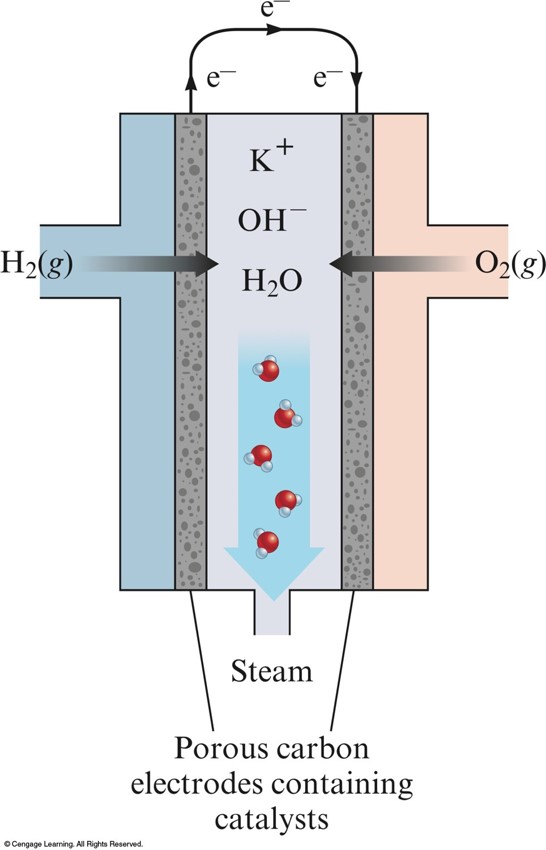
Schematic of the Hydrogen-Oxygen Fuel Cell

Hydrogen gas flows in through porous carbon from the left and oxygen gas flows in through porous carbon from the right. The gases react in the center forming water. A Wire connects the left and right porous carbon.

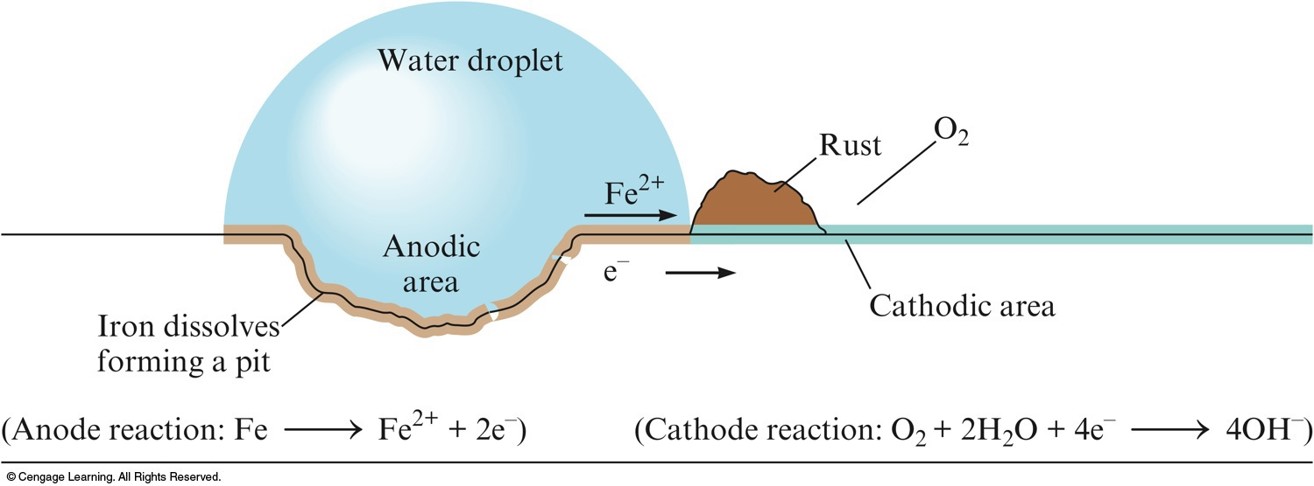
Corrosion

Process of returning metals to their natural state – the ores from which they were originally obtained.
Involves oxidation of the metal.

The corrosion of iron in a water droplet. The iron in contact with the water is acting as the anode while the iron around the water droplet is acting as the cathode.

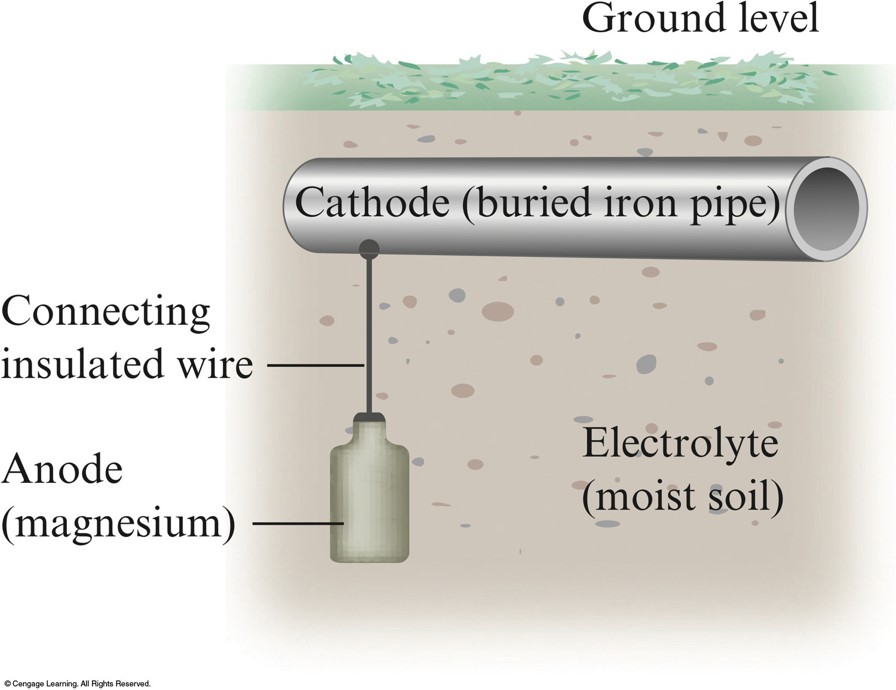
Corrosion Prevention

Application of a coating (like paint or metal plating)

Galvanizing

Alloying
Cathodic Protection

Protects steel in buried fuel tanks and pipelines.

Cathodic Protection

Buried iron pipes are protected from corrsion by connecting the pipe to a piece of magnesion. In the moist surrounding soil, the magnesium acts as an anode and the iron pipe acts as a cathode.

Electrolysis

Forcing a current through a cell to produce a chemical change for which the cell potential is negative.
Steps of stoichiometry of electrolysis

current and time $\rightarrow$ quantity of charge $$ \text{Coulombs of charge} = \text{current (C/s)} \times \text{time (s)} $$
quantity of charge $\rightarrow$ moles of electrons $$ \text{mole }e^- = \text{Coulombs of charge} \times \frac{1\,\mathrm{mol}\,e^-}{96485\,\mathrm{C}} $$
moles of electrons $\rightarrow$ moles of analyte
moles of analyte $\rightarrow$ grams of analyte

Concept Check

An unknown metal ($\chem{M}$) is electrolyzed. It took 52.8 sec for a current of 2.00 amp to plate 0.0719 g of the metal from a solution containing $\chem{M\left(NO_3\right)_3}$.

What is the metal?

gold (Au)

Commercial Electrolytic Processes

Production of aluminum
Purification of metals
Metal plating
Electrolysis of sodium chloride
Production of chlorine and sodium hydroxide

Producing Aluminum by the Hall-Heroult Process

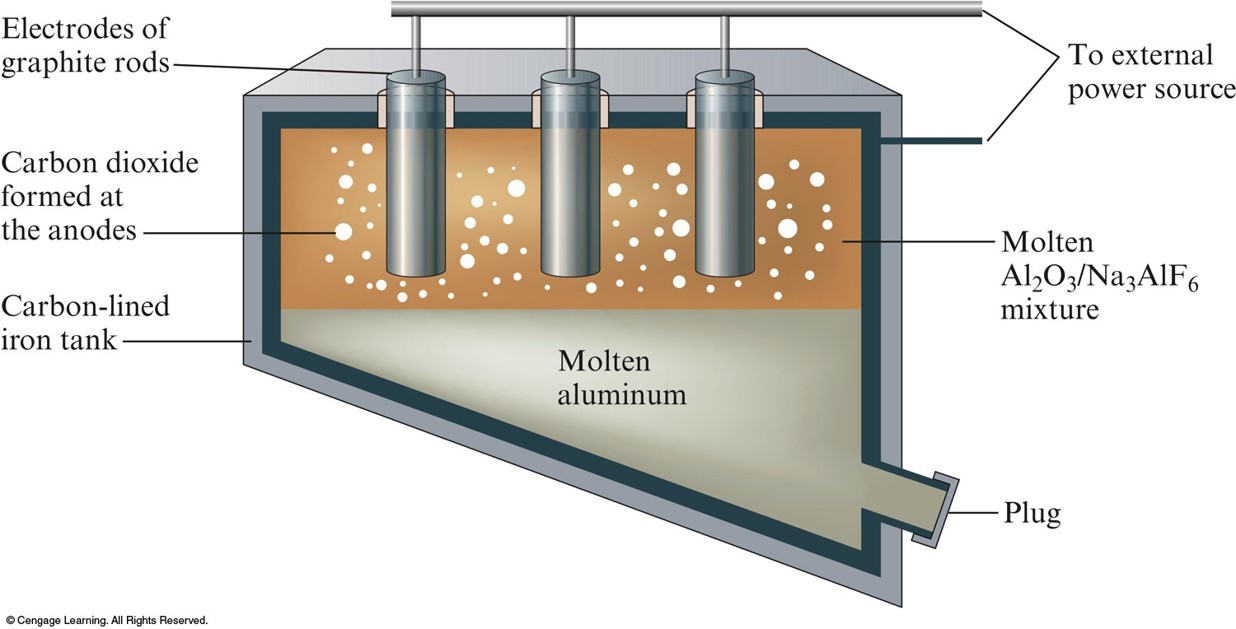
Graphite rodes are inserted through the top of a container into a molten mixture of aluminum oxide and sodium aluminum fluoride. Electricity applied between the graphite rodes and the container causes the aluminum to be reduced to liquid aluminum which sinks to the bottom. A plug in the botton of the container can be opened to extract the liquid aluminum metal.

Electroplating a Spoon

A piece of silver and a spoon are in a solution of silver ions. They are connected to a power supply with the spoon connected to the cathode. Turning on the power supply plates solid silver onto the cathode (spoon).

The Downs Cell for the Electrolysis of Molten Sodium Chloride

A diagram showing an anode and a cathode in moten sodium chloride. Chlorine gas is produced at the anode and molten sodium is produced at the cathode from which is can be extracted.

Chapter 17 Electrochemistry

Review of Terms

Half-Reactions

The Half–Reaction Method for Balancing Equations for Oxidation–Reduction Reactions Occurring in Acidic Solution

Example

Example Continued

Example Continued Further

Example Concluded

Exercise

The Half–Reaction Method for Balancing Equations for Oxidation–Reduction Reactions Occurring in Basic Solution

Galvantic Cell

The Galvantic Cell

Cell Potential

More on Galvanic Cells

Example: \(\chem{Fe^{3+}(aq) + Cu(s) → Cu^{2+}(aq) + Fe^{2+}(aq)}\)

Overall Balanced Cell Reaction

Line Notation

Description of a Galvanic Cell

Work

Maximum Cell Potential

A Concentration Cell

Nernst Equation

Exercise

Concept Check

One of the Six Cells in a 12–V Lead Storage Battery

A Common Dry Cell Battery

A Mercury Battery

Schematic of the Hydrogen-Oxygen Fuel Cell

Corrosion

Corrosion Prevention

Cathodic Protection

Electrolysis

Concept Check

Commercial Electrolytic Processes

Producing Aluminum by the Hall-Heroult Process

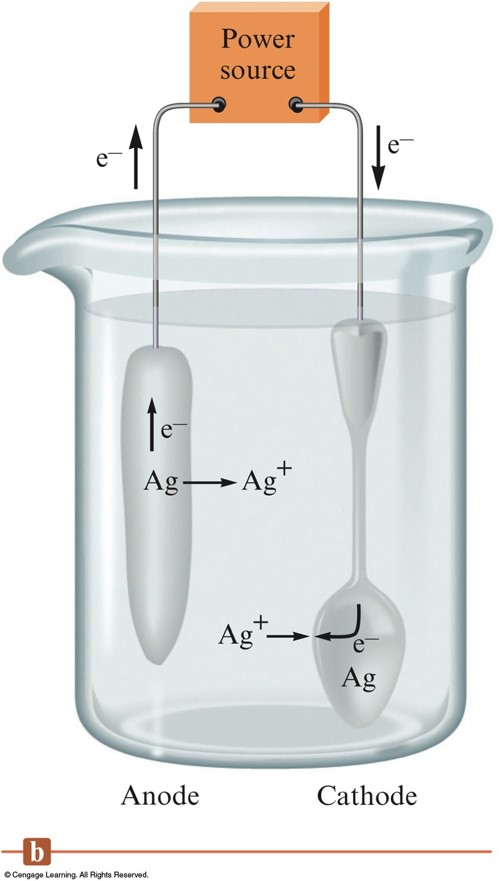
Electroplating a Spoon

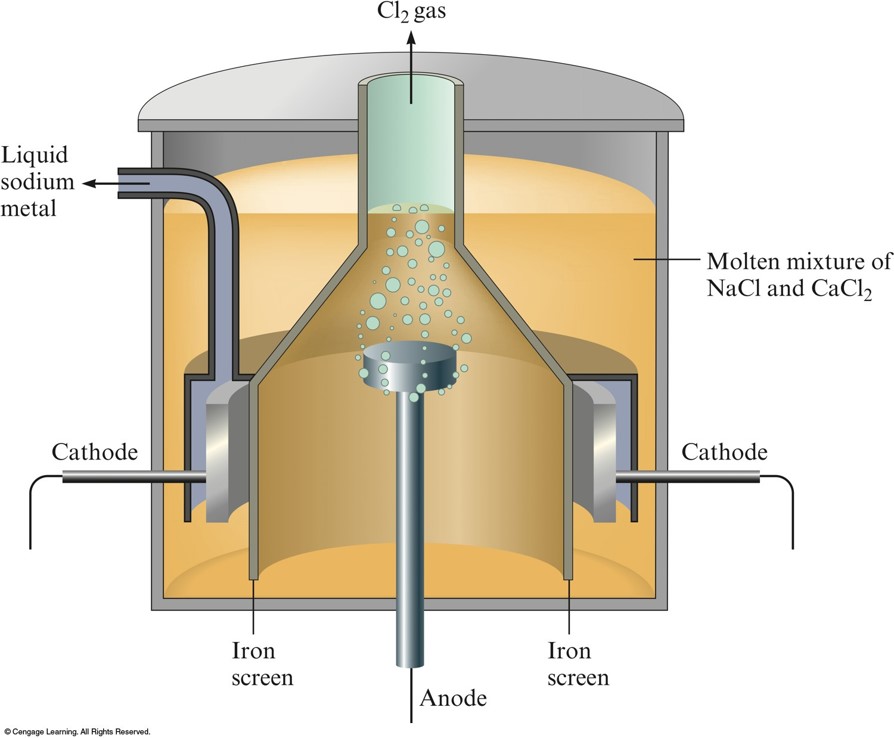
The Downs Cell for the Electrolysis of Molten Sodium Chloride

Chapter 17

Electrochemistry