Chapter 16

Thermodynamics

Shaun Williams, PhD

Thermodynamics vs. Kinetics

Domain of Kinetics

Rate of a reaction depends on the pathway from reactants to products.

Thermodynamics tells us whether a reaction is spontaneous based only on the properties of reactants and products.

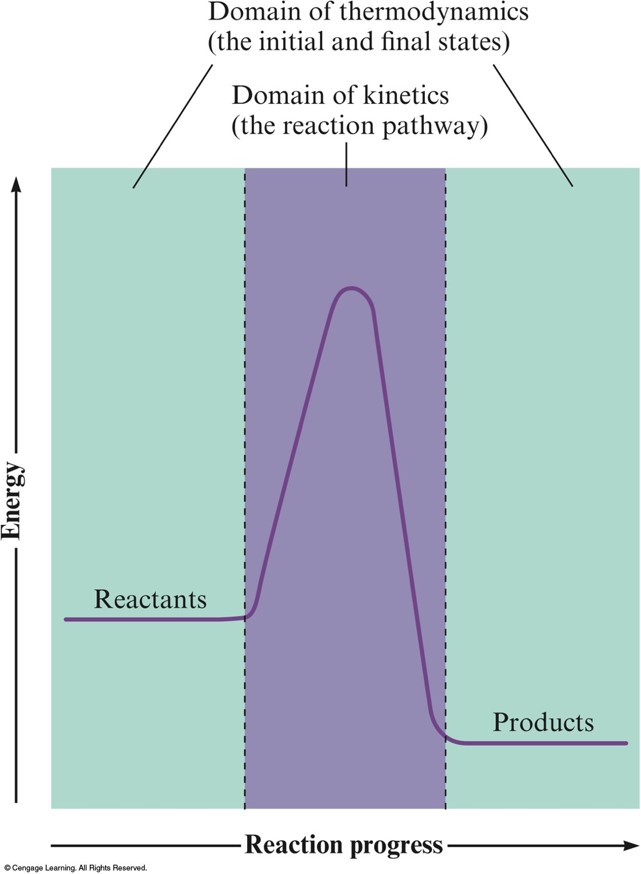
The energies of the reactants and products constitutes the thermodynamics domain. The energy profile from reactant to product constitutes the kinetic domain.

Spontaneous Processes and Entropy

Thermodynamics lets us predict the direction in which a process will occur but gives no information about the speed of the process.
A spontaneous process is one that occurs without outside intervention.

Concept Check

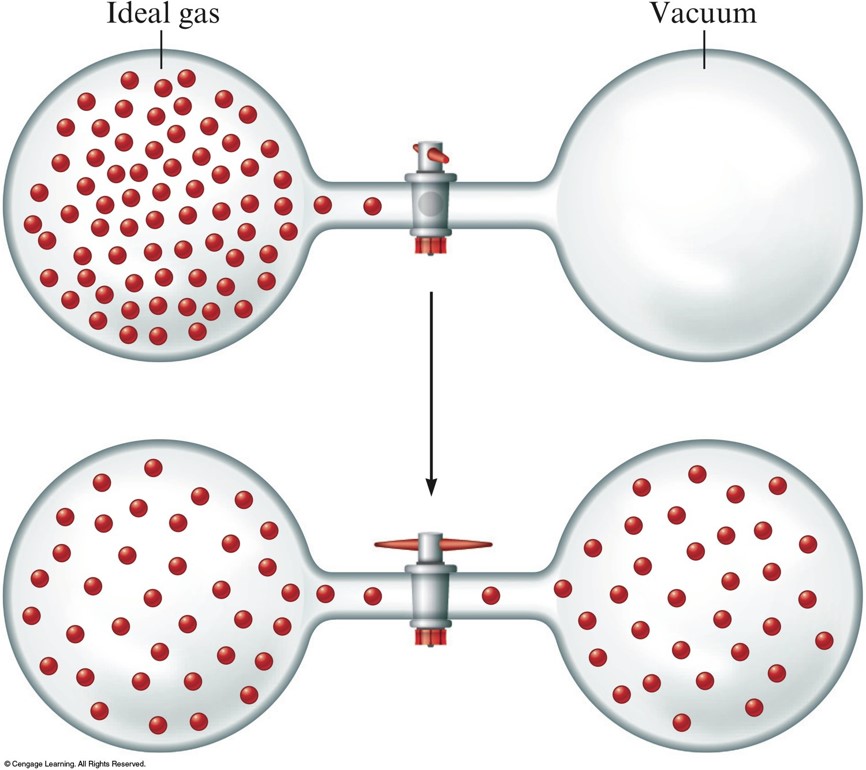
Consider $2.4\,\mathrm{moles}$ of a gas contained in a $4.0\,\mathrm{L}$ bulb at a constant temperature of $32^\circ \mathrm{C}$. This bulb is connected by a valve to an evacuated $20.0\,\mathrm{L}$ bulb. Assume the temperature is constant.

What should happen to the gas when you open the value?

The gas should spread evenly throughout the two bulbs.

The Expansion of an Ideal Gas Into an Evacuated Bulb

Two bulbs separated by a closed valve. Initally all the gas in contained in the left bulb and the right bulb is evacuated. When the valve is opened, the gas evenly distributes throughout both bulbs.

Entropy

The driving force for a spontaneous process is an increase in the entropy of the universe.
A measure of molecular randomness or disorder.
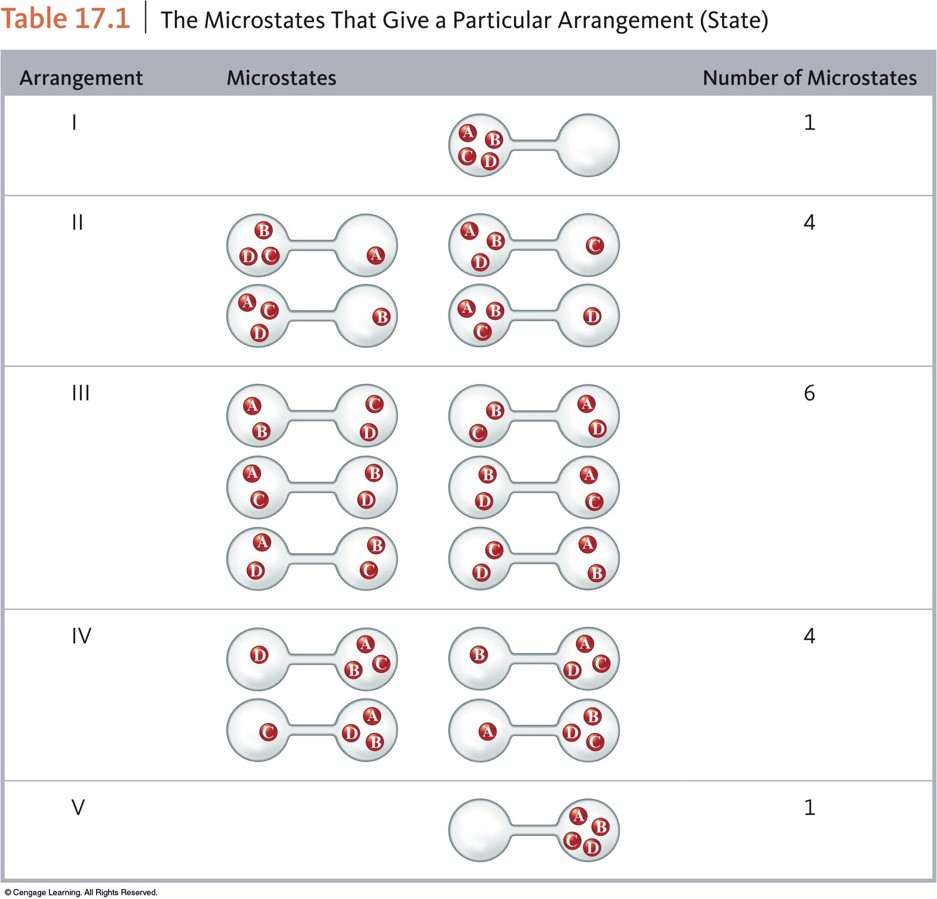
Thermodynamic function that describes the number of arrangements that are available to a system existing in a given state.
Nature spontaneously proceeds toward the states that have the highest probabilities of existing.

The Microstates That Give a Particular Arrangement (State)

The arrangement of 4 particles (each labeled) in the two bulbs with opened valve. There is one way to arrange them so that they are all in one bulb (one microstate). There are four ways to arrangement them so that 3 are in one bulb and one in the other (4 micrstate). Ther are 6 ways to arrange them so that two are in one bulb and two are in the other.

Positional Entropy

A gas expands into a vacuum to give a uniform distribution because the expanded state has the highest positional probability of states available to the system.
Therefore: $S_{solid} < S_{liquid} \ll S_{gas}$

The solid is highly ordered so it has a very low entropy. The liquid which is less ordered but still compact has a higher entropy. The gas is very disordered and spread out so it has a much higher entropy.

Concept Check

Predict the sign of $\Delta S$ for each of the following:

The evaporation of alcohol

positive

The freezing of water

negative

Compressing an ideal gas at constant temperature

negative

Heating an ideal gas at constant pressure

positive

Dissolving NaCl in water

positive

Second Law of Thermodynamics

In any spontaneous process there is always an increase in the entropy of the universe.
The entropy of the universe is increasing.
The total energy of the universe is constant, but the entropy is increasing.

$\Delta S_{surr}$

$\Delta S_{surr} > 0$: entropy of the universe increases
$\Delta S_{surr} < 0$: process is spontaneous in opposite direction
$\Delta S_{surr} = 0$: process has no tendency to occur
The sign of $\Delta S_{surr}$ depends on the direction of the heat flow.
The magnitude of $\Delta S_{surr}$ depends on the temperature.
Exothermic process: $ \Delta S_{surr} = +\frac{\text{quantity of heat (J)}}{\text{temperature (K)}} $
Endothermic process: $ \Delta S_{surr} = -\frac{\text{quantity of heat (J)}}{\text{temperature (K)}} $
Heat flow (constant $P$) = change in enthalpy = $\Delta H$ $$\Delta S_{surr}=-\frac{\Delta H}{T}$$

Interplay of $\Delta S_{sys}$ and $\Delta S_{surr}$ in Determining the Sign of $\Delta S_{univ}$

Signs of Entropy Changes
$\Delta S_{sys}$	$\Delta S_{surr}$	$\Delta S_{univ}$	Process Spontaneous?
+	+	+	Yes
-	-	-	No (reaction will occur in opposite direction)
+	-	?	Yes, if $\Delta S_{sys}$ has a larger magnitude than $\Delta S_{surr}$
-	+	?	Yes, if $\Delta S_{surr}$ has a larger magnitude than $\Delta S_{sys}$

Free Energy ($G$)

$$ \Delta S_{univ} = -\frac{\Delta G}{T}\,\left( \text{at constant }T\text{ and }P \right) $$

A process (at constant $T$ and $P$ is spontaneous in the direction in which the free energy decreases.
Negative $\Delta G$ means positive $\Delta S_{univ}$.
$ \Delta G = \Delta H - T\Delta S $ (at constant $T$ and $P$)

Effect of $\Delta H$ and $\Delta S$ on Spontaneity

Case	Result
$\Delta S > 0$, $\Delta H <0$	Spontaneous at all temperatures
$\Delta S > 0$, $\Delta H > 0$	Spontaneous at high temperatures (where exothermicity is relatively unimportant)
$\Delta S < 0$, $\Delta H < 0$	Spontaneous at low temperatures (where exothermicity is dominant)
$\Delta S < 0$, $\Delta H > 0$	Process not spontaneous at any temperatures (reverse process is spontaneous at all temperatures)

Third Law of Thermodynamics

The entropy of a perfect crystal at $0\,\mathrm{K}$ is zero.
The entropy of a substance increases with temperature.

Standard State Values

Standard Entropy Values ($S^\circ$)

Represent the increase in entropy that occurs when a substance is heated from $0\,\mathrm{K}$ to $298\,\mathrm{K}$ at 1 atm pressure. $$ \Delta S^\circ_{rxn} = \sum n_pS^\circ_{products} - \sum n_r S^\circ_{reactants} $$

Standard Free Energy Values ($\Delta G^\circ$)

The change in free energy that will occur if the reactants in their standard states are converted to the products in their standard states. $$ \Delta G^\circ = \Delta H^\circ - T\Delta S^\circ $$ $$ \Delta G^\circ_{rxn} = \sum n_p G^\circ_{products} - \sum n_r G^\circ_{reactants} $$

Concept Check

A stable diatomic molecule spontaneously forms from its atoms. Predict the sign of

$\Delta H^\circ$

negative

$\Delta S^\circ$

negative

$\Delta G^\circ$

negative

Free Energy

Free energy and pressure $$ \begin{align} G &= G^\circ + RT\ln (P) \\ &\mathrm{or} \\ \Delta G &= \Delta G^\circ + RT\ln (Q) \end{align} $$
Free energy and equilibrium $$ \Delta G=0=\Delta G^\circ + RT\ln (K) $$ $$ \Delta G^\circ = -RT \ln (K) $$

The Meaning of $\Delta G$ for a Chemical Reaction

A system can achieve the lowest possible free energy by going to equilibrium, not by going to completion.

When the energy profile of the reaction entirely downhill between reaction and product. If equilibrium is more stable then the reaction will not go to completion.

Change in Free Energy to Reach Equilibrium

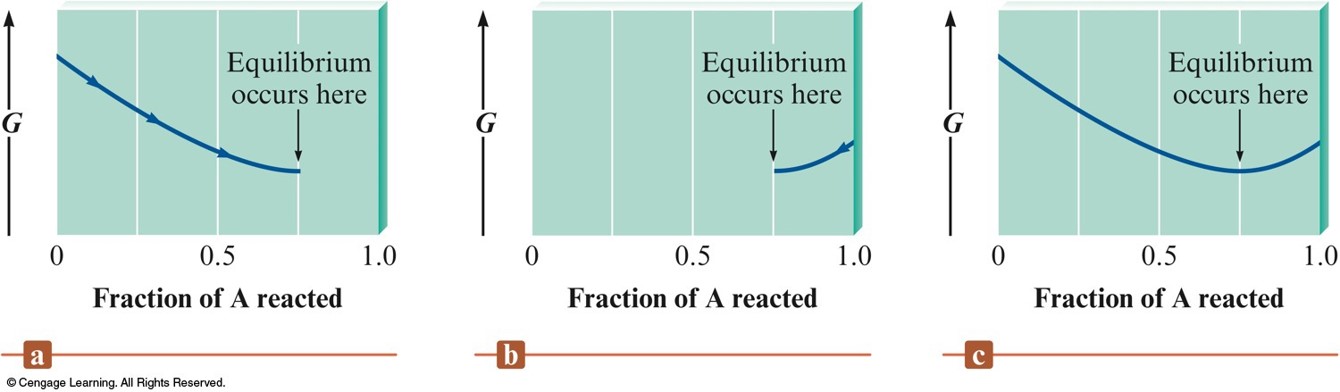
$Regardless of what fraction of reactant A you start with, the reaction will progress either forward or backward until an equilibrium is established.$

Qualitative Relationship Between the Change in Standard Free Energy and the Equilibrium Constant for a Given Reaction

$\Delta G^\circ$	$K$
$\Delta G^\circ = 0$	$K=1$
$\Delta G^\circ < 0$	$K>1$
$\Delta G^\circ > 0$	$K<1$

Free Energy and Work

Maximum possible useful work obtainable from a process at constant temperature and pressure is equal to the change in free energy. $$ w_{max} = \Delta G $$
Achieving the maximum work available from a spontaneous process can occur only via a hypothetical pathway. Any real pathway wastes energy.
All real processes are irreversible.
First law: You can’t win, you can only break even.
Second law: You can’t break even.
As we use energy, we degrade its usefulness.

Signs of Entropy Changes
\(\Delta S_{sys}\)	\(\Delta S_{surr}\)	\(\Delta S_{univ}\)	Process Spontaneous?
+	+	+	Yes
-	-	-	No (reaction will occur in opposite direction)
+	-	?	Yes, if \(\Delta S_{sys}\) has a larger magnitude than \(\Delta S_{surr}\)
-	+	?	Yes, if \(\Delta S_{surr}\) has a larger magnitude than \(\Delta S_{sys}\)

\(\Delta G^\circ\)	\(K\)
\(\Delta G^\circ = 0\)	\(K=1\)
\(\Delta G^\circ < 0\)	\(K>1\)
\(\Delta G^\circ > 0\)	\(K<1\)

Chapter 16

Thermodynamics

Thermodynamics vs. Kinetics

Spontaneous Processes and Entropy

Concept Check

The Expansion of an Ideal Gas Into an Evacuated Bulb

Entropy

The Microstates That Give a Particular Arrangement (State)

Positional Entropy

Concept Check

Second Law of Thermodynamics

\(\Delta S_{surr}\)

Interplay of \(\Delta S_{sys}\) and \(\Delta S_{surr}\) in Determining the Sign of \(\Delta S_{univ}\)

Free Energy (\(G\))

Effect of \(\Delta H\) and \(\Delta S\) on Spontaneity

Third Law of Thermodynamics

Standard State Values

Concept Check

Free Energy

The Meaning of \(\Delta G\) for a Chemical Reaction

Change in Free Energy to Reach Equilibrium

Qualitative Relationship Between the Change in Standard Free Energy and the Equilibrium Constant for a Given Reaction

Free Energy and Work

Case	Result
\(\Delta S > 0\), \(\Delta H <0\)	Spontaneous at all temperatures
\(\Delta S > 0\), \(\Delta H > 0\)	Spontaneous at high temperatures (where exothermicity is relatively unimportant)
\(\Delta S < 0\), \(\Delta H < 0\)	Spontaneous at low temperatures (where exothermicity is dominant)
\(\Delta S < 0\), \(\Delta H > 0\)	Process not spontaneous at any temperatures (reverse process is spontaneous at all temperatures)

Chapter 16 Thermodynamics

Thermodynamics vs. Kinetics

Spontaneous Processes and Entropy

Concept Check

The Expansion of an Ideal Gas Into an Evacuated Bulb

Entropy

The Microstates That Give a Particular Arrangement (State)

Positional Entropy

Concept Check

Second Law of Thermodynamics

\(\Delta S_{surr}\)

Interplay of \(\Delta S_{sys}\) and \(\Delta S_{surr}\) in Determining the Sign of \(\Delta S_{univ}\)

Free Energy (\(G\))

Effect of \(\Delta H\) and \(\Delta S\) on Spontaneity

Third Law of Thermodynamics

Standard State Values

Concept Check

Free Energy

The Meaning of \(\Delta G\) for a Chemical Reaction

Change in Free Energy to Reach Equilibrium

Qualitative Relationship Between the Change in Standard Free Energy and the Equilibrium Constant for a Given Reaction

Free Energy and Work

Chapter 16

Thermodynamics