Chapter 15

Equilibria of Other Reaction Classes

Shaun Williams, PhD

Solubility Equilibria

• Solubility product (\(K_{sp}\)) – equilibrium constant; has only one value for a given solid at a given temperature.
• Solubility – an equilibrium position.
$$ \chem{Bi_2S_3(s) \rightleftharpoons 2Bi^{3+}(aq) + 3S^{2-}(aq)} $$ $$ K_{sp}=\conc{Bi^{3+}}^2\conc{S^{2-}}^3 $$

Exercise

Calculate the solubility of silver chloride in water. \(K_{sp} = 1.6 \times 10^{–10}\)

\(1.3 \times 10^{-5}\,\mathrm{M}\)

Calculate the solubility of silver phosphate in water. \(K_{sp} = 1.8 \times 10^{–18}\)

\(1.6 \times 10^{-5}\,\mathrm{M}\)

Exercise

Calculate the solubility of \(\chem{AgCl}\) in: $$ K_{sp}=1.6 \times 10^{-10} $$

1. \(100.0\,\mathrm{mL}\) of \(4.00 \times 10^{-3}\,\mathrm{M}\) calcium chloride.

\(2.0 \times 10^{-8}\,\mathrm{M}\)

2. \(100.0\,\mathrm{mL}\) of \(4.00 \times 10^{-3}\,\mathrm{M}\) calcium nitrate.

\(1.3 \times 10^{-5}\,\mathrm{M}\)

Precipitation (Mixing Two Solutions on Ions)

• \(Q > K_{sp}\): precipitation occurs and will continue until the concentrations are reduced to the point that they satisfy \(K_{sp}\).
• \(Q < K_{sp}\): no precipitation occurs.
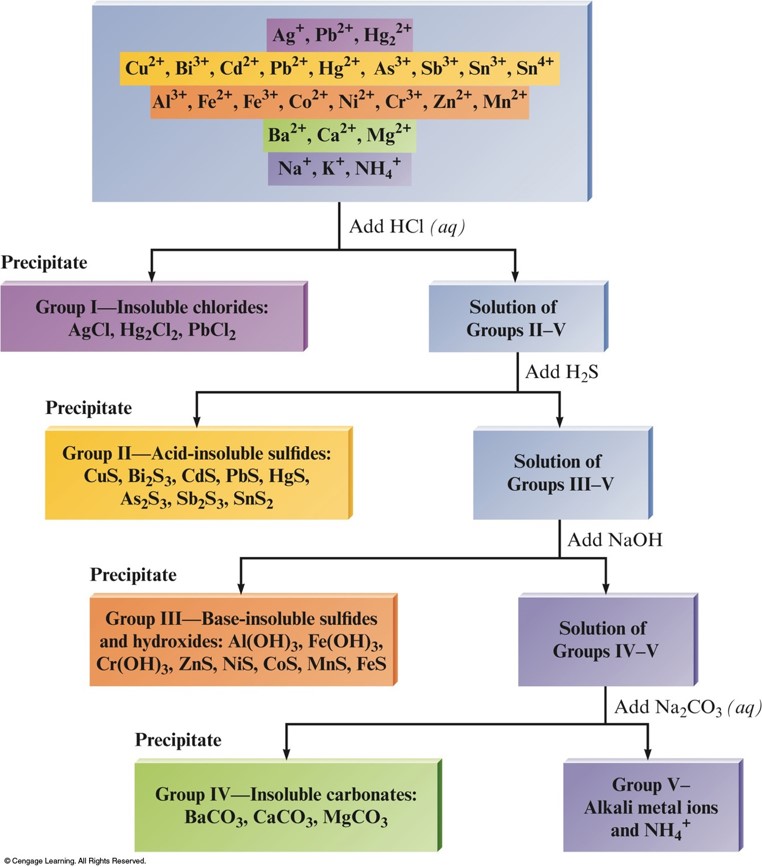
• Selective Precipitation (Mixtures of Metal Ions)
• Use a reagent whose anion forms a precipitate with only one or a few of the metal ions in the mixture.
• Example:
• Solution contains \(\chem{Ba^{2+}}\) and \(\chem{Ag^+}\) ions.
• Adding \(\chem{NaCl}\) will form a precipitate with \(\chem{Ag^+}\) (\(\chem{AgCl}\)), while still leaving \(\chem{Ba^{2+}}\) in solution.

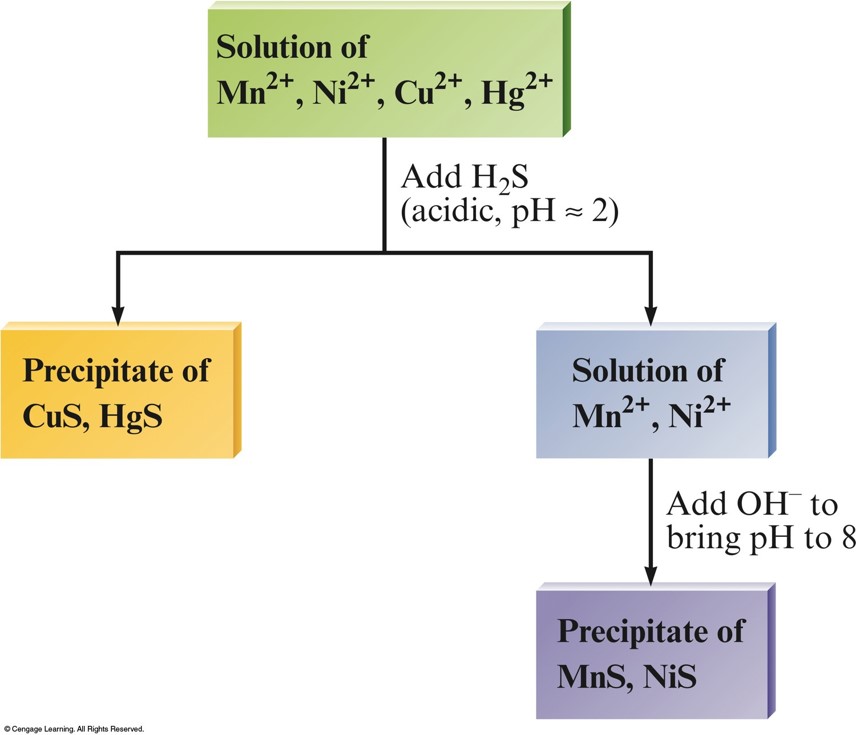
Separation of \(\chem{Cu^{2+}}\) and \(\chem{Hg^{2+}}\) from \(\chem{Ni^{2+}}\) and \(\chem{Mn^{2+}}\) using \(\chem{H_2S}\)

• At a low \(\mathrm{pH}\), \(\conc{S^{2-}}\) is relatively low and only the very insoluble \(\chem{HgS}\) and \(\chem{CuS}\) precipitate.
• When \(\chem{OH^–}\) is added to lower \(\conc{H^+}\), the value of \(\conc{S^{2-}}\) increases, and \(\chem{MnS}\) and \(\chem{NiS}\) precipitate.

Separation of \(\chem{Cu^{2+}}\) and \(\chem{Hg^{2+}}\) from \(\chem{Ni^{2}}\) and \(\chem{Mn^{2+}}\) using \(\chem{H_2S}\)

Separating the Common Cations by Selective Precipitation

Complex Ion Equilibria

• Charged species consisting of a metal ion surrounded by ligands.
• Ligand: Lewis base
• Formation (stability) constant.
• Equilibrium constant for each step of the formation of a complex ion by the addition of an individual ligand to a metal ion or complex ion in aqueous solution.

Complex Ions and Solubility

• Two strategies for dissolving a water–insoluble ionic solid.
• If the anion of the solid is a good base, the solubility is greatly increased by acidifying the solution.
• In cases where the anion is not sufficiently basic, the ionic solid often can be dissolved in a solution containing a ligand that forms stable complex ions with its cation.

Concept Check

Calculate the solubility of silver chloride in 10.0 M ammonia given the following information: $$ K_{sp}(\chem{AgCl}) = 1.6 \times 10^{-10} $$ $$ \begin{align} &\chem{Ag^++NH_3 \rightleftharpoons AgNH_3^+} &~~~~& K = 2.1 \times 10^3 \\ &\chem{AgNH_3^++NH_3 \rightleftharpoons Ag\left( NH_3\right)_2^+} &~~~~& K = 8.2 \times 10^3 \end{align} $$

\(0.48\,\mathrm{M}\)

Calculate the concentration of \(\chem{NH_3}\) in the final equilibrium mixture.

\(9.0\,\mathrm{M}\)