Chapter 14

Acid-Base Equilibria

Shaun Williams, PhD

Models of Acids and Bases

Arrhenius: Acids produce $\chem{H^+}$ ions in solution, bases produce $\chem{OH^-}$ ions.
Brønsted-Lowry: Acids are proton ($\chem{H^+}$) donors, bases are proton acceptors.

$$ \chem{\underbrace{HCl}_{acid} + \underbrace{H_2O}_{base} \rightleftharpoons Cl^- + H_3O^+} $$

Acid in Water

$$ \chem{\underbrace{HA(aq)}_{Acid} + \underbrace{H_2O(l)}_{Base} \rightleftharpoons \underbrace{H_3O^+(aq)}_{\text{Conjugate acid}} + \underbrace{A^-(aq)}_{\text{Conjugate base}}} $$

Conjugate base is everything that remains of the acid molecule after a proton is lost.
Conjugate acid is formed when the proton is transferred to the base.

Acid Strength

Strong acid:

Ionization equilibrium lies far to the right.
Yields a weak conjugate base.

Weak acid:

Ionization equilibrium lies far to the left.
Weaker the acid, stronger its conjugate base.

Acid Strength

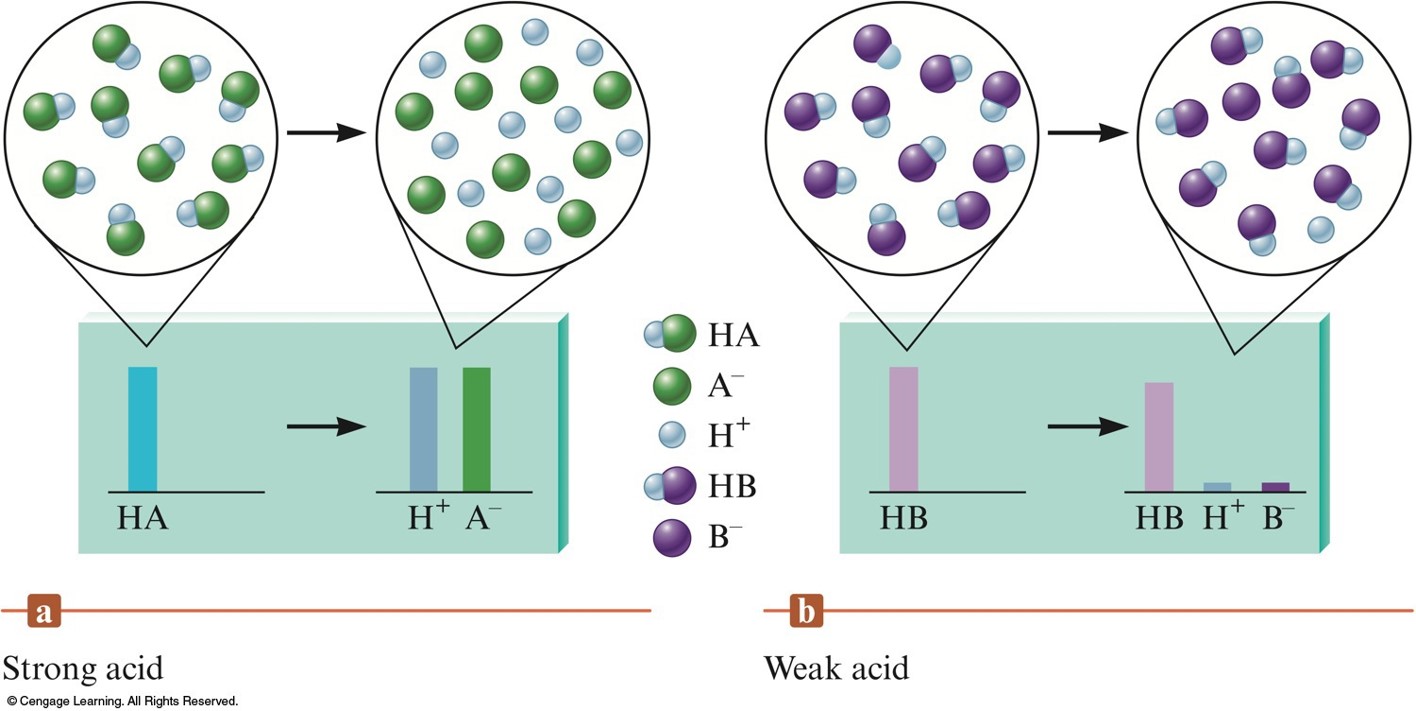
$100% of strong acids molecules in water break up into their ions. Only a small fraction of weak acid molecules break up into their ions in water.$

Various Ways to Describe Acid Strength

Property	Strong Acid	Weak Acid
$K_a$ value	$K_a$ is large	$K_a$ is small
Position of the dissociation (ionization) equilibrium	Far to the right	Far to the left
Equilibrium concentration of $\conc{H^+}$ compared with original	$\conc{H^+}\approx \conc{HA}_0$	$\conc{H^+}\ll \conc{HA}_0$
Strength of conjugate base compared with that of water	$\chem{A^-}$ much weaker base than $\chem{H_2O}$	$\chem{A^-}$ much stronger base than $\chem{H_2O}$

Water as an Acid and a Base

Water is amphoteric:

Behaves either as an acid or as a base.

At $25^\circ\mathrm{C}$: $$ K_w = \conc{H^+}\conc{OH^-} = 1.0 \times 10^{–14} $$
No matter what the solution contains, the product of $\conc{H^+}$ and $\conc{OH^-}$ must always equal $1.0 \times 10^{-14}$ at $25^\circ\mathrm{C}$.
Three possible situations:

$\conc{H^+}=\conc{OH^-}$: neutral solution
$\conc{H^+}>\conc{OH^-}$: acidic solution
$\conc{OH^-}>\conc{H^+}$: basic solution

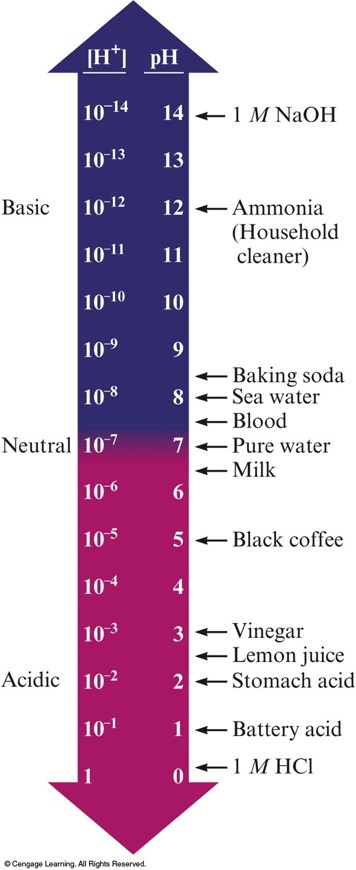
The pH Scale

$pH = –\log\conc{H^+}$
pH changes by 1 for every power of 10 change in $\conc{H^+}$.
A compact way to represent solution acidity.
pH decreases as $\conc{H^+}$ increases.
Significant figures:

The number of decimal places in the log is equal to the number of significant figures in the original number.

pH Range

$pH = 7$: neutral
$pH > 7$: basic
$pH < 7$: acidic

The pH Scale and pH Values of Some Common Substances

A scale showing 1 M HCl at a pH of 1 up to 1 M NaOH at a pH of 14.

Exercise

Calculate the pH for each of the following solutions.

$1.0 \times 10^{-4}\,\mathrm{M}\,\chem{H^+}$

$pH=4.00$

$0.0400\,\mathrm{M}\,\chem{OH^-}$

$pH=12.60$

pH and pOH

Recall:

$$ K_w=\conc{H^+}\conc{OH^-} $$ $$ -\log K_w = -\log \conc{H^+} - \log \conc{OH^-} $$ $$ \mathrm{p}K_w=\mathrm{pH}+\mathrm{pOH} $$ $$ 14.00 = \mathrm{pH} + \mathrm{pOH} $$

Exercise

Calculate the pOH for each of the following solutions.

$ 1.0 \times 10^{-4}\,\mathrm{M}\,\chem{H^+} $

$\mathrm{pOH}=10.00$

$ 0.040\,\mathrm{M}\,\chem{OH^-} $

$\mathrm{pOH}=1.40$

Exercise

The pH of a solution is 5.85. What is the [OH–] for this solution?

$ \conc{OH^-}=7.1\times 10^{-9}\,\mathrm{M} $

Thinking About Acid-Base Problems

What are the major species in solution?
What is the dominant reaction that will take place?

Is it an equilibrium reaction or a reaction that will go essentially to completion?
React all major species until you are left with an equilibrium reaction.

Solve for the pH if needed.

Concept Check

Calculate the pH of a $ 1.5 \times 10^{–11}\,\mathrm{M} $ solution of $\chem{HCl}$.

$\mathrm{pH}=7.00$

Concept Check

Calculate the pH of a $ 1.5 \times 10^{–2}\,\mathrm{M} $ solution of $\chem{HNO_3}$.

$\mathrm{pH}=1.82$

Solving Weak Acid Equilibrium Problems

List the major species in the solution.
Choose the species that can produce $\chem{H^+}$, and write balanced equations for the reactions producing $\chem{H^+}$.
Using the values of the equilibrium constants for the reactions you have written, decide which equilibrium will dominate in producing $\chem{H^+}$.
Write the equilibrium expression for the dominant equilibrium.
List the initial concentrations of the species participating in the dominant equilibrium.
Define the change needed to achieve equilibrium; that is, define $x$.
Write the equilibrium concentrations in terms of $x$.
Substitute the equilibrium concentrations into the equilibrium expression.

Solving Weak Acid Equilibrium Problems (cont.)

Solve for $x$ the “easy” way, that is, by assuming that $\conc{HA}_0-x$ about equals $\conc{HA}_0$.
Use the 5% rule to verify whether the approximation is valid.
Calculate $\conc{H^+}$ and $\mathrm{pH}$.

Consider This

$$\begin{align} \chem{HCN(aq)+H_2O(l)} &\rightleftharpoons \chem{H_3O^+(aq)+CN^-(aq)} & K_a&=6.2 \cdot 10^{-1} \\ \chem{H_2O(l)+H_2O(l)} &\rightleftharpoons \chem{H_3O^+(aq)+OH^-(aq)} & K_w&=1.0 \cdot 10^{-14} \end{align}$$ Which reaction controls the pH? Explain.

Exercise

Calculate the pH of a $0.50\,\mathrm{M}$ aqueous solution of the weak acid $\chem{HF}$. ($K_a=7.2\times 10^{-4}$)

$$ \begin{align} & \chem{HF(aq)} &+& \chem{H_2O} &\rightleftharpoons& \chem{H_3O^+(aq)} &+& \chem{F^-(aq)} \\ \mathrm{Initial}\;\; & 0.50\,\mathrm{M} && - && \sim 0 && \sim 0 \\ \mathrm{Change}\;\; & -x && - && +x && +x \\ \mathrm{Equilibrium}\;\; & 0.50-x && - && x && x \\ \end{align} $$ $$ \mathrm{pH}=1.72 $$

Percent Dissociation (Ionization)

$$ \text{Percent dissociation}=\frac{\text{amount dissociated}\,\left(\bfrac{\mathrm{mol}}{\mathrm{L}}\right)}{\text{initial concentration}\,\left(\bfrac{\mathrm{mol}}{\mathrm{L}}\right)} \times 100% $$

For a given weak acid, the percent dissociation increases as the acid becomes more dilute.

Exercise

A solution of $8.00\,\mathrm{M}$ formic acid ($\chem{HCHO_2}$) is 0.47% ionized in water.

Calculate the $K_a$ value for formic acid.

$$ K_a=1.8 \times 10^{-4} $$

Exercise

Calculate the pH of an $8.00\,\mathrm{M}$ solution of formic acid. Use the data from the previous slide to help you solve this problem.

$$ \mathrm{pH}=1.42 $$

Bases

Arrhenius: bases produce $\chem{OH^–}$ ions.
Brønsted–Lowry: bases are proton acceptors.
In a basic solution at $25^\circ \mathrm{C}$, $\mathrm{pH}>7.$
Ionic compounds containing $\chem{OH^-}$ are generally considered strong bases.
$\chem{LiOH}$, $\chem{NaOH}$, $\chem{KOH}$, $\chem{Ca(OH)_2}$
$\mathrm{pOH} = –\log\conc{OH^-}$
$\mathrm{pH} = 14.00 – \mathrm{pOH}$

Concept Check

Calculate the $\mathrm{pH}$ of a $ 1.0 \times 10^{–3}\,\mathrm{M} $ solution of sodium hydroxide.

$$ \mathrm{pH}=11.00 $$

Concept Check

Calculate the $\mathrm{pH}$ of a $ 1.0 \times 10^{–3}\,\mathrm{M} $ solution of calcium hydroxide.

$$ \mathrm{pH}=11.30 $$

Weak Bases

Equilibrium expression for weak bases uses $K_n$.
$\mathrm{pH}$ calculations for solutions of weak bases are very similar to those for weak acids.
$K_w = \conc{H^+}\conc{OH^-} = 1.0 \times 10^{–14}$
$\mathrm{pOH} = –\log\conc{OH^-}$
$\mathrm{pH} = 14.00 – \mathrm{pOH}$

Concept Check

Calculate the $\mathrm{pH}$ of a $ 2.0\,\mathrm{M} $ solution of ammonia ($\chem{NH_3}$). $$(K_b=1.8 \times 10^{-5})$$

$$ \mathrm{pH}=11.78 $$

Polyprotic Acids

Acids that can furnish more than one proton.
Always dissociates in a stepwise manner, one proton at a time.
The conjugate base of the first dissociation equilibrium becomes the acid in the second step.
For a typical weak polyprotic acid: $K_{a1} > K_{a2} > K_{a3}$
For a typical polyprotic acid in water, only the first dissociation step is important to $\mathrm{pH}$.

Exercise

Calculate the $\mathrm{pH}$ of a $ 1.00\,\mathrm{M} $ solution of $\chem{H_3PO_4}$. $$ \begin{align} K_{a1} &= 7.5 \times 10^{-3} \\ K_{a2} &= 6.2 \times 10^{-8} \\ K_{a3} &= 4.8 \times 10^{-13} \end{align} $$

$$ \mathrm{pH}=1.08 $$

Concept Check

Calculate the equilibrium concentration of $\chem{PO_4^{3-}}$ in a $ 1.00\,\mathrm{M} $ solution of $\chem{H_3PO_4}$. $$ \begin{align} K_{a1} &= 7.5 \times 10^{-3} \\ K_{a2} &= 6.2 \times 10^{-8} \\ K_{a3} &= 4.8 \times 10^{-13} \end{align} $$

$$ \conc{PO_4^{3-}}=3.6 \times 10^{-19}\,\mathrm{M} $$

Salts

Ionic compounds.
When dissolved in water, break up into its ions (which can behave as acids or bases).
The salt of a strong acid and a strong base gives a neutral solution.

$\chem{KCl}$, $\chem{NaNO_3}$

A basic solution is formed if the anion of the salt is the conjugate base of a weak acid.

$\chem{NaF}$, $\chem{KC_2H_3O_2}$
$K_w = K_a \times K_b$

Use $K_b$ when starting with base.

More of Salts

An acidic solution is formed if the cation of the salt is the conjugate acid of a weak base.

$\chem{NH_4Cl}$
$K_w = K_a \times K_b$

Use $K_a$ when starting with acid.

Summary of Properties of Salts

Cation	Anion	Acidic or Basic	Example
neutral	neutral	neutral	$\chem{NaCl}$
neutral	conjugate base of weak acid	basic	$\chem{NaF}$
conjugate acid of a weak base	neutral	acidic	$\chem{NH_4Cl}$
conjugate acid of a weak base	conjugate acid of a weak acid	depends on $K_a$ & $K_b$ values	$\chem{Al_2(SO_4)_3}$

Qualitative Prediction of pH of Salt Solutions (from Weak Parents)

$K_a>K_b$	$\mathrm{pH}<7$ (acidic)
$K_b>K_a$	$\mathrm{pH}>7$ (basic)
$K_a=K_b$	$\mathrm{pH}=7$ (neutral)

Exercise

Calculate the $\mathrm{pH}$ of a $0.75\,\mathrm{M}$ aqueous solution of $\chem{NaCN}$.$K_a$ for $\chem{HCN}$ is $6.2 \times 10^{–10}$.

$$ \begin{align} & \chem{CN^-(aq)} &+& \chem{H_2O} &\rightleftharpoons& \chem{HCN(aq)} &+& \chem{OH^-(aq)} \\ \mathrm{Initial}\;\; & 0.75\,\mathrm{M} && - && 0 && \sim 0 \\ \mathrm{Change}\;\; & -x && - && +x && +x \\ \mathrm{Equilibrium}\;\; & 0.75-x && - && x && x \\ \end{align} $$ $$ \mathrm{pH}=11.54 $$

Models of Acids and Bases

Two factors for acidity in binary compounds:

Bond Polarity (high is good)
Bond Strength (low is good)

H-X Bond	Bond Strength (kJ/mol)	Acid Strength in Water
H-F	565	Weak
H-Cl	427	Strong
H-Br	363	Strong
H-I	295	Strong

Oxyacids

Contains the group H–O–X.
For a given series the acid strength increases with an increase in the number of oxygen atoms attached to the central atom.
The greater the ability of X to draw electrons toward itself, the greater the acidity of the molecule.

Comparison of Electronegativitiy of X and $K_a$ Value for a Series of Oxyacids

Acid	X	Electronegativity of X	$K_a$ for Acid
$\chem{HOCl}$	$\chem{Cl}$	3.0	$ 4 \times 10^{-8} $
$\chem{HOBr}$	$\chem{Br}$	2.8	$ 2 \times 10^{-9} $
$\chem{HOI}$	$\chem{I}$	2.5	$ 2 \times 10^{-11} $
$\chem{HOCH_3}$	$\chem{CH_3}$	2.3 (for carbon $\chem{CH_3}$)	$ \sim 10^{-15} $

Oxides

Acidic Oxides (Acid Anhydrides):

O—X bond is strong and covalent. $$ \chem{SO_2}, \chem{NO_2}, \chem{CO_2}$$

When H—O—X grouping is dissolved in water, the O—X bond will remain intact. It will be the polar and relatively weak H—O bond that will tend to break, releasing a proton.
Basic Oxides (Basic Anhydrides):

O—X bond is ionic. $$ \chem{K_2O}, \chem{CaO} $$

If X has a very low electronegativity, the O—X bond will be ionic and subject to being broken in polar water, producing a basic solution.

Lewis Acids and Bases

Lewis acid: electron pair acceptor
Lewis base: electron pair donor

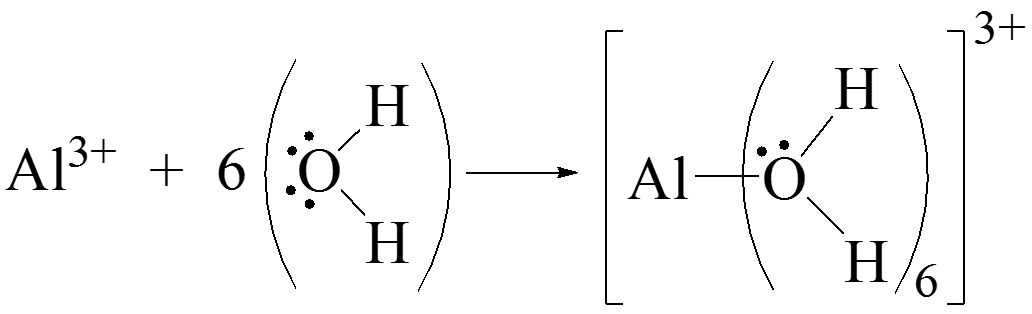
A pictoral representation of aluminum ion with six waters to form the aluminum hexahydrate ion with a plus 3 charge.

In the above reaction, $\chem{Al^{3+}}$ is acting as a Lewis acid.
In the above reaction, $\chem{H_2O}$ is acting as a Lewis base.

Three Models for Acids and Bases

Model	Definition of Acid	Definition of Base
Arrhenius	$\chem{H^+}$ producer	$\chem{OH^-}$ producer
Brønsted-Lowry	$\chem{H^+}$ donor	$\chem{H^+}$ acceptor
Lewis	Electron-pair acceptor	Electron-pair donor

When analyzing an acid-base equilibrium problem:

Ask this question: What are the major species in the solution and what is their chemical behavior?

What major species are present?
Does a reaction occur that can be assumed to go to completion?
What equilibrium dominates the solution?
Let the problem guide you. Be patient.

Common Ion Effect

Shift in equilibrium position that occurs because of the addition of an ion already involved in the equilibrium reaction.
An application of Le Châtelier’s principle.
Addition of $\chem{NaCN}$ will shift the equilibrium to the left because of the addition of $\chem{CN^-}$, which is already involved in the equilibrium reaction.
A solution of $\chem{HCN}$ and $\chem{NaCN}$ is less acidic than a solution of $\chem{HCN}$ alone.

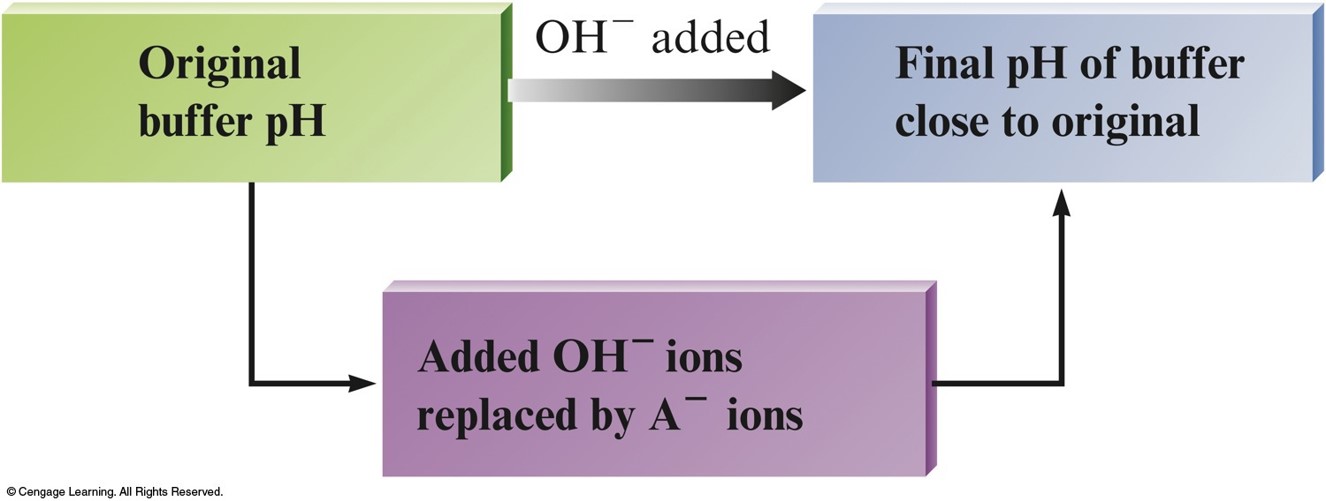
Key Points about Buffered Solutions

Buffered Solution – resists a change in pH.
They are weak acids or bases containing a common ion.
After addition of strong acid or base, deal with stoichiometry first, then the equilibrium.

Solving Problems with Buffered Solution

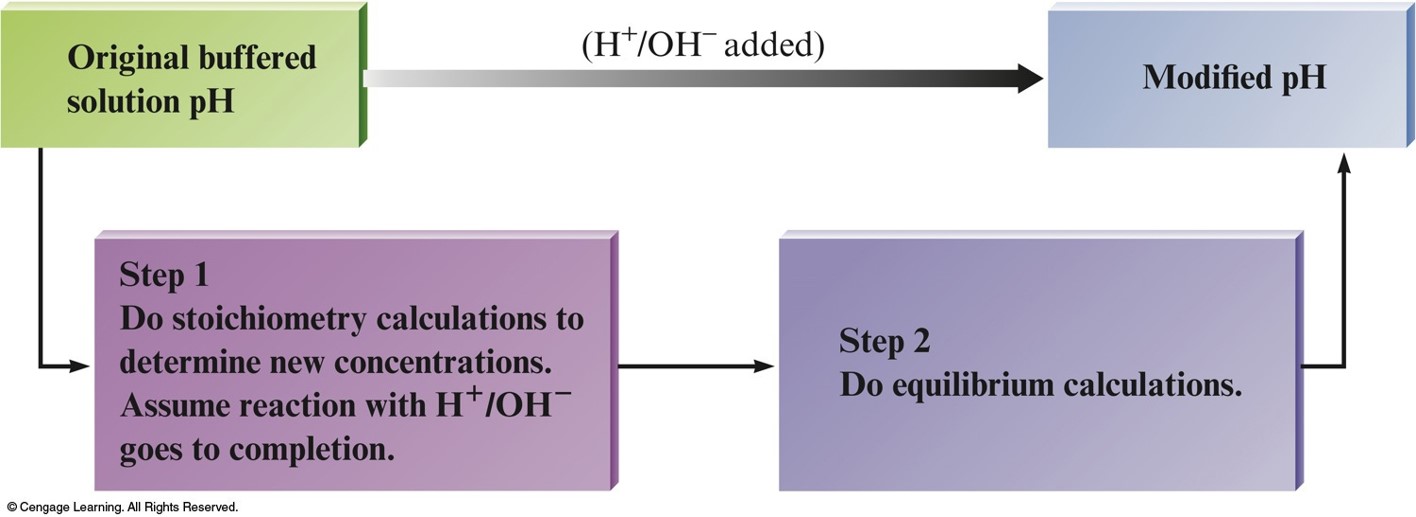
In order to go from original buffered solution pH to the modified pH with the addition of an acid or base you first assume the added acid or base totally reacts with the buffer then perform the equilibrium calculation with these new concentrations.

Buffering: How Does It Work?

Adding hydroxide ions replaced by the conjugate base from the original buffer system therefore the final pH of the system will be close to that of the original buffer.

Henderson-Hasselbalch Equation

$$ \mathrm{pH} = \mathrm{p}K_a + \log \frac{\conc{A^-}}{\conc{HA}} $$

For a particular buffering system (conjugate acid–base pair), all solutions that have the same ratio $\frac{\conc{A^-}}{\conc{HA}}$ will have the same $\mathrm{pH}$.

Exercise

What is the $\mathrm{pH}$ of a buffer solution that is $0.45\,\mathrm{M}$ acetic acid ($\chem{HC_2H_3O_2}$) and $0.85\,\mathrm{M}$ sodium acetate ($\chem{NaC_2H_3O_2}$)? The $K_a$ for acetic acid is $1.8 \times 10^{–5}$.

$ \mathrm{pH} = 5.02 $

Buffered Solution Characteristics

Buffers contain relatively large concentrations of a weak acid and corresponding conjugate base.
Added $\chem{H^+}$ reacts to completion with the weak base.
Added $\chem{OH^-}$ reacts to completion with the weak acid.
The $\mathrm{pH}$ in the buffered solution is determined by the ratio of the concentrations of the weak acid and weak base. As long as this ratio remains virtually constant, the $\mathrm{pH}$ will remain virtually constant. This will be the case as long as the concentrations of the buffering materials ($\chem{HA}$ and $\chem{A^–}$ or $\chem{B}$ and $\chem{BH^+}$) are large compared with amounts of $\chem{H^+}$ or $\chem{OH^–}$ added.

Buffering Capacity

The amount of protons or hydroxide ions the buffer can absorb without a significant change in pH.
Determined by the magnitudes of $\conc{HA}$ and $\conc{A^-}$.
A buffer with large capacity contains large concentrations of the buffering components.
Optimal buffering occurs when $\conc{HA}$ is equal to $\conc{A^-}$.
It is for this condition that the ratio $\frac{\conc{A^-}}{\conc{HA}}$ is most resistant to change when $\chem{H^+}$ or $\chem{OH^–}$ is added to the buffered solution.

Choosing a Buffer

$\mathrm{p}K_a$ of the weak acid to be used in the buffer should be as close as possible to the desired $\mathrm{pH}$.

Titration Curve

Plotting the $\mathrm{pH}$ of the solution being analyzed as a function of the amount of titrant added.
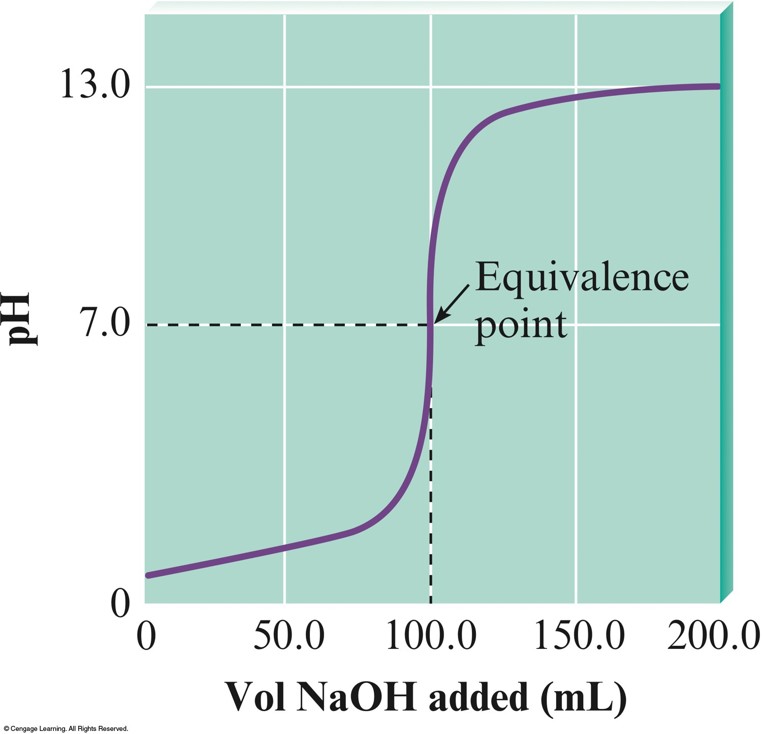
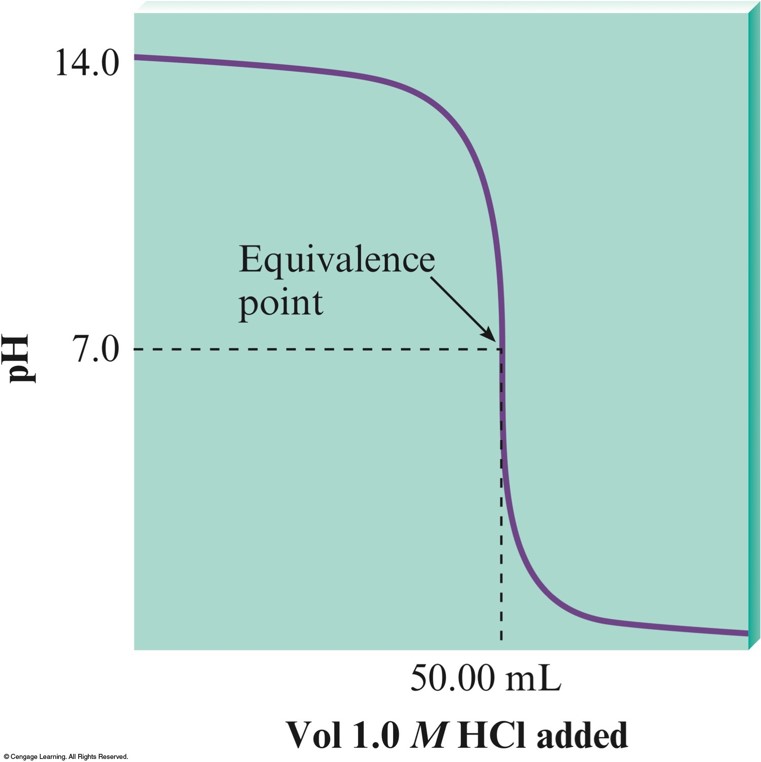
Equivalence (Stoichiometric) Point – point in the titration when enough titrant has been added to react exactly with the substance in solution being titrated.
When a strong acid and strong base are used, the equivalence point will be at a $\mathrm{pH}$ of 7.

The $\mathrm{pH}$ Curve for the Titration of $50.0\,\mathrm{mL}$ of $0.200\,\mathrm{M}\,\chem{HNO_3}$ with $0.100\,\mathrm{M}\,\chem{NaOH}$

The pH curve begins low (acidic) and then rises rapidly around the equivalence point (occuring at a pH of 7) and finally flattening out at a high pH as the base is added.

The $\mathrm{pH}$ Curve for the Titration of $100.0\,\mathrm{mL}$ of $0.50\,\mathrm{M}\,\chem{NaOH}$ with $1.0\,\mathrm{M}\,\chem{HCl}$

The pH curve begins high (basic) and then falls rapidly around the equivalence point (occuring at a pH of 7) and finally flattening out at a low pH as the acid is added.

Weak Acid-Strong Base Titration

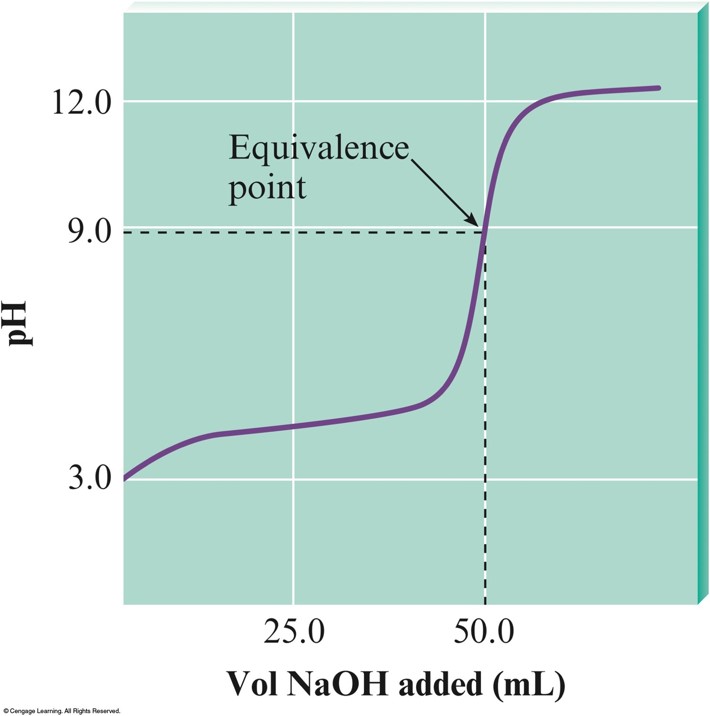
A stoichiometry problem (reaction is assumed to run to completion) then determine concentration of acid remaining and conjugate base formed.
An equilibrium problem (determine position of weak acid equilibrium and calculate $\mathrm{pH}$.

Concept Check

Calculate the $\mathrm{pH}$ of a solution made by mixing $0.20\,\mathrm{mol}\,\chem{HC_2H_3O_2}$ ($K_a=1.8 \times 10^{--5}$) with $0.030\,\mathrm{mol}\,\chem{NaOH}$ in $1.0\,\mathrm{L}$ of aqueous solution.

$\mathrm{pH}=3.99$

Exercise

Calculate the $\mathrm{pH}$ of a $100.0\,\mathrm{mL}$ solution of $0.100\,\mathrm{mol}\,\chem{HC_2H_3O_2}$, with $K_a=1.8 \times 10^{--5}$.

$\mathrm{pH}=2.87$

The $\mathrm{pH}$ Curve for the Titration of $50.0\,\mathrm{mL}$ of $0.100\,\mathrm{M}\,\chem{HC_2H_3O_2}$ with $0.100\,\mathrm{M}\,\chem{NaOH}$

The pH curve begins low, around 3, and then rises rapidly around the equivalence point (occuring at a pH of about 9) and finally flattening out at a high pH as the base is added.

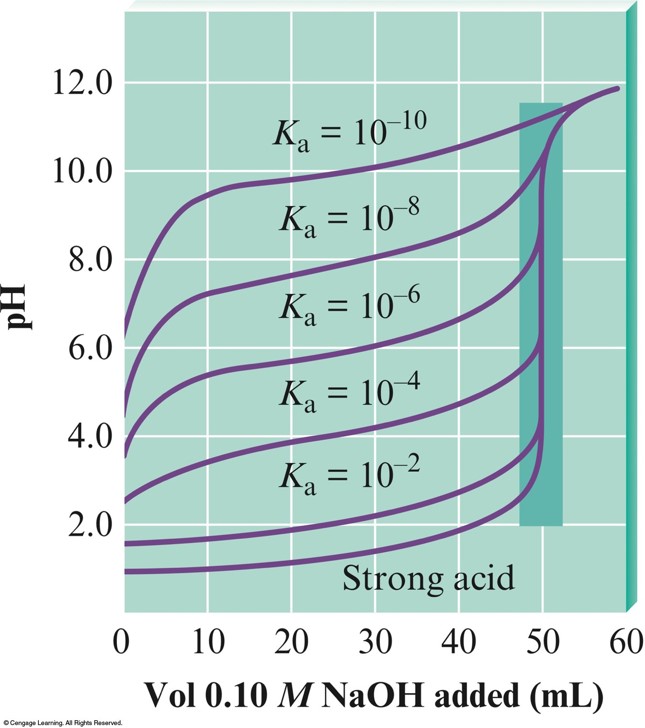
The $\mathrm{pH}$ Curves for the Titrations of $50.0-\mathrm{mL}$ Samples of $0.10\,\mathrm{M}$ Acids with Various $K_a$ Values with $0.10\,\mathrm{M}\,\chem{NaOH}$

The pH curve always begins low and transition to a higher pH. As the acid gets weaker, the initial pH of the curve gets higher.

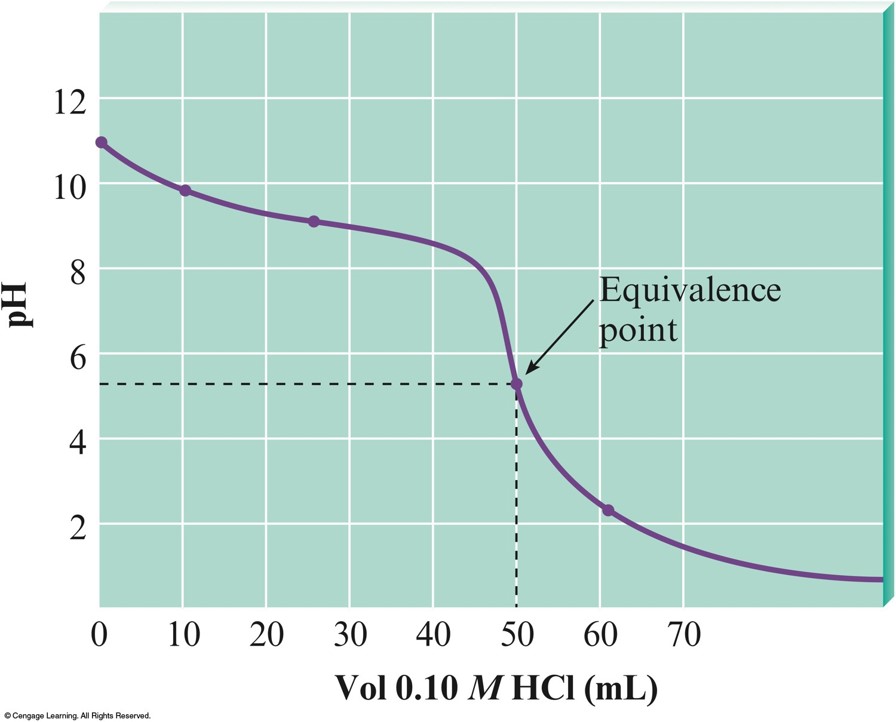
The $\mathrm{pH}$ Curve for the Titration of $100.0\,\mathrm{mL}$ of $0.050\,\mathrm{M}\,\chem{NH_3}$ with $0.10\,\mathrm{M}\,\chem{HCl}$

The pH curve begins high (basic) and then falls rapidly around the equivalence point (occuring at a pH of about 5) and finally flattening out at a low pH as the acid is added.

Acid-Base Indicators

Marks the end point of a titration by changing color.
The equivalence point is not necessarily the same as the end point (but they are ideally as close as possible).

The Acid and Base Forms of the Indicator Phenolphthalein

In an acidic solution, phenolphthalein is clear. In a basic solution, phenolphthalein is pink.

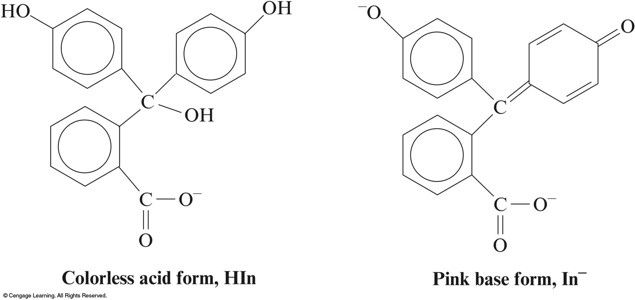
In its acidic form, phenolphthalein has three hydroxide groups whose hydrogens get removed when phenolphthalein is in a basic solution.

The Methyl Orange Indicator is Yellow in Basic Solution and Red in Acidic Solution

Methyl orange transitions from yellowish-orange in basic solutions to red in acidic solutions.

Useful $\mathrm{pH}$ Ranges for Several Common Indicators

The ranges at which a variety of indicator undergo their color change.

Property	Strong Acid	Weak Acid
\(K_a\) value	\(K_a\) is large	\(K_a\) is small
Position of the dissociation (ionization) equilibrium	Far to the right	Far to the left
Equilibrium concentration of \(\conc{H^+}\) compared with original	\(\conc{H^+}\approx \conc{HA}_0\)	\(\conc{H^+}\ll \conc{HA}_0\)
Strength of conjugate base compared with that of water	\(\chem{A^-}\) much weaker base than \(\chem{H_2O}\)	\(\chem{A^-}\) much stronger base than \(\chem{H_2O}\)

\(K_a>K_b\)	\(\mathrm{pH}<7\) (acidic)
\(K_b>K_a\)	\(\mathrm{pH}>7\) (basic)
\(K_a=K_b\)	\(\mathrm{pH}=7\) (neutral)

Acid	X	Electronegativity of X	\(K_a\) for Acid
\(\chem{HOCl}\)	\(\chem{Cl}\)	3.0	\( 4 \times 10^{-8} \)
\(\chem{HOBr}\)	\(\chem{Br}\)	2.8	\( 2 \times 10^{-9} \)
\(\chem{HOI}\)	\(\chem{I}\)	2.5	\( 2 \times 10^{-11} \)
\(\chem{HOCH_3}\)	\(\chem{CH_3}\)	2.3 (for carbon \(\chem{CH_3}\))	\( \sim 10^{-15} \)

Model	Definition of Acid	Definition of Base
Arrhenius	\(\chem{H^+}\) producer	\(\chem{OH^-}\) producer
Brønsted-Lowry	\(\chem{H^+}\) donor	\(\chem{H^+}\) acceptor
Lewis	Electron-pair acceptor	Electron-pair donor

Chapter 14 Acid-Base Equilibria

Models of Acids and Bases

Acid in Water

Acid Strength

Acid Strength

Various Ways to Describe Acid Strength

Water as an Acid and a Base

The pH Scale

The pH Scale and pH Values of Some Common Substances

Exercise

pH and pOH

Exercise

Exercise

Thinking About Acid-Base Problems

Concept Check

Concept Check

Solving Weak Acid Equilibrium Problems

Solving Weak Acid Equilibrium Problems (cont.)

Consider This

Exercise

Percent Dissociation (Ionization)

Exercise

Exercise

Bases

Concept Check

Concept Check

Weak Bases

Concept Check

Polyprotic Acids

Exercise

Concept Check

Salts

More of Salts

Summary of Properties of Salts

Qualitative Prediction of pH of Salt Solutions (from Weak Parents)

Exercise

Models of Acids and Bases

Oxyacids

Comparison of Electronegativitiy of X and \(K_a\) Value for a Series of Oxyacids

Oxides

Lewis Acids and Bases

Three Models for Acids and Bases

When analyzing an acid-base equilibrium problem:

Common Ion Effect

Key Points about Buffered Solutions

Solving Problems with Buffered Solution

Buffering: How Does It Work?

Henderson-Hasselbalch Equation

Exercise

Buffered Solution Characteristics

Buffering Capacity

Choosing a Buffer

Titration Curve

The \(\mathrm{pH}\) Curve for the Titration of \(50.0\,\mathrm{mL}\) of \(0.200\,\mathrm{M}\,\chem{HNO_3}\) with \(0.100\,\mathrm{M}\,\chem{NaOH}\)

The \(\mathrm{pH}\) Curve for the Titration of \(100.0\,\mathrm{mL}\) of \(0.50\,\mathrm{M}\,\chem{NaOH}\) with \(1.0\,\mathrm{M}\,\chem{HCl}\)

Weak Acid-Strong Base Titration

Concept Check

Exercise

The \(\mathrm{pH}\) Curve for the Titration of \(50.0\,\mathrm{mL}\) of \(0.100\,\mathrm{M}\,\chem{HC_2H_3O_2}\) with \(0.100\,\mathrm{M}\,\chem{NaOH}\)

The \(\mathrm{pH}\) Curves for the Titrations of \(50.0-\mathrm{mL}\) Samples of \(0.10\,\mathrm{M}\) Acids with Various \(K_a\) Values with \(0.10\,\mathrm{M}\,\chem{NaOH}\)

The \(\mathrm{pH}\) Curve for the Titration of \(100.0\,\mathrm{mL}\) of \(0.050\,\mathrm{M}\,\chem{NH_3}\) with \(0.10\,\mathrm{M}\,\chem{HCl}\)

Acid-Base Indicators

The Acid and Base Forms of the Indicator Phenolphthalein

The Methyl Orange Indicator is Yellow in Basic Solution and Red in Acidic Solution

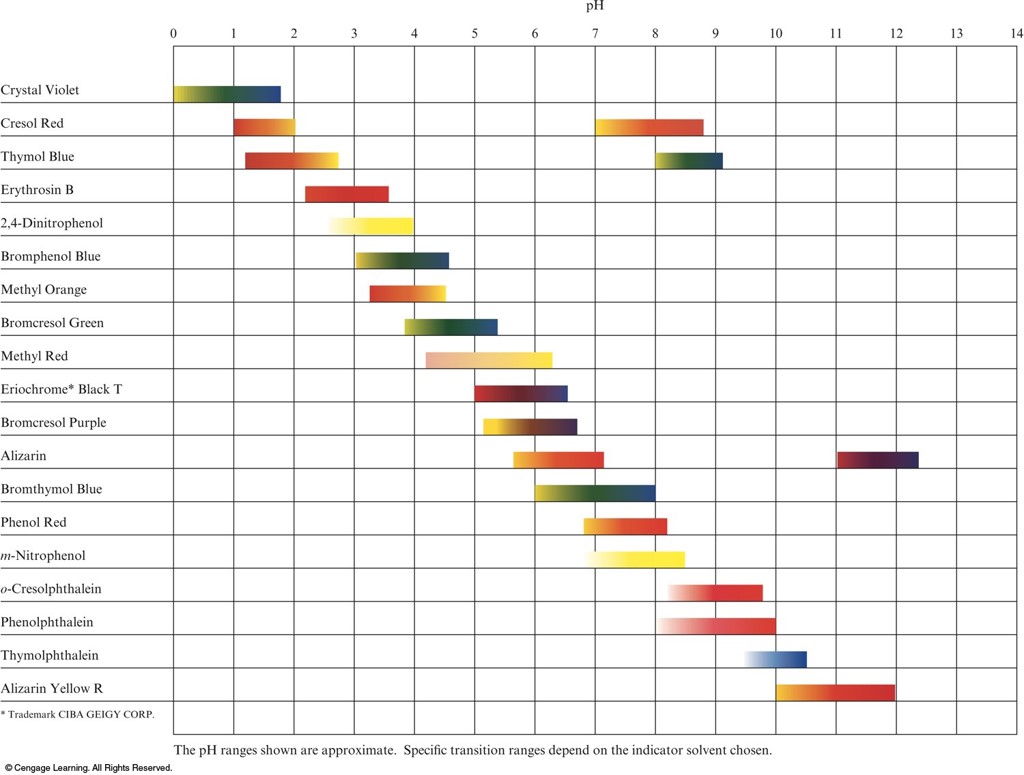
Useful \(\mathrm{pH}\) Ranges for Several Common Indicators

Chapter 14

Acid-Base Equilibria