Chapter 12

Kinetics

Shaun Williams, PhD

Chemical Equilibrium

• The state where the concentrations of all reactants and products remain constant with time.
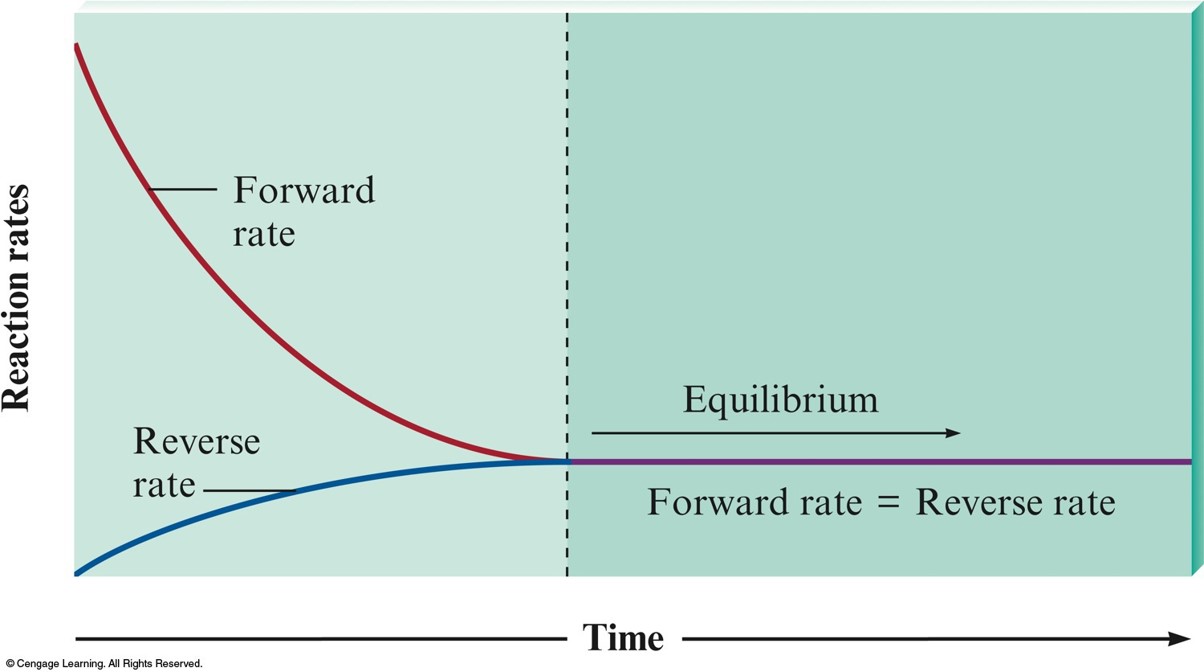
• On the molecular level, there is frantic activity. Equilibrium is not static, but is a highly dynamic situation.
• Equilibrium is:
• Macroscopically static
• Microscopically dynamic

The Changes with Time in the Rates of Forward and Reverse Reactions

Consider the following reaction at equilibrium

$$ j\chem{A}+k\chem{B}\rightleftharpoons l\chem{C}+m\chem{D} $$ $$ K=\frac{\conc{C}^l\conc{D}^m}{\conc{A}^j\conc{B}^k} $$

• \(\chem{A,\,B,\,C,\,D}\) - chemical species
• Square brackets - concentrations of species at equilibrium
• \(j,\,k,\,l,\,m\) - coefficients in the balanced equation
• \(K\) - equilibrium constant (given without units)

Conclusions About the Equilibrium Expression

• Equilibrium expression for a reaction is the reciprocal of that for the reaction written in reverse.
• When the balanced equation for a reaction is multiplied by a factor of \(n\), the equilibrium expression for the new reaction is the original expression raised to the nth power; thus \(K_\mathrm{new}=\left(K_\mathrm{original}\right)^n\).
• \(K\) values are usually written without units.
• \(K\) always has the same value at a given temperature regardless of the amounts of reactants or products that are present initially.
• For a reaction, at a given temperature, there are many equilibrium positions but only one equilibrium constant, \(K\).
• Equilibrium position is a set of equilibrium concentrations.

Example

$$\chem{N_2(g)+3H_2(g)\rightleftharpoons 2NH_3(s)} $$ $$ \begin{align} K &= \frac{\conc{NH_3}^2}{\conc{N_2}\conc{H_2}^3} \\ K_\mathrm{P} &= \frac{\left(P_\chem{NH_3}\right)^2}{\left(P_\chem{N_2}\right)\left(P_\chem{H_2}\right)^3} \end{align} $$

The Relationship Between \(K\) and \(K_\mathrm{P}\)

$$ K_\mathrm{P}=K\left(RT\right)^{\Delta n} $$

• \(\Delta n\) = sum of the coefficients of the gaseous products minus the sum of the coefficients of the gaseous reactants.
• \(R = 0.08206\,\bfrac{\mathrm{L\cdot atm}}{\mathrm{mol\cdot K}}\)
• \(T\) = temperature (in Kelvin)

Types of Equilibria

• Homogeneous equilibria - involve the same phase: $$ \chem{N_2(g)+3H_2(g) \rightleftharpoons 2NH_3(g)} $$ $$ \chem{HCN(aq) \rightleftharpoons H^+(aq) + CN^-(aq)} $$
• Heterogeneous equilibria – involve more than one phase: $$ \chem{2KClO_3(s) \rightleftharpoons 2KCl(s) + 3O_2(g)} $$ $$ \chem{2H_2O(l) \rightleftharpoons 2H_2(g) + O_2(g)} $$

Heterogeneous Equilibria

• The position of a heterogeneous equilibrium does not depend on the amounts of pure solids or liquids present.
• The concentrations of pure liquids and solids are constant.

The Extent of a Reaction

• A value of \(K\) much larger than 1 means that at equilibrium the reaction system will consist of mostly products – the equilibrium lies to the right.
• Reaction goes essentially to completion.
• A very small value of \(K\) means that the system at equilibrium will consist of mostly reactants – the equilibrium position is far to the left.
• Reaction does not occur to any significant extent.

Reaction Quotient, \(Q\)

• Used when all of the initial concentrations are nonzero
• Apply the law of mass action using initial concentrations instead of equilibrium concentrations.
• \(Q = K\): The system is at equilibrium. No shift will occur.
• \(Q > K\): The system shifts to the left.
• Consuming products and forming reactants, until equilibrium is achieved.
• \(Q < K\): The system shifts to the right.
• Consuming reactants and forming products, to attain equilibrium.

Set Up ICE Table

$$ \chem{Fe^{3+}(aq)+SCN^-(aq) \rightleftharpoons FeSCN^{2+}(aq)} $$ $$ \begin{align} & \chem{Fe^{3+}(aq)} & + & \chem{SCN^-(aq)} & \rightleftharpoons & \chem{FeSCN^{2+}(aq)} \\ \mathrm{Initial}\;\; & 6.00 & & 10.00 & & 0.00 \\ \mathrm{Change}\;\; & -4.00 & & -4.00 & & +4.00 \\ \mathrm{Equilibrium}\;\; & 2.00 & & 6.00 & & 4.00 \end{align} $$ $$ K=\frac{\conc{FeSCN^{2+}}}{\conc{Fe^{3+}}\conc{SCN^-}} = \frac{(4.00\,\mathrm{M})}{(2.00\,\mathrm{M})(6.00\,\mathrm{M})} = 0.333 $$

Solving Equilibrium Problems

1. Write the balanced equation for the reaction.
2. Write the equilibrium expression using the law of mass action.
3. List the initial concentrations.
4. Calculate \(Q\), and determine the direction of the shift to equilibrium.
5. Define the change needed to reach equilibrium, and define the equilibrium concentrations by applying the change to the initial concentrations.
6. Substitute the equilibrium concentrations into the equilibrium expression, and solve for the unknown.
7. Check your calculated equilibrium concentrations by making sure they give the correct value of \(K\).

Le Châtelier's Principle

• If a change is imposed on a system at equilibrium, the position of the equilibrium will shift in a direction that tends to reduce that change.
• Effects of Changes on the System
1. Concentration: The system will shift away from the added component. If a component is removed, the opposite effect occurs.
2. Temperature: \(K\) will change depending upon the temperature (endothermic – energy is a reactant; exothermic – energy is a product).
3. Pressure:
1. The system will shift away from the added gaseous component. If a component is removed, the opposite effect occurs.
2. Addition of inert gas does not affect the equilibrium position.
3. Decreasing the volume shifts the equilibrium toward the side with fewer moles of gas.