Chapter 11
Solutions and Colloids
Shaun Williams, PhD
Solution Composition
Various Types of Solutions
| Example | State of Solution | State of Solute | State of Solvent |
|---|---|---|---|
| Air, natural gas | Gas | Gas | Gas |
| Vodka, antifreeze | Liquid | Liquid | Liquid |
| Brass | Solid | Solid | Solid |
| Carbonated water | Liquid | Gas | Liquid |
| Seawater, sugar solution | Liquid | Solid | Liquid |
| Hydrogen in platinum | Solid | Gas | Solid |
Solution Composition
$$ \text{Molarity (M)} = \frac{\text{moles of solute}}{\text{liters of solution}} $$ $$ \text{Mass (weight) percent} = \frac{\text{mass of solute}}{\text{mass of solution}} \times 100\% $$ $$ \text{Mole fraction}\,(\chi_\text{A}) = \frac{\text{moles}_\text{A}}{\text{total moles of solution}} $$ $$ \text{Molality}\,(m) = \frac{\text{moles of solute}}{\text{kilogram of solvent}} $$
Exercise 1
You have 1.00 mol of sugar in 125.0 mL of solution. Calculate the concentration in units of molarity.
Exercise 1 - Answer
You have 1.00 mol of sugar in 125.0 mL of solution. Calculate the concentration in units of molarity.
$$ 8.00\,\text{M} $$
Exercise 2
You have a 10.0 M sugar solution. What volume of this solution do you need to have 2.00 mol of sugar?
Exercise 2 - Answer
You have a 10.0 M sugar solution. What volume of this solution do you need to have 2.00 mol of sugar?
$$ 0.200\,\text{L} $$
Exercise 3
A solution of phosphoric acid was made by dissolving 8.00 g of \(\chem{H_3PO_4}\) in 100.0 mL of water. Calculate the mole fraction of \(\chem{H_3PO_4}\). (Assume water has a density of 1.00 g/mL.)
Exercise 3 - Answer
A solution of phosphoric acid was made by dissolving 8.00 g of \(\chem{H_3PO_4}\) in 100.0 mL of water. Calculate the mole fraction of \(\chem{H_3PO_4}\). (Assume water has a density of 1.00 g/mL.)
$$ 0.0145 $$
Exercise 4
A solution of phosphoric acid was made by dissolving 8.00 g of \(\chem{H_3PO_4}\) in 100.0 mL of water. Calculate the molality of the solution. (Assume water has a density of 1.00 g/mL.)
Exercise 4 - Answer
A solution of phosphoric acid was made by dissolving 8.00 g of \(\chem{H_3PO_4}\) in 100.0 mL of water. Calculate the molality of the solution. (Assume water has a density of 1.00 g/mL.)
$$ 0.816\,\text{m} $$
The Energies of Solution Formation
Formation of a Liquid Solution
- Separating the solute into its individual components (expanding the solute).
- Overcoming intermolecular forces in the solvent to make room for the solute (expanding the solvent).
- Allowing the solute and solvent to interact to form the solution.
Steps in the Dissolving Process
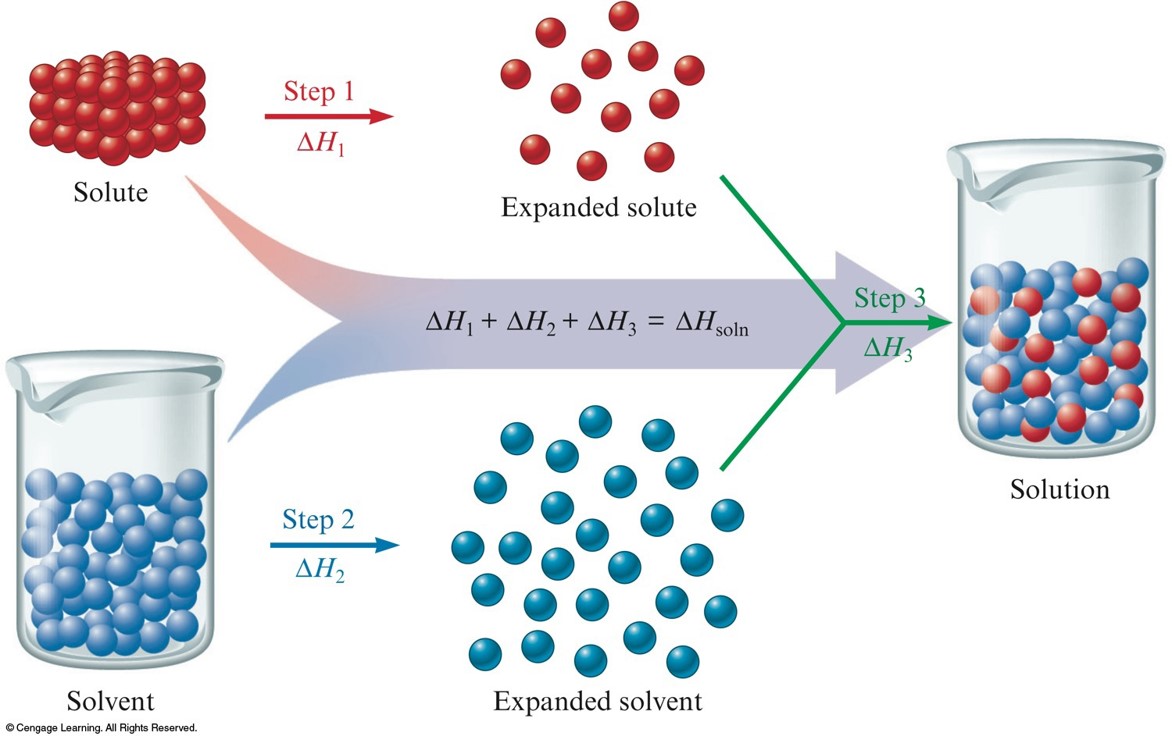
- Steps 1 and 2 require energy, since forces must be overcome to expand the solute and solvent.
- Step 3 usually releases energy.
- Steps 1 and 2 are endothermic, and step 3 is often exothermic.
Enthalpy (Heat) of Solution
- Enthalpy change associated with the formation of the solution is the sum of the ΔH values for the steps: $$ \Delta H_\text{soln} = \Delta H_1 + \Delta H_2 + \Delta H_3 $$
- \(\Delta H_\text{soln}\) may have a positive sign (energy absorbed) or a negative sign (energy released).
Enthalpy (Heat) of Solution
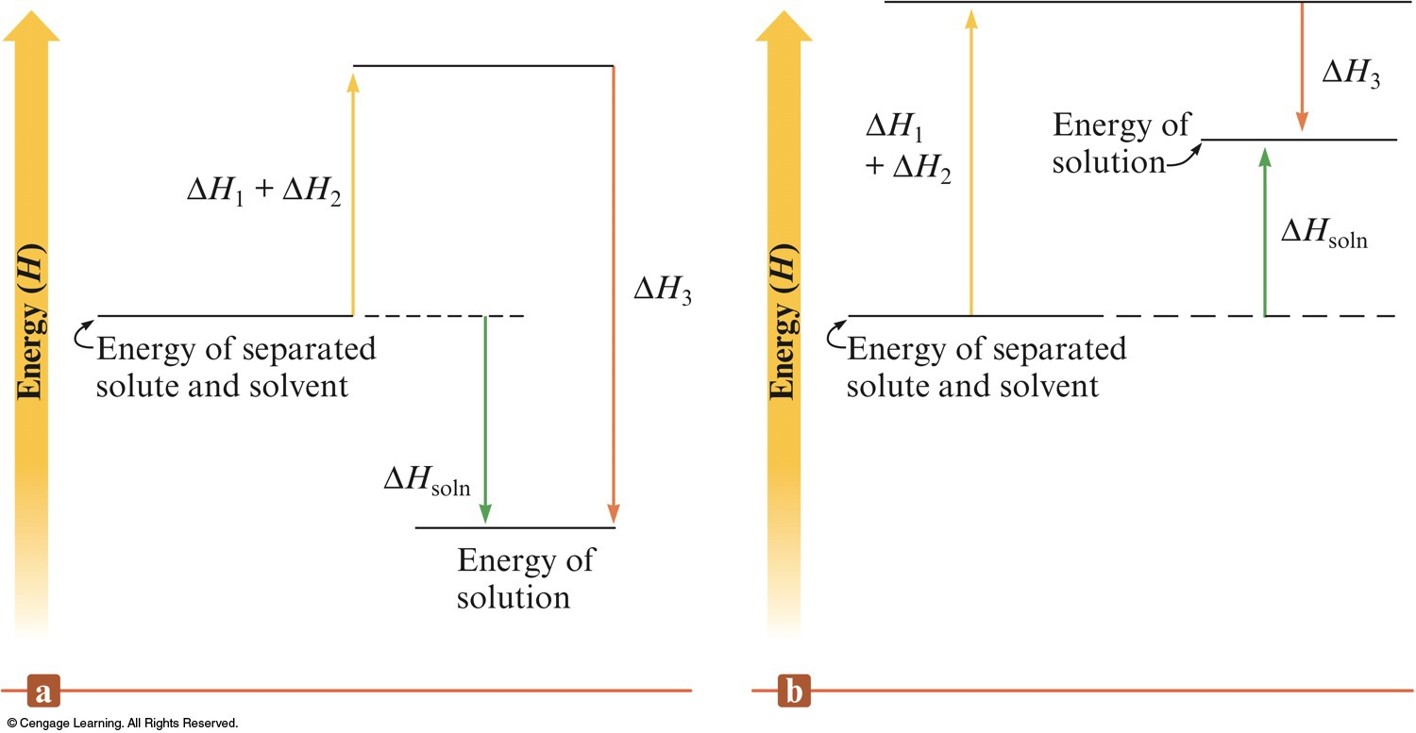
The Energy Terms for Various Types of Solutes and Solvents
| \(\Delta H_1\) | \(\Delta H_2\) | \(\Delta H_3\) | \(\Delta H_\text{soln}\) | Outcome | |
|---|---|---|---|---|---|
| Polar solute, polar solvent | Large | Large | Large, negative | Small | Solution forms |
| Nonpolar solute, polar solvent | Small | Large | Small | Large, positive | No solution forms |
| Nonpolar solute, nonpolar solvent | Small | Small | Small | Small | Solution forms |
| Polar solute, nonpolar solvent | Large | Small | Small | Large, positive | No solution forms |
In General
- One factor that favors a process is an increase in probability of the state when the solute and solvent are mixed.
- Processes that require large amounts of energy tend not to occur.
- Overall, remember that "like dissolves like".
Factors Affecting Solubility
- Structure Effects:
- Polarity
- Pressure Effects:
- Henry’s law
- Temperature Effects:
- Affecting aqueous solutions
Structure Effects
- Hydrophobic (water fearing)
- Non-polar substances
- Hydrophilic (water loving)
- Polar substances
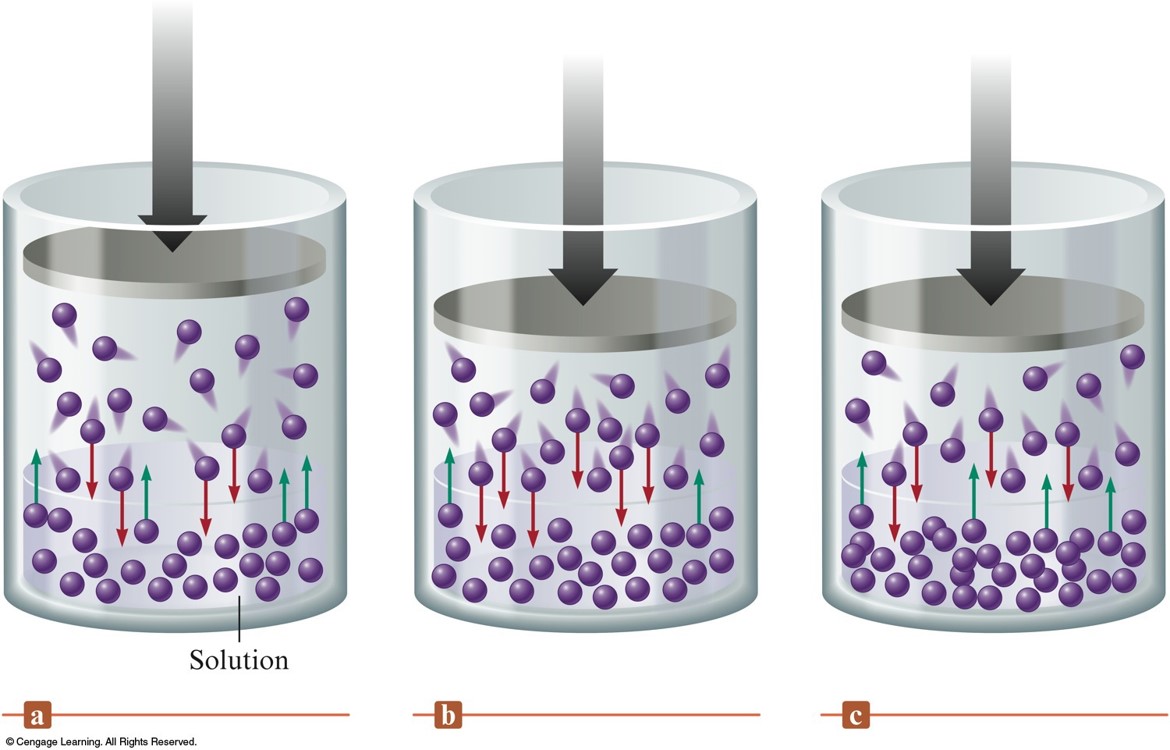
Pressure Effects
- Little effect on solubility of solids or liquids
- Henry’s law:
$$ C = kP $$
- \(C\) - concentration of dissolved gas
- \(k\) - constant
- \(P\) - partial pressure of gas solute above the solution
- Amount of gas dissolved in a solution is directly proportional to the pressure of the gas above the solution.
A Gaseous Solute
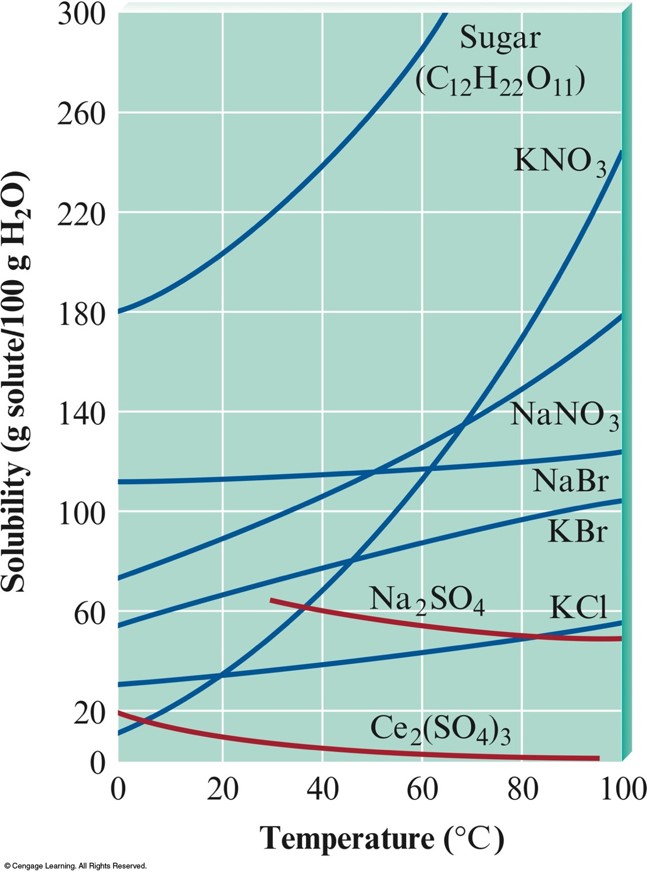
Temperature Effects (for Aqueous Solutions)
- Although the solubility of most solids in water increases with temperature, the solubilities of some substances decrease with increasing temperature.
- Predicting temperature dependence of solubility is very difficult.
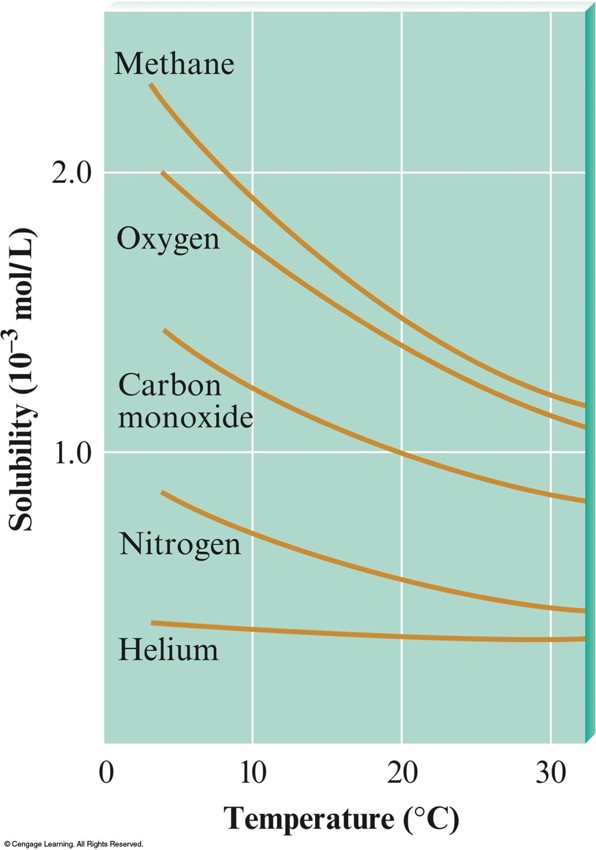
- Solubility of a gas in solvent typically decreases with increasing temperature.
The Solubilities of Several Solids as a Function of Temperature
The Solubilities of Several Gases in Water
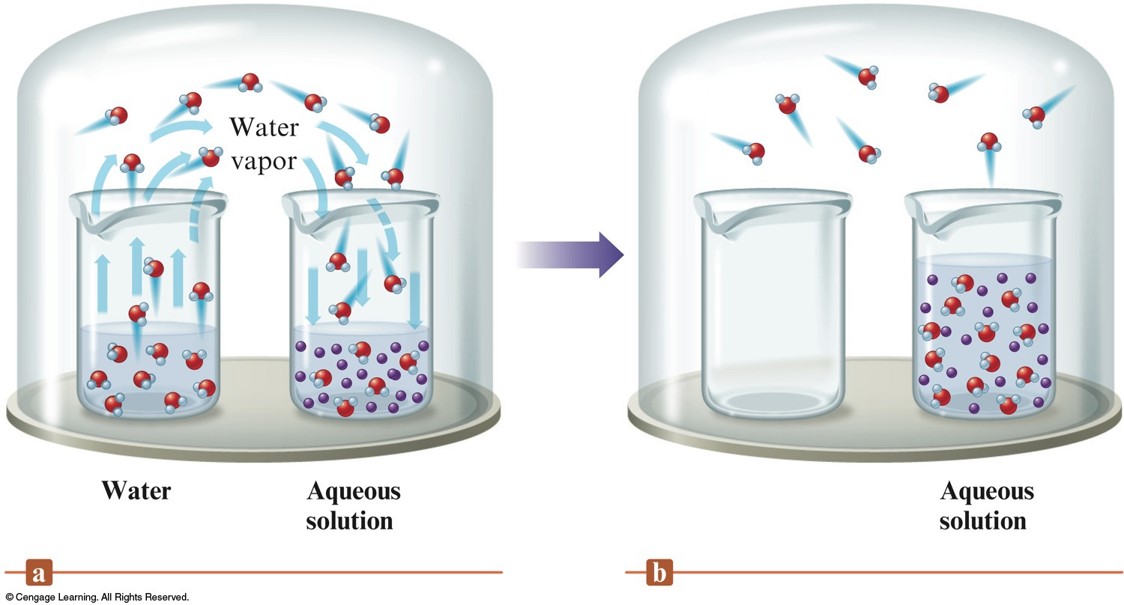
The Vapor Pressure of Solutions
An Aqueous Solution and Pure Water in a Closed Environment
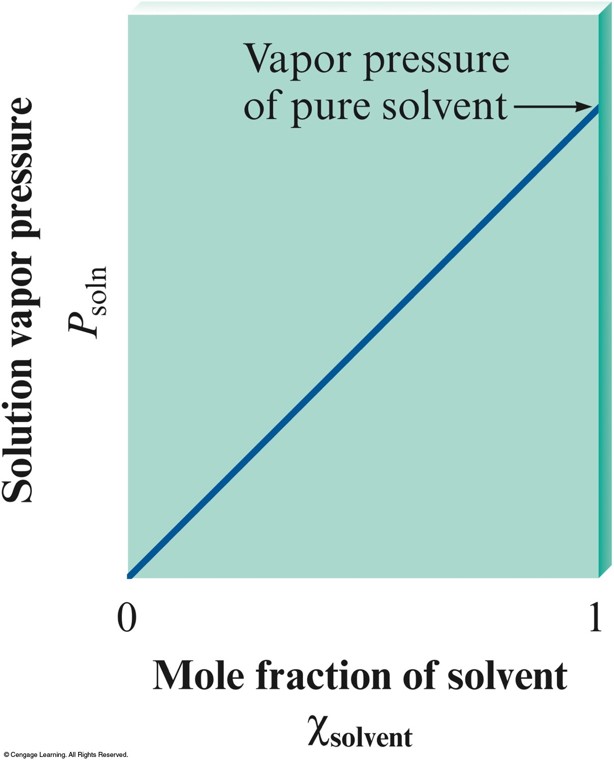
Vapor Pressures of Solutions
- Nonvolatile solute lowers the vapor pressure of a solvent.
- Raoult’s Law:
$$ P_\text{soln} = \chi_\text{solv} P_\text{solv}^\circ $$
- \(P_\text{soln}\) - observed vapor pressure of solution
- \(\chi_\text{solv}\) - mole fraction of solvent
- \(P_\text{solv}^\circ\) - vapor pressure of pure solvent
A Solution Obeying Raoult's Law
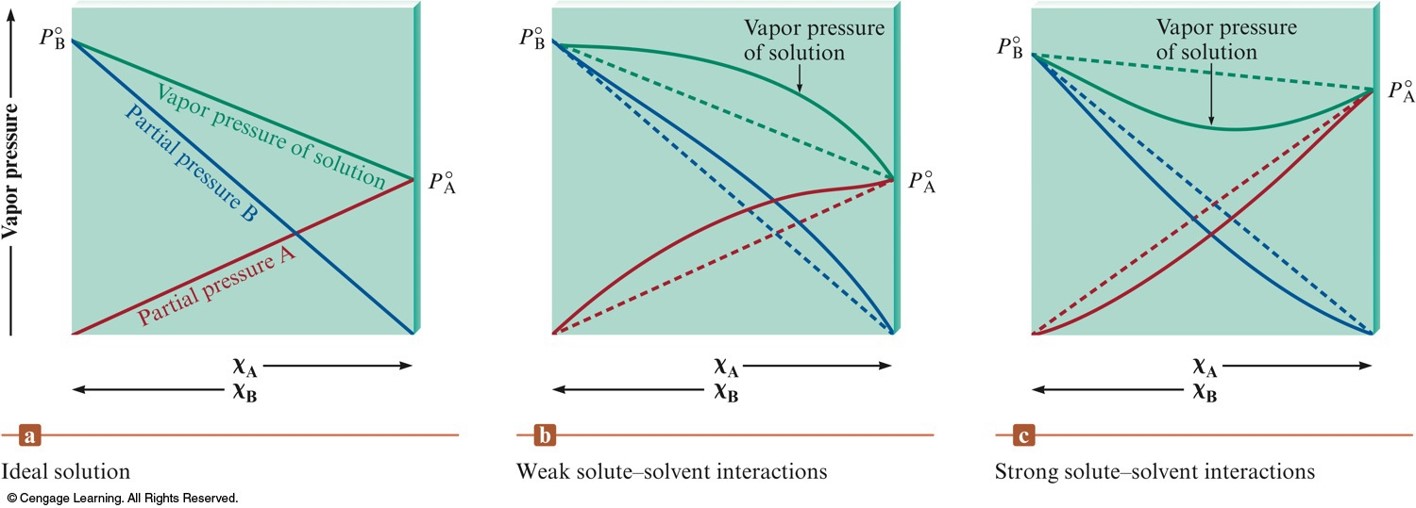
Nonideal Solutions
- Liquid-liquid solutions where both components are volatile.
- Modified Raoult’s Law: $$ P_\text{total} = \chi_\text{A} P_\text{A}^\circ + \chi_\text{B} P_\text{B}^\circ $$
- Nonideal solutions behave ideally as the mole fractions approach 0 and 1.
Vapor Pressure for a Solution of Two Volatile Liquids
Summary of the Behavior of Various Types of Solutions
| Interative Forces Between Solute (A) and Solvent (B) Particles | \(\Delta H_\text{soln}\) | \(\Delta T\) for Solution Formation | Deviation from Raoult's Law | Example |
|---|---|---|---|---|
| \(\chem{A\leftrightarrow A}, \chem{B\leftrightarrow B}\equiv \chem{A\leftrightarrow B}\) | Zero | Zero | None (ideal solution) | Benzene-toluene |
| \(\chem{A\leftrightarrow A}, \chem{B\leftrightarrow B} \lt \chem{A\leftrightarrow B}\) | Negative (exothermic) | Positive | Negative | Acetone-water |
| \(\chem{A\leftrightarrow A}, \chem{B\leftrightarrow B} \gt \chem{A\leftrightarrow B}\) | Positive (endothermic) | Negative | Positive | Ethanol-hexane |
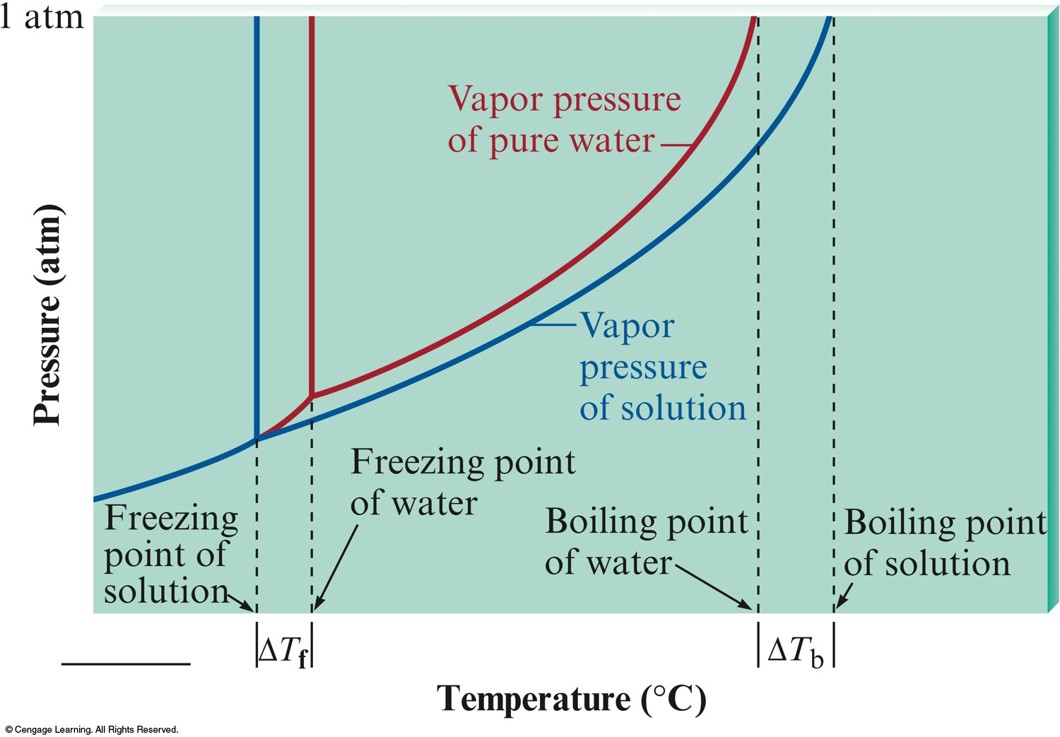
Boiling-Point Elevation and Freezing-Point Depression
Colligative Properties
- Depend only on the number, not on the identity, of the solute particles in an ideal solution:
- Boiling-point elevation
- Freezing-point depression
- Osmotic pressure
Boiling-Point Elevation
- Nonvolatile solute elevates the boiling point of the solvent.
- \(\Delta T = K_bm_\text{solute}\)
- \(\Delta T\) - boiling-point elevation
- \(K_b\) - molal boiling-point elevation constant
- \(m_\text{solute}\) - molality of solute
Freezing-Point Depression
- When a solute is dissolved in a solvent, the freezing point of the solution is lower than that of the pure solvent.
- \(\Delta T = K_fm_\text{solute}\)
- \(\Delta T\) - boiling-point elevation
- \(K_f\) - molal freezing-point depression constant
- \(m_\text{solute}\) - molality of solute
Changes in Boiling Point and Freezing Point of Water
Exercise 5
A solution was prepared by dissolving 25.00 g of glucose in 200.0 g water. The molar mass of glucose is 180.16 g/mol. What is the boiling point of the resulting solution (in °C)? Glucose is a molecular solid that is present as individual molecules in solution.
Exercise 5 - Answer
A solution was prepared by dissolving 25.00 g of glucose in 200.0 g water. The molar mass of glucose is 180.16 g/mol. What is the boiling point of the resulting solution (in °C)? Glucose is a molecular solid that is present as individual molecules in solution.
$$ 100.35^\circ \text{C} $$
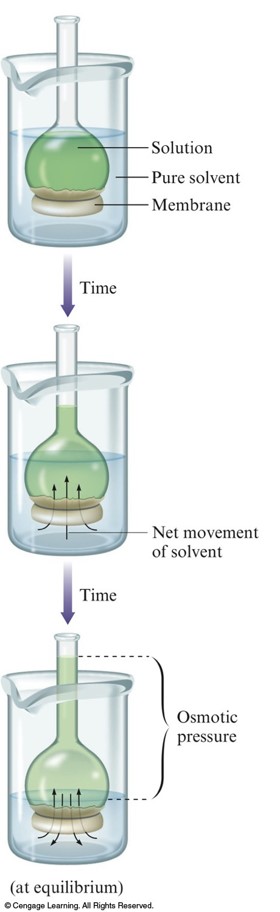
Osmotic Pressure
- Osmosis – flow of solvent into the solution through a semipermeable membrane.
- \( \Pi = MRT \)
- \(\Pi\) - osmotic pressure (atm)
- \(M\) - molarity of the solution
- \(R\) - gas law constant
- \(T\) - temperature (Kelvin)
Equilibrium in Osmosis System
Measuring Osmotic Pressure
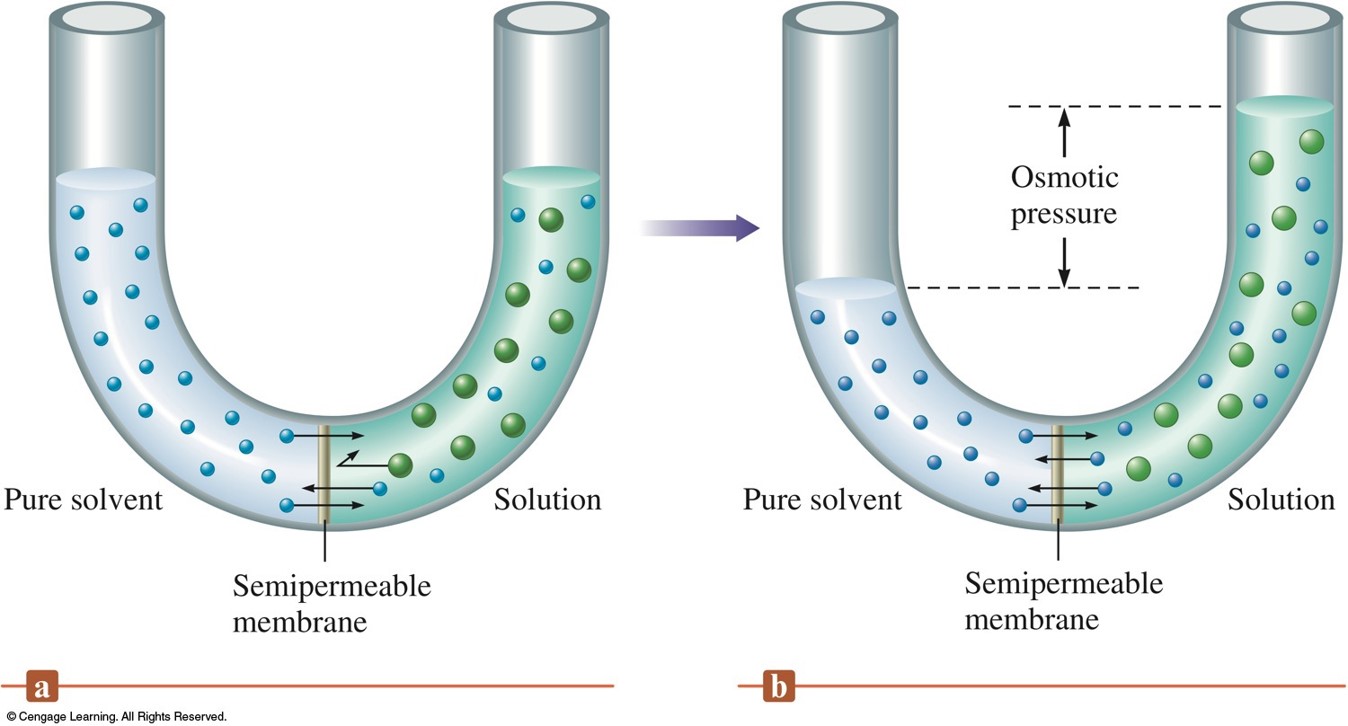
Exercise 6
When 33.4 mg of a compound is dissolved in 10.0 mL of water at 25°C, the solution has an osmotic pressure of 558 torr. Calculate the molar mass of this compound.
Exercise 6 - Answer
When 33.4 mg of a compound is dissolved in 10.0 mL of water at 25°C, the solution has an osmotic pressure of 558 torr. Calculate the molar mass of this compound.
$$ 111 \, \bfrac{\text{g}}{\text{mol}} $$
Colligative Properties of Electrolyte Solutions
van't Hoff Factor, \(i\)
- The relationship between the moles of solute dissolved and the moles of particles in solution is usually expressed as: $$ i=\frac{\text{moles of particles in solution}}{\text{moles of solute dissolved}} $$
- Modified equations $$ \Delta T = imK $$ $$ \Pi = iMRT $$
Examples
- The expected value for \(i\) can be determined for a salt by noting the number of ions per formula unit (assuming complete dissociation and that ion pairing does not occur).
- \(\chem{NaCl}\): \(i = 2\)
- \(\chem{KNO_3}\): \(i = 2\)
- \(\chem{Na_3PO_4}\): \(i = 4\)
Ion Pairing
- At a given instant a small percentage of the sodium and chloride ions are paired and thus count as a single particle.
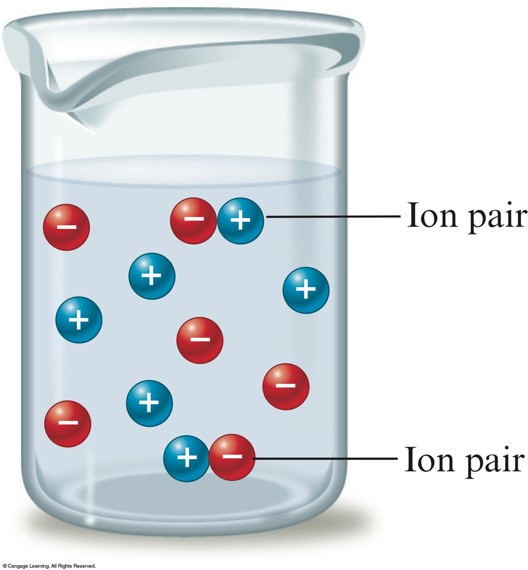
- Ion pairing is most important in concentrated solutions.
- As the solution becomes more dilute, the ions are farther apart and less ion pairing occurs.
- Ion pairing occurs to some extent in all electrolyte solutions.
- Ion pairing is most important for highly charged ions.
Colloids
- A suspension of tiny particles in some medium.
- Tyndall effect – scattering of light by particles.
- Suspended particles are single large molecules or aggregates of molecules or ions ranging in size from 1 to 1000 nm.
Types of Colloids
| Examples | Dispersing Medium | Dispersed Substance | Colloid Type |
|---|---|---|---|
| Fog, aerosol sprays | Gas | Liquid | Aerosol |
| Smoke, airborne bacteria | Gas | Solid | Aerosol |
| Whipped cream, soap suds | Liquid | Gas | Foam |
| Milk, mayonnaise | Liquid | Liquid | Emulsion |
| Paint, clays, gelatin | Liquid | Solid | Sol |
| Marshmallow, polystyrene foam | Solid | Gas | Solid foam |
| Butter, cheese | Solid | Liquid | Solid emulsion |
| Ruby glass | Solid | Solid | Solid sol |
Coagulation
- Destruction of a colloid.
- Usually accomplished either by heating or by adding an electrolyte.
/