Chapter 1

Essential Ideas

Shaun Williams, PhD

Chemistry: An Overview

Why chemistry seems hard

A main challenge of chemistry is to understand the connection between the macroscopic world that we experience and the microscopic world of atoms and molecules.
You must learn to think on the atomic level.

Atoms vs. Molecules

Matter is composed of tiny particles called atoms.
Atom: smallest part of an element that is still that element.
Molecule: Two or more atoms joined and acting as a unit.

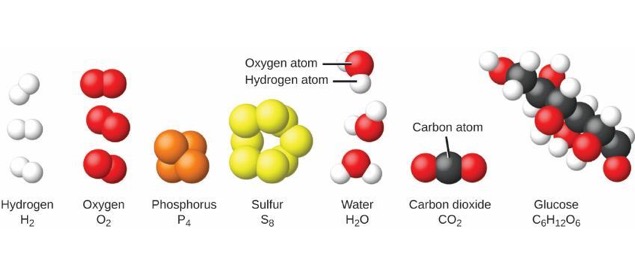
A single red sphere representing an oxygen atom. A single white sphere representing a hydrogen atom. Two white spheres connected to a red sphere representing a water molecule

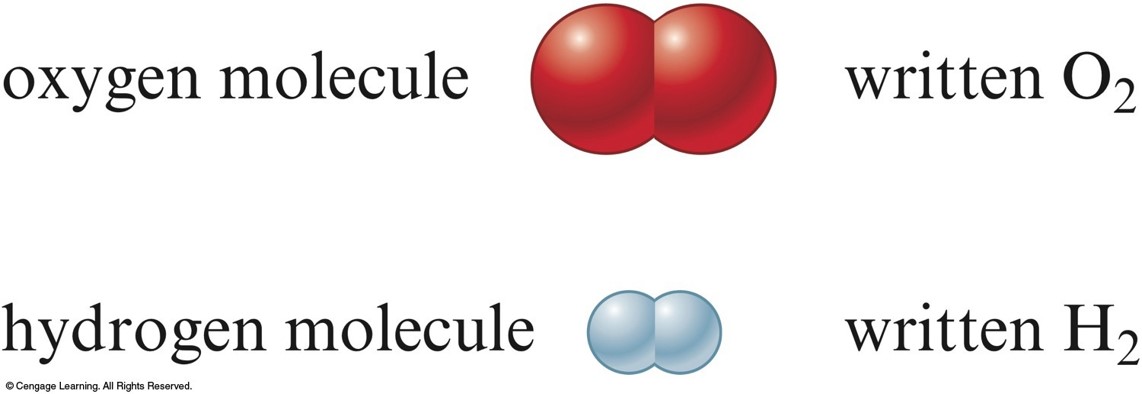
Oxygen and Hydrogen Molecules

Use subscripts when more than one atom is in the molecule.

Two oxygen atoms connected is the oxygen molecule, written O2. Two hydrogen atoms connected is the hydrogen molecule, written H2.

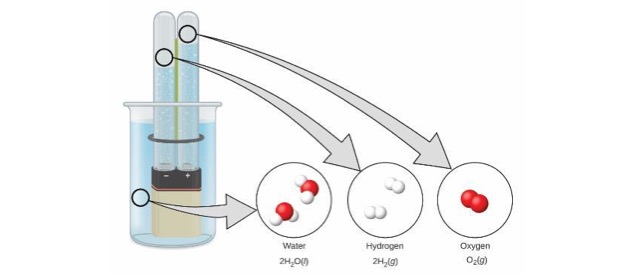
A Chemical Reaction

One substance changes to another by reorganizing the way the atoms are attached to each other.

Two water molecules can be split into one oxygen molecule and two hydrogen molecules by the application of an electric current.

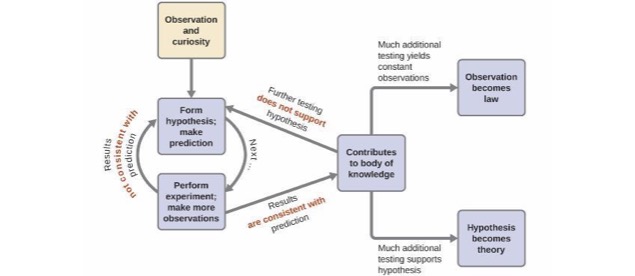
The Scientific Method

Science

Science is a framework for gaining and organizing knowledge.
Science is a plan of action — a procedure for processing and understanding certain types of information.
Scientists are always challenging our current beliefs about science, asking questions, and experimenting to gain new knowledge.
Scientific method is needed.

Fundamental Steps of the Scientific Method

Process that lies at the center of scientific inquiry.

A graphical representation of the scientific method.

Scientific Models

Law - A summary of repeatable observed (measurable) behavior.
Hypothesis - A possible explanation for an observation.
Theory (Model) - Set of tested hypotheses that gives an overall explanation of some natural phenomenon.

Units of Measurement

Nature of Measurement

Measurement

Quantitative observation consisting of two parts.
- number
- scale (unit)
Examples
- $20\, \chem{grams}$
- $ 6.63 \times 10^{-34}\,\chem{J}\cdot\chem{second}$

The Fundamental SI Units

Physical Quantity	Name of Unit	Abbreviation
Mass	kilogram	kg
Length	meter	m
Time	second	s
Temperature	kelvin	K
Electric current	ampere	A
Amount of substance	mole	mol
Luminous intensity	candela	cd

Prefixes Used in the SI System

Prefixes are used to change the size of the unit.

Prefix	Symbol	Meaning	Exponential Notation
exa	$\chem{E}$	$1,000,000,000,000,000,000$	$10^{18}$
peta	$\chem{P}$	$1,000,000,000,000,000$	$10^{15}$
tera	$\chem{T}$	$1,000,000,000,000$	$10^{12}$
giga	$\chem{G}$	$1,000,000,000$	$10^{9}$
mega	$\chem{M}$	$1,000,000$	$10^{6}$
kilo	$\chem{k}$	$1,000$	$10^3$
hecto	$\chem{h}$	$100$	$10^2$
deka	$\chem{da}$	$10$	$10^1$
-	$-$	$1$	$10^0$

More Prefixes Used in the SI System

Prefix	Symbol	Meaning	Exponential Notation
deci	$\chem{d}$	$0.1$	$10^{-1}$
centi	$\chem{c}$	$0.01$	$10^{-2}$
milli	$\chem{m}$	$0.001$	$10^{-3}$
micro	$\chem{\mu}$	$0.000001$	$10^{-6}$
nano	$\chem{n}$	$0.000000001$	$10^{-9}$
pico	$\chem{p}$	$0.000000000001$	$10^{-12}$
femto	$\chem{f}$	$0.00000000000001$	$10^{-15}$
atto	$\chem{a}$	$0.000000000000000001$	$10^{-18}$

Mass $\ne$ Weight

Mass is a measure of the resistance of an object to a change in its state of motion. Mass does not vary.
Weight is the force that gravity exerts on an object. Weight varies with the strength of the gravitational field.

Uncertainty in Measurement

Uncertainty in measurements

A digit that must be estimated in a measurement is called uncertain.
A measurement always has some degree of uncertainty. It is dependent on the precision of the measuring device.
Record the certain digits and the first uncertain digit (the estimated number).

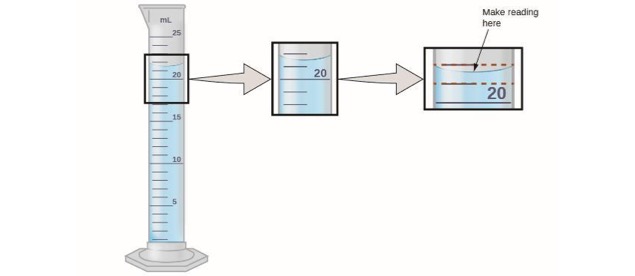
Measurement of Volume Using a Buret

The volume is read at the bottom of the liquid curve (meniscus).
Meniscus of the liquid occurs at about 20.15 mL.
- Certain digits: 20.15
- Uncertain digit: 20.15

A graphical representation of water in a buret.

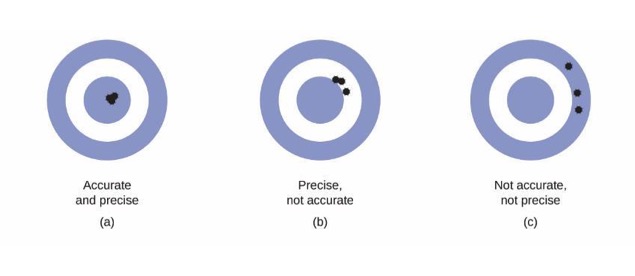
Precision and Accuracy

Accuracy - Agreement of a particular value with the true value.
Precision - Degree of agreement among several measurements of the same quantity.

Precision and Accuracy: Graphically

If all the darts on a dart board and randomly scattered you have an example of poor precision and poor accuracy. If all the darts miss the center but are all clustered together you have good precion but poor accuracy. If all the darts are clustered in the center you have good precision and good accuracy.

Significant Figures and Calculations

Rules for Counting Significant Figures

Underline the left-most, nonzero digit.
- $\underline{2}73.1023$
- $0.\underline{1}023$
- $0.\underline{7}10$
- $\underline{1}0.025$
- $\underline{1}020$

Rules for Counting Significant Figures (cont.)

We look to a decimal point.
1. If the number contains a decimal point, underline the right-most digit.
  - $\underline{2}73.102\underline{3}$
  - $0.\underline{1}02\underline{3}$
  - $0.\underline{7}1\underline{0}$
  - $\underline{1}0.02\underline{5}$
2. If the number does not contain a decimal point, underline the right-most, nonzero digit.
  - $\underline{1}0\underline{2}0$

Rules for Counting Significant Figures (concluded)

Count the numbers from one underlined number to the other.
- $\underline{2}73.102\underline{3}$ has 7 sig. figs.
- $0.\underline{1}02\underline{3}$ has 4 sig. figs.
- $0.\underline{7}1\underline{0}$ has 3 sig. figs.
- $\underline{1}0.02\underline{5}$ has 5 sig. figs.
- $\underline{1}0\underline{2}0$ has 3 sig. figs.

Special Types of Numbers

Exact numbers have an infinite number of significant figures.
- $1\,\chem{inch}=2.54\,\chem{cm}$, exactly (by definition).
- $9$ pencils (obtained by counting).

Exponential Notation

Example
- $300.$ written as $3.00 \times 10^2$
- Contains three significant figures.
Two Advantages
- Number of significant figures can be easily indicated.
- Fewer zeros are needed to write a very large or very small number.

Significant Figures in Mathematical Operations

For multiplication or division, the number of significant figures in the result is the same as the number in the least precise measurement used in the calculation. $$ 1.342 \times \underline{5.5} = 7.381 \xrightarrow{\chem{round}} \underline{7.4} $$
For addition or subtraction, the result has the same number of decimal places as the least precise measurement used in the calculation. $$ 23.445 + 7.8\underline{3} = 31.275 \xrightarrow{\chem{round}} 31.2\underline{8} $$

Dimensional Analysis

Converting between unit systems

Use when converting a given result from one system of units to another.
- To convert from one unit to another, use the equivalence statement that relates the two units.
- Derive the appropriate unit factor by looking at the direction of the required change (to cancel the unwanted units).
- Multiply the quantity to be converted by the unit factor to give the quantity with the desired units.

Example #1

A golfer putted a golf ball 6.8 ft across a green. How many inches does this represent?

To convert from one unit to another, use the equivalence statement that relates the two units. $$ 1\,\chem{ft} = 12\,\chem{in} $$ The two unit factors are: $$ \frac{1\,\chem{ft}}{12\,\chem{in}}\;\chem{and}\; \frac{12\,\chem{in}}{1\,\chem{ft}} $$

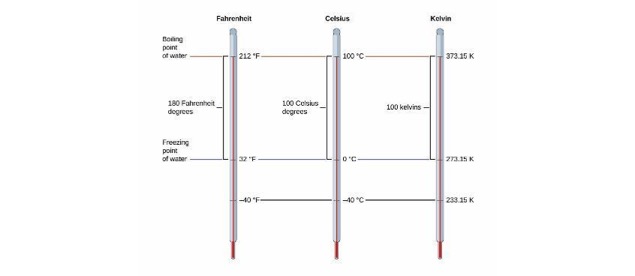
Temperature

Three Systems for Measuring Temperature

Fahrenheit
Celsius
Kelvin

Water freezes at 32 F, 0 C, and 273.15 K.

Density

Mass of substance per unit volume of the substance.
Common units are $\bfrac{\chem{g}}{\chem{cm^3}}$ or $\bfrac{\chem{g}}{\chem{mL}}$.

$$ \chem{Density}=\frac{\chem{mass}}{\chem{volume}} $$

Density Example 1

Calculate the density of a $ 0.03020\,L$ sample of ethanol with a mass of $ 23.71002\,g$.

Density Example 2

What is the volume of an object that has a density of $ 10.2\bfrac{g}{mL}$ and a mass of $ 30.0\,kg$?

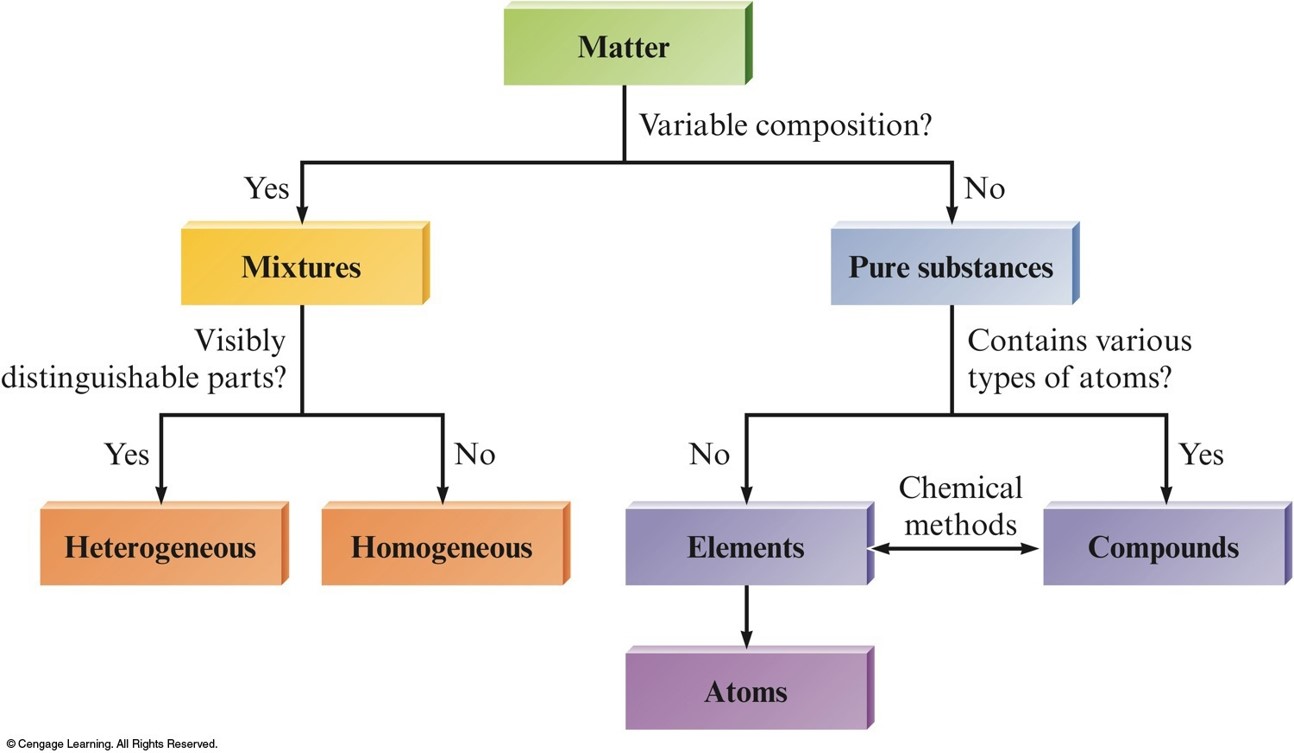
Classification of Matter

Matter

Anything occupying space and having mass.
Matter exists in three states.
- Solid
- Liquid
- Gas

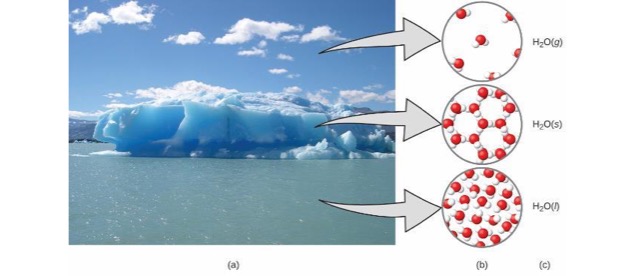
In solid water, the molecules are well order,stuck in place, and close together. In liquid water, the molecules are randomly arranges, moving a little, and still close together. In gaseous water, the molecules are randomly arranged, moving very rapidly, and far apart. These conditions are true for all molecules in these phases.

The Phases - Macroscopically

Solid
- Rigid
- Has fixed volume and shape.
Liquid
- Has definite volume but no specific shape.
- Assumes shape of container.
Gas
- Has no fixed volume or shape.
- Takes on the shape and volume of its container.

Mixtures

Have variable composition.

Homogeneous mixture - Having visibly indistinguishable parts; solution.
Heterogeneous mixture - Having visibly distinguishable parts.

Pure Substances

Have a single composition.

Element - A pure substance that cannot be broken down using chemical reactions.
Compound - A pure substance that can be broken down using chemical reactions.

Physical Change

Change in the form of a substance, not in its chemical composition.
- Example: boiling or freezing water
Can be used to separate a mixture into pure compounds, but it will not break compounds into elements.
- Distillation
- Filtration
- Chromatography

Chemical Change

A given substance becomes a new substance or substances with different properties and different composition.
- Example: Bunsen burner (methane reacts with oxygen to form carbon dioxide and water)

Concept Check!

Which of the following are examples of a chemical change?

Pulverizing (crushing) rock salt
Burning of wood
Dissolving of sugar in water
Melting a popsicle on a warm summer day

Concept Check! Answer