Chemical Kinetics: Elementary Reactions

Shaun Williams, PhD

Reaction Rates

Reaction Rate

• Chemical kinetics is the study of chemical reaction rates.
• In order to understand kinetics, there are some background equations that we need.
• These equations will be fully developed later in the course.

The Collision Frequency

• \( \gamma = \rho \sigma \left< v_{AA} \right> \)
• The effective cross-sectional area of the colliding molecules is $$ \sigma_{AB}=\frac{1}{4}\left( \sigma_A + 2\sqrt{\sigma_A \sigma_B} +\sigma_B \right) $$
• The average relative speed is $$ \left< v_{AB} \right> = \sqrt{\frac{8k_\mathrm{B}T}{\pi \mu}} $$
• The reduced mass is \( \mu = \frac{m_A m_B}{m_A+m_B} \)

Fick's First Law

• Some reaction rates are limited by diffusion
• In these cases, we will use Fick's first law to help quantify the dynamics.
• \( J(Z_0) = -D\left. \left( \frac{d\rho}{dZ} \right) \right|_{Z_0} \)

Equilibrium Constant

• The equilibrium constant can be written in terms of partition function (a lot more on that later in the course) $$ K_{\mathrm{eq}} = \frac{Q_{\mathrm{products}}}{Q_{\mathrm{reactants}}} $$
• We can also write it in terms of the standard state Gibbs' Free energy \( \Delta_{\mathrm{rxn}} G^\ominus \) $$ K_\mathrm{eq} = e^{-\frac{\Delta_\mathrm{rxn}G^\ominus}{RT}} $$
• The Gibbs' Free energy can be broken down as \( \Delta G = \Delta H - T \Delta S \)
• The enthalpy for any process is given as \( H = E + PV \)

Reaction Rates

• Chemical kinetics is the study of chemical reaction rates.
• In kinetics, both microscopic and macroscopic parameters of the system are crucial to understanding chemical behavior

Microscopic Parameter: Orientation of Reactants

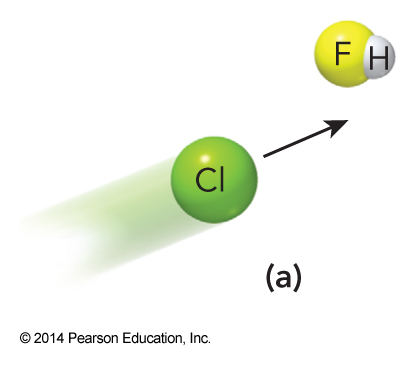
• Consider the reaction $$ \mathrm{Cl(g) + HF(g) \rightarrow HCl(g) + F(g)} $$
• For this reaction $$ \Delta_\mathrm{rxn}H^\ominus = 165.198+173.779-186.908-158.754 = -6.685\,\frac{kJ}{mol} $$
• This reaction is less probable if the chlorine attacks from the F end of the HF molecule.
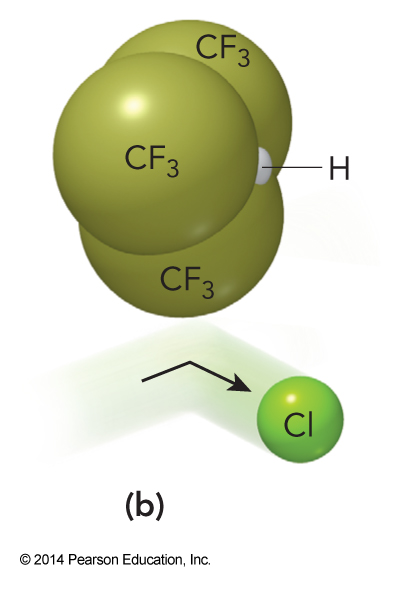
• This reaction is even less probable if the fluorine atom is replaced wiht much larger functional groups. $$ \mathrm{Cl(g) + (CF_3)_3CH(g) \rightarrow HCl(g) + (CF_3)_3C(g)} $$
• Because of these steric considerations we should expect that the first reaction will be much more probable than the second reaction
• This means that we should expect the reaction rate of the first reaction to be faster than the reaction rate of the second reaction.

Diagrams of the Importance of the Orientation of Reactants

Microscopic Parameter: Energy Barrier to Reaction

• During a chemical reaction, the potential energy of the system tends to increase.
• The total energy of the system, however, is constant.
• Basically, the reacting system is exchanging kinetic energy (vibrational and rotational) for potential energy.
• A chemical reaction must overcome the activation energy in order to react.
• The activation energy is the peak in potential energy between the reactants and products.
• The height of this barrier depends on the molecular structure and quantum mechanics.

Macroscopic Parameters

• The rate at which we observe changes in a system depends on the system's thermodynamic parameters.

Concentrations

• The language of chemical kinetics grew out of the study of reactions in solutions.
• We tend to represent the amount of each molecule in formulas using molarity.
• Even in gas phase reactions we describe the concentration using the number density is particles per \( \mathrm{cm}^{-3} \)

Temperature

• The rate constant is a function of temperature (we will later determine this dependence)

Reaction Velocities

• We can define a reaction velocity as $$ v=\frac{1}{\nu_i}\frac{d\left[ i \right]}{dt} = \frac{1}{V\nu_i}\frac{dn_i}{dt} $$
• \( \left[ i \right] \) - molar concentation of product or reactant \( i \)
• \( \nu_i \) - the stoichiometric coefficient of \( i \) in the reaction
• \( n_i \) - the number of moles of component \( i \) contained in volume \( V \)
• The use of the stoiciometric coefficient in the equation is to ensure that the same reaction rate is found regardless of what component is being considered.
• For the reaction \( \mathrm{2H_2 + O_2 \rightarrow 2H_2O} \) $$ -\frac{1}{2}\frac{d\left[ \mathrm{H_2}\right]}{dt} = -\frac{d\left[ \mathrm{O_2}\right]}{dt} = \frac{1}{2}\frac{d\left[ \mathrm{H_2O}\right]}{dt} $$

Rate Laws and Complications

• Often, the reaction velocity is written in terms of a rate law
• The rate law is a power law in the reactant concentrations
• The rate law includes a concentration-independent coefficient called the rate constant, \(k \)
• An example of a generic rate law $$ v=k\left[ A\right]^x\left[ B\right]^y\dots $$
• The reaction order is the sum of the exponents, \( x+y+\dots \)

Elementary vs Net Reactions

• A net rreaction is a reaction written to show only the initial and final chemical components, for example $$ \mathrm{2H_2 + O_2 \rightarrow 2H_2O} $$
• This reaction actually occurs in a series of steps $$ \begin{align} \mathrm{H_2 + O_2} & \rightarrow \mathrm{H+HO_2} \\ \mathrm{HO_2 + H_2} & \rightarrow \mathrm{H_2O + OH} \\ \mathrm{H + OH + M} & \rightarrow \mathrm{H_2O + M} \end{align} $$ The \( M \) in the last step is shorthand for any particle that participates in the reaction without being changed
• Each of these individual steps is called an elementary step.
• Elementary steps require only a single collision or decay.

Reaction Mechanisms

• The reaction mechanism is the series of elementary reaction that lead to a net reaction equation
• On the previous slide, if we add up the three elementary steps, we get the net equation
• In this chapter we will focus on elementary reactions

Types of Elementary Reactions: Unimolecular

• If the initial reactant is unstable $$ \mathrm{XeCl \rightarrow Xe + Cl} $$
• If the reactant molecule has been previous energized (through collisions or laser) $$ \mathrm{C_2H_4O_2\,(dioxetane) \rightarrow 2H_2CO} $$

Types of Elementary Reactions: Bimolecular and Termolecular

• A bimolecular elementary reaction involves the collision between two reactants $$ \mathrm{Cl + HCl \rightarrow Cl_2 + H} $$
• A termolecular elementary reaction involves the collision between three reactants $$ \mathrm{He + H + Cl \rightarrow He + HCl} $$
• It is important to note that the probability of three reactants colliding simultaneously is very small compared to bimolecular collisions
• Elementary reactions involving more than three reactants have not been found.

Simple Collision Theory

Simple Collision Theory

• We now what to fold together the parameters to predict the value of the rate constant, \( k \)
• For our simplest model of chemical reactions, we fix the temperature and assume the following
1. The reaction is bimolecular, \( \mathrm{A + B} \xrightarrow{k} \mathrm{products} \)
2. The reactants must be close enough for intermolecular forces to be important before the reaction can take place.
3. A single distribution function describes the probability of the reaction occuring
4. There will be some activation barrier to overcome

Derivation Summary: Simple Collision Theory

• First we count the number of collisions per unit time
• Multiply that by the fraction of those collision with enough kinetic energy
• this bring in the canonical factor \( e^{-\frac{E_a}{RT}} \) (later in the course)
• Bringing all this together we arrive at a version of the empirical Arrhenius equation $$ k_\mathrm{Arr}=Ae^{-\frac{E_a}{RT}} $$ namely $$ k_\mathrm{SCT} = \sigma_\mathrm{AB} \sqrt{\frac{8k_\mathrm{B}T}{\pi \mu}} \mathcal{N}_\mathrm{A} p e^{-\frac{E_a}{RT}} $$ where \( p \) is a steric factor.

Behavior of the Arrhenius Rate Constant

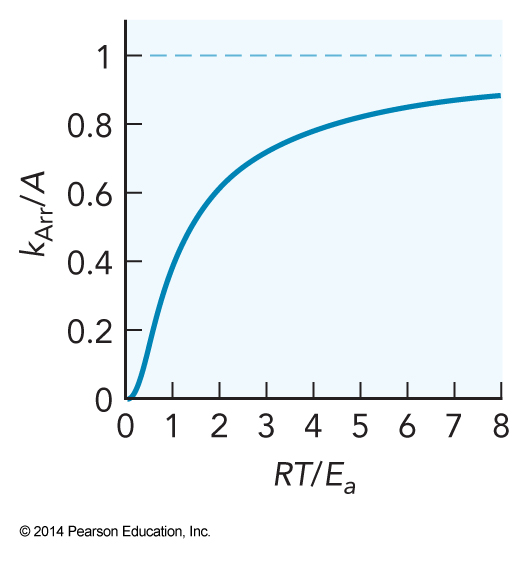
• Note: When \( RT=E_a \), \( k_\mathrm{Arr} \) is about at one-third of its maximum value.

Example 13.1

Estimate the value of \( A \) in \( \mathrm{cm^3\,mol^{-1}\,s^{-1}} \) for the reaction between oxygen atom and molecular nitrogen, \( \mathrm{O(g) + N_2(g)} \), at \( 298\,\mathrm{K} \). Let the collision cross-section be \( 30\, \AA^2 \) for oxygen and \( 37\, \AA^2 \) for \( \mathrm{N_2} \).

Using the Arrhenius Equation

• We would like to be able to measure the value of \( k \) at various temperatures in the lab and determine the value of \( E_a \)
• To do this, we first need to rearrange the Arrhenius equation

$$ \begin{align} k & = A \exp \left( -\frac{E_a}{RT} \right) \\ \frac{k}{A} & = \exp \left( -\frac{E_a}{RT} \right) \\ \ln \frac{k}{A} & = -\frac{E_a}{RT} \end{align} $$

First of Two Results in the Derivation

$$ \begin{align} \frac{d}{dT} \left( \ln \frac{k}{A} \right) & = -\frac{d}{dT} \frac{E_a}{RT} \\ \frac{d}{dT} \left( \ln k - \ln A \right) & = \frac{d}{dT} \ln k = -\left( -\frac{E_a}{RT^2} \right) = \frac{E_a}{RT^2} \\ E_a & \equiv RT^2 \frac{d\ln k}{dT} \end{align} $$ This result is great, but experimentally, we needs a more useful approach.

First of Two Results in the Derivation

Let's try a more useful approach $$ \begin{align} \ln \frac{k}{A} & = -\frac{E_a}{RT} \\ \ln k - \ln A & = -\frac{E_a}{RT} \\ \ln k & = -\frac{E_a}{R}\frac{1}{T} + \ln A \end{align} $$ This is now linear. A plot of \( \ln k \) versus \( \frac{1}{T} \) will provide a straight line with a slope of \( -\frac{E_a}{R} \) and a y-intercept of \( \ln A \).

The Arrhenius Plot

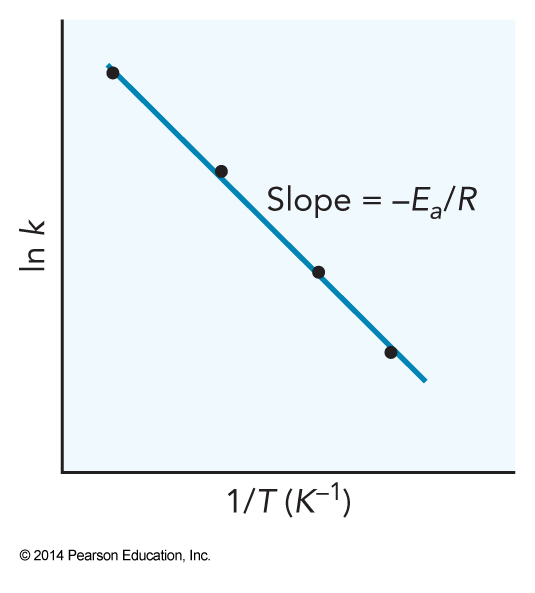
Example 13.2

For the reaction \( 2NOBr \rightarrow 2NO + Br_2 \), calculate \( k \) at \( 298\,\mathrm{K} \) assuming only the Arrhenius equation (constants given in Table 13.1 of the book). Then predict the values of \( k \) at \( 400\,\mathrm{K} \) if (a) the Arrhenius equation continues to hold and (b) if the Arrhenius value at \( 298\,\mathrm{K} \) is correct but \( A \) is actually of the form \( A' T^\frac{1}{2} \).

Transition State Theory

Transition State Theory

• Many kinetic models take advantage of transition state theory or activated complex theory
• This theory describes a chemical reaction as a process in which reactants combine to form an activated complex which then decays to product $$ \mathrm{A+B \rightarrow AB^\ddagger \rightarrow products} $$

Reaction Diagram for Bimolecular Transition State Theory

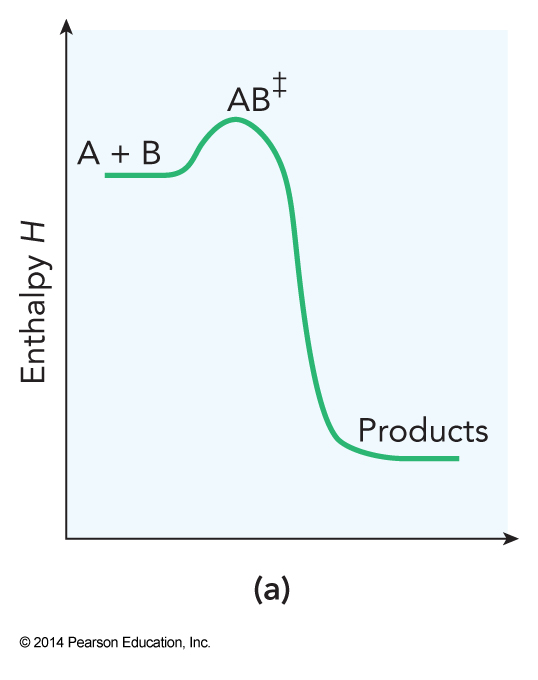
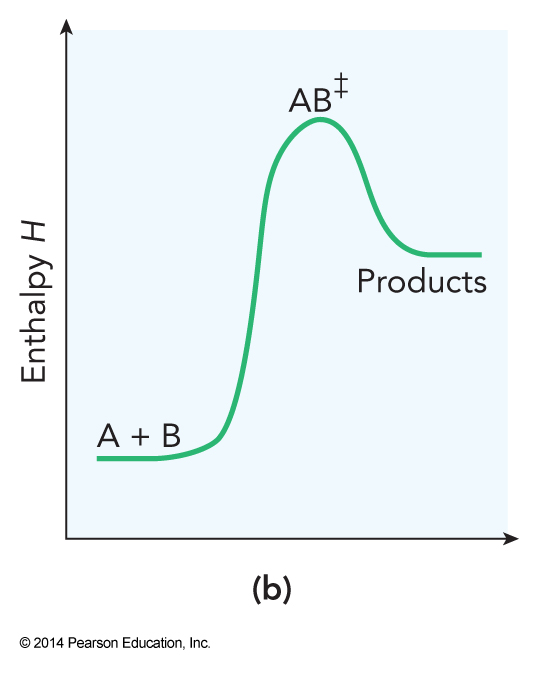
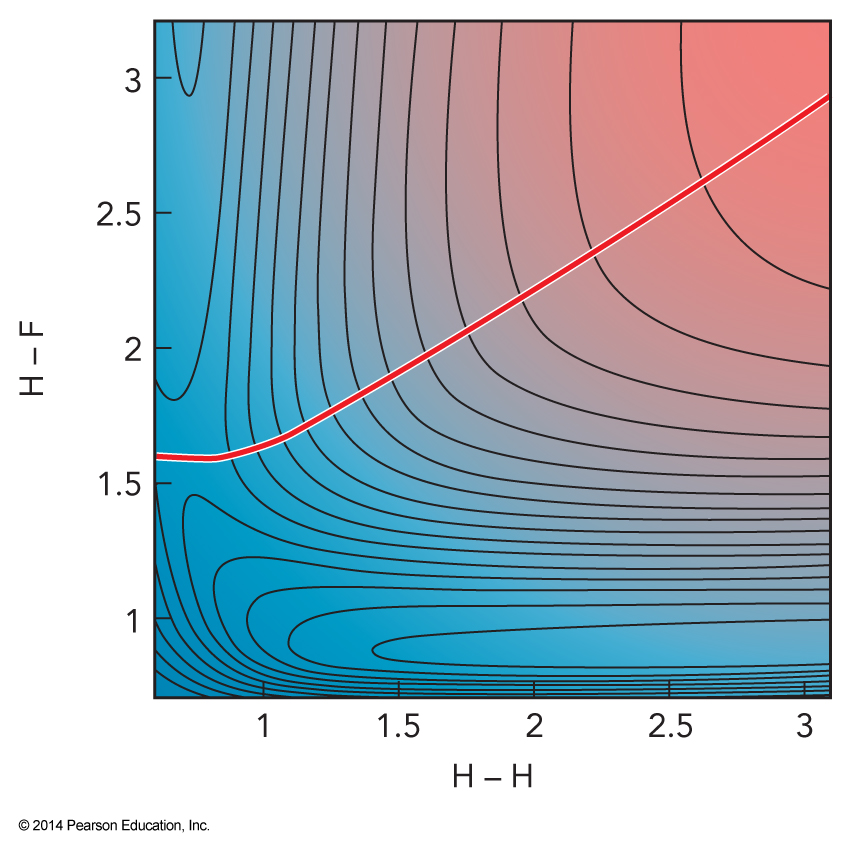
Dividing Surface for \( \mathrm{H+HF} \)

Eyring Equation

• The rate constant equation that we get utilizing transition state theory is called the Eyring equation $$ k_\mathrm{TST} = \frac{k_\mathrm{B}T}{Ch}\exp \left( \frac{\Delta S^\ddagger}{R} \right) \exp \left( -\frac{\Delta H^\ddagger}{RT} \right) $$ where \( C \) is the overall concentration
• Here we have a slightly more complex version than Arrhenius involving more thermodynamic quantities
• Our steric factor has been replaced by a term dependent on the entropy change which makes sense

Diffusion-Limited Rate Constants

Diffusion-Limited Rate Constants

• Our equations thus far have only taken into account gas phase diffusion
• In order to correctly model reactions in solutions we need to allow for the diffusion of the reactants in a solvent
• We are going to use Fick's first law to do this $$ J=-D\left( \frac{d\rho}{dZ} \right) $$ where \( J \) is the diffusion-limited flux of molecules per unit area per unit time

Diffusion-Limited Reaction

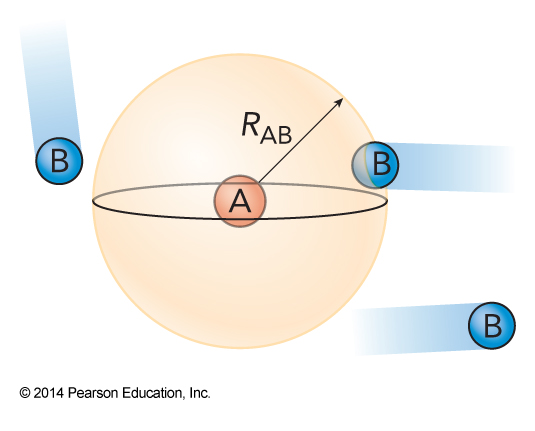
• To estimate the diffusion-limited rate constant, we assume a sphere centered on each molecule A such that any molecule B that gets inside the sphere will react.

Diffusion Rate

• The rate, in molecules per unit time, of B diffusing into any sphere of radius \( r \) is given the symbol \( \gamma_\mathrm{D} \) $$ \begin{align} \gamma_\mathrm{D} & = -J_\mathrm{B} \left( 4\pi r^2 \right) \\ & = D_\mathrm{AB} \left( 4\pi r^2 \right) \left( \frac{d\rho_\mathrm{B}}{dr} \right) \end{align} $$
• Doing some math we arrive at $$ \gamma_\mathrm{D} = 4\pi R_\mathrm{AB} D_\mathrm{AB} \rho_\mathrm{B} $$

Diffusion-Limited Rate Constant

• Using our diffusion rate equation we can derive a rate constant
• This rate constant assumes:
1. Diffusion-limited rate
2. A bimolecular reaction
• The diffusion-limited rate constant is $$ k_\mathrm{D}=4\pi R_\mathrm{AB} D_\mathrm{AB} $$

Rate Laws for Elementary Reactions

Rate Law for Elementary Reactions

• Both simple collision and transition state theories find that the reaction rate depends solely on the rate constant and the concentrations of the reactants $$ \mathrm{elementary\, reaction:}\, v=k\prod_\mathrm{reactants} \left[ \mathrm{i} \right]^{v_\mathrm{i}} $$
• Some examples: $$ \begin{align} \mathrm{A \rightarrow products:}\; & v=k\left[ \mathrm{A} \right] \\ \mathrm{A + B \rightarrow products:}\; & v=k\left[ \mathrm{A} \right] \left[ \mathrm{B} \right] \\ \mathrm{2A \rightarrow products:}\; & v=k\left[ \mathrm{A} \right]^2 \\ \mathrm{A + B + C \rightarrow products:}\; & v=k\left[ \mathrm{A} \right] \left[ \mathrm{B} \right] \left[ \mathrm{C} \right] \\ \end{align} $$

Unimolecular Decomposition

• Let's look at a generic unimolecular decomposition reaction, \( A \rightarrow B + C \)
• The rate law for this reaction is $$ v = \frac{d\left[\mathrm{B}\right]}{dt} = -\frac{d\left[\mathrm{A}\right]}{dt} = k\left[\mathrm{A}\right] $$
• We would like to come up with an equation that allows us to determine the concentration of a species as a function of time
• To do this, we need to do a little math

First Order Integrated Rate Law

• Starting with \( -\frac{d\left[\mathrm{A}\right]}{dt} = k\left[\mathrm{A}\right] \) we find that: $$ \begin{align} -\frac{d\left[\mathrm{A}\right]}{\left[\mathrm{A}\right]} & = k\, dt \\ -\int_{\left[\mathrm{A}\right]_0}^{\left[\mathrm{A}\right]} \frac{d\left[\mathrm{A}\right]'}{\left[\mathrm{A}\right]'} & = k\int_0^t dt \\ -\ln \frac{\left[\mathrm{A}\right]}{\left[\mathrm{A}\right]_0} & = kt \; \therefore \; \left[\mathrm{A}\right] = \left[\mathrm{A}\right]_0 e^{-kt} \\ \mathrm{if\, \left[B\right]_0 = \left[C\right]_0 = 0:}\; \left[\mathrm{B}\right] & = \left[\mathrm{C}\right] = \left[\mathrm{A}\right]_0\left(1-e^{-kt}\right) \end{align} $$

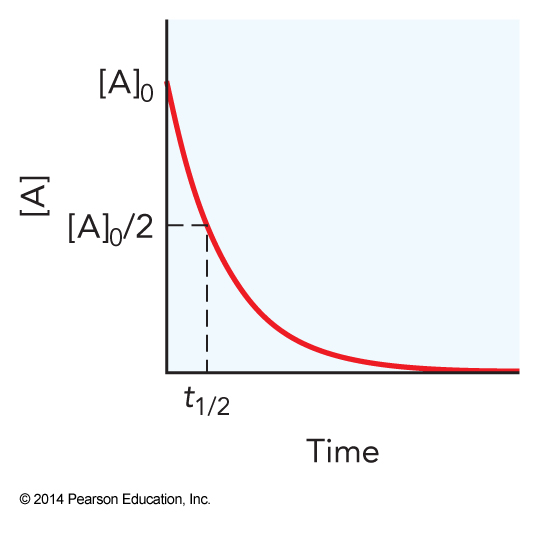
Reaction Half-Life

• Once we have the integrated rate law we can determine the reaction half-life
• The half-life, \( t_\bfrac{1}{2} \), is the time is takes the reaction for \( \left[\mathrm{A}\right] = \frac{1}{2}\left[\mathrm{A}\right]_0 \)
• So $$ \begin{align} -\ln \frac{\left[\mathrm{A}\right]}{\left[\mathrm{A}\right]_0} & = kt \\ -\ln \frac{\frac{1}{2}\left[\mathrm{A}\right]_0}{\left[\mathrm{A}\right]_0} & = kt_\bfrac{1}{2} \\ -\ln \frac{1}{2} & = kt_\bfrac{1}{2} \; \therefore \; t_\bfrac{1}{2} = -\frac{1}{k}\ln \frac{1}{2} = \frac{\ln 2}{k} \end{align} $$

Concentration Versus Time

Example 13.3

Find the integrated rate law for the elementary reaction \( \mathrm{2A\rightarrow B} \), where \( \mathrm{A} \) is butadiene and \( \mathrm{B} \) is vinylcyclohexene. Use this to obtain an expression for the half-life of butadiene in terms of the rate constant \( k \) and the initial concentration \( \left[ \mathrm{A} \right]_0 \).