The Second and Third Laws: Entropy
Shaun Williams, PhD
Entropy of a Dilute Gas
Entropy of a Dilute Gas
- We are going to calculate the total entropy of a gas
- Assume: constant energy and volume
- Assume: gas is dilute – ignore intermolecular forces
- Our gas molecules will be able to rotate and vibrate
- We will skip the derivation however and show the results
Ensemble Size of the 3D Box System
- Using geometry and calculus we can arrive at an expression of the ensemble size of gas in a 3D box $$ \Omega = \frac{1}{N!\left[\left(\frac{3N}{2}\right)-1\right]!}\left(\frac{\pi}{4}\right)\left(\frac{2\pi mEV^\bfrac{2}{3}}{h^2}\right)^{\left(\frac{3N}{2}\right)-1} $$
- This means that the size of the ensemble becomes huge as \(m\), \(E\), and \(V\) approach bulk.
Example Ensemble Sizes

Entropy
- We can use Boltzmann’s equation to determine the entropy based on our ensemble size $$ \begin{align} S &= k_\mathrm{B}\ln \Omega \\ &= k_\mathrm{B} \ln \left[ \frac{1}{N!\left[\frac{3N}{2}-1\right]!} \frac{\pi}{4} \left( \frac{2\pi mEV^\bfrac{2}{3}}{h^2} \right)^{\frac{3N}{2}-1} \right] \\ &= k_\mathrm{B}\left[ \begin{split} & -\ln N! - \ln \left(\frac{3N}{2}-1\right)! + \ln \left(\frac{\pi}{4}\right) \\ & + \left(\frac{3N}{2}-1\right) \ln \left(\frac{2\pi mEV^\bfrac{2}{3}}{h^2}\right) \end{split} \right] \end{align} $$
- Using Stirling's approximation $$ S = k_\mathrm{B}\left\{ \begin{split} & -N\ln N + N - \left(\frac{3N}{2}-1\right) \ln \left(\frac{3N}{2}-1\right) + \left(\frac{3N}{2}-1\right) \\ & + \ln \left(\frac{\pi}{4}\right) + \left(\frac{3N}{2}-1\right) \ln \left(\frac{2\pi mEV^\bfrac{2}{3}}{h^2}\right) \end{split} \right\} $$
Continuing the Derivation
$$ \begin{align} S &= k_\mathrm{B}\left\{ \begin{split} & -N\ln N + N - \left(\frac{3N}{2}-1\right) \ln \left(\frac{3N}{2}-1\right) \\ & + \left(\frac{3N}{2}-1\right) + \ln \left(\frac{\pi}{4}\right) \\ & + \left(\frac{3N}{2}-1\right) \ln \left(\frac{2\pi mEV^\bfrac{2}{3}}{h^2}\right) \end{split} \right\} \\ &\approx k_\mathrm{B} \left\{ \begin{split} & -N\ln N + N - \left(\frac{3N}{2}\right) \ln \left(\frac{3N}{2}\right) + \left(\frac{3N}{2}\right) \\ & + \ln \left(\frac{\pi}{4}\right) + \left(\frac{3N}{2}\right) \ln \left(\frac{2\pi mEV^\bfrac{2}{3}}{h^2}\right) \end{split} \right\} \\ \end{align} $$
Still More Derivation
$$ \begin{align} S &\approx k_\mathrm{B} \left\{ \begin{split} & -N\ln N + N - \left(\frac{3N}{2}\right) \ln \left(\frac{3N}{2}\right) + \left(\frac{3N}{2}\right) \\ & + \ln \left(\frac{\pi}{4}\right) + \left(\frac{3N}{2}\right) \ln \left(\frac{2\pi mEV^\bfrac{2}{3}}{h^2}\right) \end{split} \right\} \\ &= k_\mathrm{B} \left\{ N\left[ -\ln N + 1 - \frac{3}{2}\ln \frac{3N}{2} + \frac{3}{2} + \frac{3}{2} \ln \left(\frac{2\pi mEV^\bfrac{2}{3}}{h^2}\right) \right] \right\} \\ &= Nk_\mathrm{B} \left\{ \frac{5}{2} -\ln N +\ln\left(\frac{2}{3N}\right)^\bfrac{3}{2} + \ln \left(\frac{2\pi mEV^\bfrac{2}{3}}{h^2}\right)^\bfrac{3}{2} \right\} \\ &= Nk_\mathrm{B} \left\{ \frac{5}{2} + \ln \left[ \left(\frac{4\pi mE}{3Nh^2}\right)^\bfrac{3}{2} \frac{V}{N} \right] \right\} \end{align} $$
Sackur-Tetrode Equation
- If we set \(N\) equal to \(\mathcal{N}_\mathrm{A}\) we will get the molar entropy
- Note that \(R=\mathcal{N}_\mathrm{A}\)
- The Sackur-Tetrode equation deals only with translational degrees of freedom.
- It is limited to monatomic gases
- We will return to consider the rotational and vibrational contributions to entropy later.
The Second Law of Thermodynamics
Return to an Example
- A system is equally likely to be found in any of the available microstates at any time
- Going back to an expanding gas under a piston
- Let’s consider the gas as many particles in a 3D box – expands in one dimension
- The initial volume is \(2.445\,\mathrm{L}\) and the total energy is fixed
- Many quantum states are consistant
Total Number of Microstates
- Starting with a previous equation $$ \begin{align} \Omega &= \frac{1}{N!\left[\left(\frac{3N}{2}\right)-1\right]!} \left(\frac{\pi}{4}\right)\left(\frac{2\pi mEV^\bfrac{2}{3}}{h^2}\right)^{\frac{3N}{2}-1} \\ \Omega(E,V,N) &= \frac{1}{N!\left[\left(\frac{3N}{2}\right)-1\right]!} \left(\frac{2\pi mE}{4\pi^2\hbar^2}\right)^{\frac{3N}{2}-1} \frac{\pi}{4V^\bfrac{2}{3}}V^N \end{align} $$
- Simplifying with a fixed, large number of moles $$ \left(\frac{\partial \Omega}{\partial V}\right)_{E,N} \approx \frac{1}{N!\left[\left(\frac{3N}{2}\right)-1\right]!} \left(\frac{2\pi mE}{4\pi^2\hbar^2}\right)^{\frac{3N}{2}-1} \frac{\pi}{4V^\bfrac{2}{3}}NV^{N-1} $$
Increasing Volume
- What happens when our volume increases?
- If our volume increases by \(\frac{dV}{V}=10^{-10}\) $$ \frac{d\Omega}{\Omega} = N\frac{dV}{V} = \left(6.02\times 10^{23}\right)\left(10^{-10}\right)=6.02\times 10^{13} $$
- So, the chance our system will be found in a larger volume than its initial volume is immensely greater
- The number of microstates has increased immensely
Meaning
- Say that the sample changes quantum states each time two molecules collide, \(\sim 10^{30}\) times per sec.
- The probability at each of these collisions that the system will remain at the original volume is one in \(6.02\times 10^{13}\).
- This means that the sample will expand immediately
- When possible, systems always move to a greater number of quantum states (greater entropy)
Second Law of Thermodynamics
- The second law of thermodynamics can be stated as:
- For any process in a system totally isolated from its surroundings, the macroscopic entropy measured over the entire system \(S_T\) can never decrease: \(\Delta S_T \ge 0\)
- Qualifiers
- The entropy can decrease in a process, but only in a local region or (for a microscopic system) over a short time
- If we allow the system to communicate with its surroundings, the entropy change in the system could decrease, but it would have to be matched by an increase in the entropy of the surroundings
Second Law and Temperature
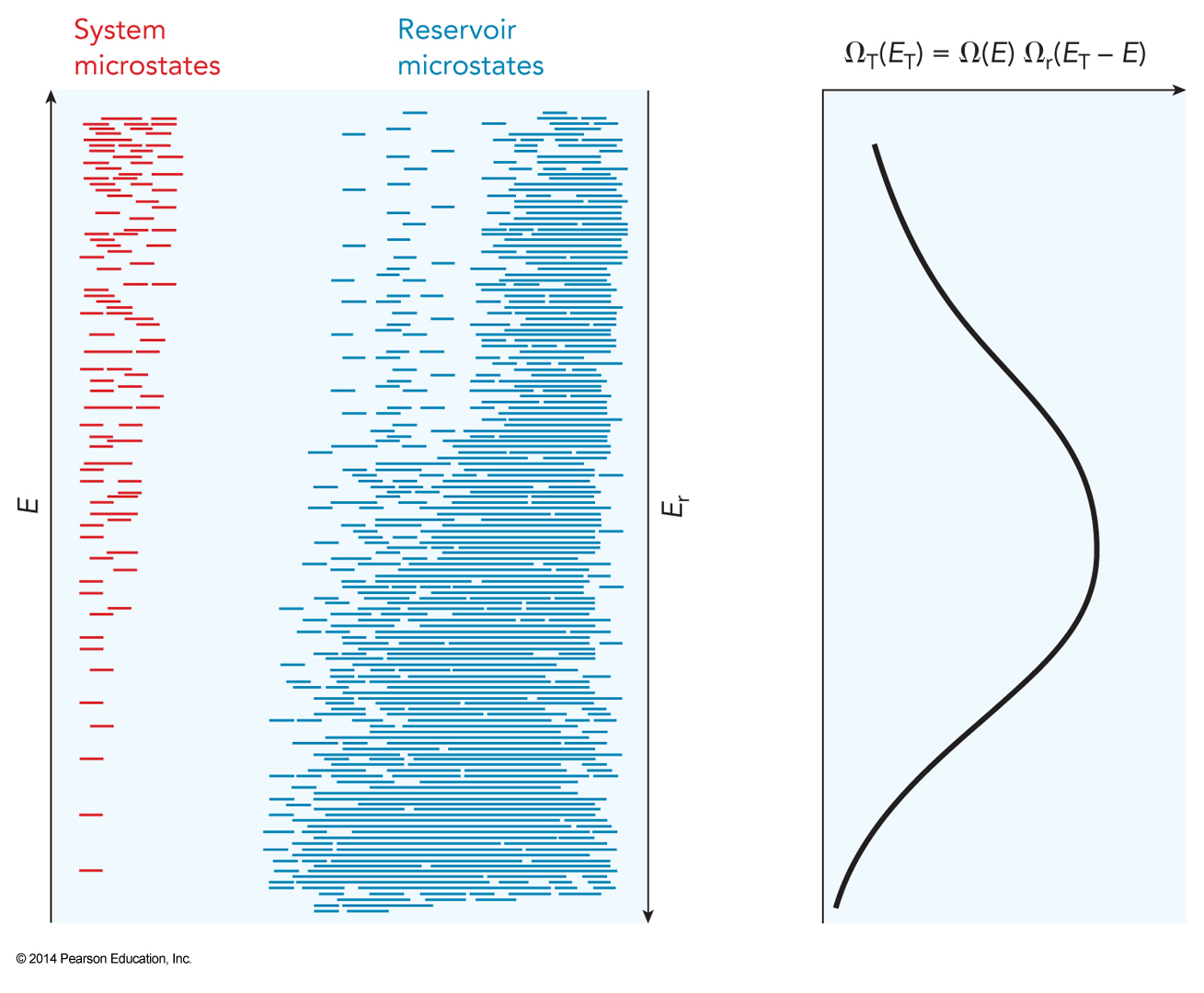
- Let’s look at the system in thermal contact with a reservoir (from chapter 2)
- System had fixed volume and number of particles
- It could exchange energy with the surrounding reservoir as long and \(E_T\) was conserved.
- Let’s look at the effects of the second law on this system.
- As energy is transferred into the system from the reservoir
- Energy of the system rises
- \(\Omega(E)\) rises (this is the system)
- Energy of the reservoir falls
- \(\Omega_r(E_r)\) falls (this is the reservoir)
- As long as there are no additional interactions then \(\Omega_T(E_T)=\Omega(E)\Omega_r(E_r)\)
The Take-Away
- Based on that equation we know that if either ensemble size gets too small then the total ensemble size will decrease
- This means that the configuration with the most available microstates is somewhere in the middle
System and Reservoir Microstates
Finding the Largest Ensemble State
- We can find this maximum total by first keeping V and n constant for both the reservoir and the system and setting derivative equal to zero $$ \begin{align} \left. \left(\frac{\partial \ln \Omega_T}{\partial E}\right)_{V,n}\right|_\chem{max} &= 0 = \left. \left(\frac{\partial \ln \left(\Omega \Omega_r\right)}{\partial E}\right)_{V,n} \right|_\chem{max} \\ &= \left. \left(\frac{\partial \left(\ln \Omega+\ln \Omega_r\right)}{\partial E}\right)_{V,n} \right|_\chem{max} \\ &= \left. \left(\frac{\partial \ln \Omega}{\partial E}\right)_{V,n} \right|_\chem{max} + \left. \left(\frac{\partial \ln \Omega_r}{\partial E}\right)_{V,n} \right|_\chem{max} \\ \end{align} $$
- Because \(E+E_r=E_T\) is constant then \(dE=-dE_r\) $$ 0 = \left. \left(\frac{\partial \ln \Omega}{\partial E}\right)_{V,n} \right|_\chem{max} - \left. \left(\frac{\partial \ln \Omega_r}{\partial E_r}\right)_{V,n} \right|_\chem{max} $$
Finding the Largest Ensemble State Continued
$$ 0 = \left. \left(\frac{\partial \ln \Omega}{\partial E}\right)_{V,n} \right|_\chem{max} - \left. \left(\frac{\partial \ln \Omega_r}{\partial E_r}\right)_{V,n} \right|_\chem{max} $$ $$ \begin{align} \left. \left(\frac{\partial \ln \Omega}{\partial E}\right)_{V,n} \right|_\chem{max} &= \left. \left(\frac{\partial \ln \Omega_r}{\partial E_r}\right)_{V,n} \right|_\chem{max} \\ \left. \left(\frac{\partial S}{\partial E}\right)_{V,n}\right|_\chem{max} &= \left. \left(\frac{\partial S_r}{\partial E_r}\right)_{V,n}\right|_\chem{max} \\ \frac{1}{T} &= \frac{1}{T_r} \Rightarrow T=T_r \end{align} $$
What Does this Mean?
$$ T=T_r $$
- The condition that leads to the maximum total entropy is when the sample and the reservoir have the same temperature
- For an ideal gas, this saying that the sample and reservoir have come to the same temperature
- So, when they contact, the hot one will lose energy (\(T\)) and the cold will gain energy (\(T\))
- So...
- Heat flows from a hot body to a cold body
- Because the maximum entropy is found when the two arrive at the same temperature
- Heat flows from a hot body to a cold body
Clausius Principle
- The Clausius principle is another way of phrasing the second law of thermodynamics $$ \left(\Delta S_T\right)_{E,V,n} \ge 0 $$
- The equality only hold for a reversible process
- For any irreversible process, the total entropy will increase
- Note: a process in which the total entropy increases is called spontaneous
Reversible and Adiabatic
- A reversible process is one in which to total entropy remains constant $$ \text{reversible: }\Delta S_T = 0 $$
- An adiabatic process is one in which \(q=0\)
- So for a reversible and adiabatic process we have $$ \text{reversible and adiabatic: }\Delta S=0 $$
- In the world we also have non-adiabatic reversible and irreversible adiabatic processes
Change in Entropy
- We want to determine the change in entropy of an ideal gas undergoing isothermal expansion from \(V_i\) to \(V_f\)
- During isothermal expansion the energy of the gas does not change
- Ideal gas energy only depends on temperature
- For an expansion \(V_f \gt V_i\) therefore \(\Delta S\) is positive
- \(\Delta S\) is negative for compression
Notes
- It is important to remember that energy, entropy, temperature, volume, pressure, and number of moles are all state function
- This means is does not matter how we go between initial and final states
- It also means that \(\Delta E\), \(\Delta S\), \(\Delta T\), \(\Delta V\), \(\Delta P\), and \(\Delta n\) also do not depend on the path taken
- \(\Delta S_T\) does depend on path
Why Does \(\Delta S_T\) Depend on Path?
- Consider \(\Delta E_\chem{rev}\) for a reversible process and \(\Delta E_\chem{irr}\) for an irreversible process $$ q_\chem{rev} + w_\chem{rev} = \Delta E_\chem{rev} = \Delta E_\chem{irr} = q_\chem{irr}+w_\chem{irr} $$
- As we have shown previously for the isothermal expansion, the reversible process is the one that did the most work, so for any process $$ 0 \gt w_\chem{irr} \gt w_\chem{rev},\,q_\chem{irr}\lt q_\chem{irr} $$
- For the reversible process \(\dbar q_\chem{rev} = T\, dS\)
- This gives the Clausius inequality
$$ \dbar q \le T\,dS $$
- The equality only holds for the reversible process
Thermodynamic Potentials
- The thermodynamic potentials can also give the direction of spontaneous process on certain conditions
- We rarely measure entropy directly
- We don’t often want to hold \(E\) and \(V\) constant
- If we keep \(T\) and \(P\) constant, the Gibbs energy is useful
Gibbs Energy
- From our Gibbs energy definition in chapter 7 $$ \begin{align} G &= E-TS+PV \\ dE &= \dbar q + \dbar w \\ \left(dG\right)_{T,P} &= \left( dE-T\,dS-S\,dT+P\,dV + V\,dP \right)_{T,P} \\ &= \dbar q+\dbar w - T\,dS + P\,dV \end{align} $$
So what?
- From the Clausius inequality we know \(\dbar q \le T\,dS\)
- We know the maximum work is done in a reversible process so \(\dbar w = \dbar w_\chem{rev} \ge -P\,dV\)
- So, if we only consider \(PV\) work then \(\left(dG\right)_{T,P} \le 0\)
- Again, the equality hold only for reversible processes
- \(A\) process is spontaneous under constant \(T\) and \(P\) that will minimize \(G\)
- \(G\) is at its minimum value at equilibrium
In Benchtop Chemistry
- The direction in which the reaction will move spontaneously is the one that leads to a negative \((\Delta G)_T\), where $$ \begin{align} (\Delta G)_T &= \Delta (H-TS)_T \\ &= (\Delta H)_T - (T\Delta S + S\Delta T)_T \\ &= (\Delta H)_T - T(\Delta S)_T \end{align} $$
- If temperature is understood to be fixed then $$ \Delta G = \Delta H - T\Delta S $$
- The change in enthalpy is equal to the heat flowing into the surrounding bath which can be related to \(\Delta S_r\) $$ \Delta H = q = -q_r = -T\Delta S_r $$
- So using this in our equations we have $$ (\Delta G)_{T,P} = -T\Delta S_r -T\Delta S=-T(\Delta S_r+\Delta S) $$
Ideal Mixing
The Setup
- We have two containers each holding an ideal gas at the same temperature and pressure
- Container \(\chem{A}\) holds \(n_\chem{A}\) moles of gas
- Container \(\chem{B}\) holds \(n_\chem{B}\) moles of gas
- The containers are connected through a tube with a valve
- What happens to the entropy and other parameters when the value is opened?
Intuition
- Intuitively we know that this mixing will be spontaneous
- This means that the entropy must increase
- How can this be true when the density of gas throughout the containers is never changing.
- Volume evolution: $$ \begin{align} \text{gas A: } V_\chem{A} &\rightarrow V_\chem{A}+V_\chem{B} \\ \text{gas B: } V_\chem{B} &\rightarrow V_\chem{A}+V_\chem{B} \end{align} $$
Each Gas
- We know that expanding each gas individually increases its entropy $$ \begin{align} dS &= \frac{P}{T}dV=\frac{nR}{V}dV \\ \Delta S &= nR\ln \left(\frac{V_f}{V_i}\right) \\ \Delta S_\chem{A} &= n_\chem{A}R\ln \left(\frac{V_\chem{A}+V_\chem{B}}{V_\chem{A}}\right) \\ \Delta S_\chem{B} &= n_\chem{B}R\ln \left(\frac{V_\chem{A}+V_\chem{B}}{V_\chem{B}}\right) \end{align} $$
Volume to Moles
- Because we are at constant temperature and pressure, we can rewrite our equation in terms of mole fractions $$ \begin{align} \frac{V_\chem{A}}{V_\chem{A}+V_\chem{B}} &= \frac{n_\chem{A}}{n_\chem{A}+n_\chem{B}} = X_\chem{A} \\ \frac{V_\chem{B}}{V_\chem{A}+V_\chem{B}} &= \frac{n_\chem{B}}{n_\chem{A}+n_\chem{B}} = X_\chem{B} \end{align} $$
- Therefore $$ \Delta_\chem{mix}S=n_\chem{A}R\ln \frac{1}{X_\chem{A}} + n_\chem{B}R\ln\frac{1}{X_\chem{B}}=-R\left( n_\chem{A}\ln X_\chem{A}+n_\chem{B}\ln X_\chem{B} \right) $$
What Does this Equation Tell Us?
$$ \Delta_\chem{mix}S=n_\chem{A}R\ln \frac{1}{X_\chem{A}} + n_\chem{B}R\ln\frac{1}{X_\chem{B}}=-R\left( n_\chem{A}\ln X_\chem{A}+n_\chem{B}\ln X_\chem{B} \right) $$
- By definition, mole fractions are less than one.
- This means that \(\ln X\) must be negative
- This means that the entropy of mixing must be positive
- This means that the ideal mixing must be spontaneous
- What is driving this process?
Rewriting Our Ensemble Size Enough Again
- It is convenient to rewrite out ensemble size equation again $$ \begin{align} \Omega_k^\chem{trans} &= V_k^{N_k} f(E_k,N_k) \\ f(E_k,N_k) &= \left\{ \begin{split} & \frac{1}{N_K!\left[ \left(\frac{3N_k}{2}\right)-1 \right]!} \left(\frac{\pi}{4}\right) \left(\frac{2\pi m_kE_k}{h^2}\right)^{\frac{3N_k}{2}} \\ & \left(\frac{h^2}{2\pi m_kE_kV_k^\bfrac{2}{3}}\right) \end{split} \right\} \\ k &= \text{A or B} \end{align} $$
- We label is trans because the translation term is what allows the particles to mix
Allowing for More Stuff
- We may need to factor in degeneracies for the intermolecular vibrational states, rotations, and other internal degrees of freedom
- Including those contributions increases the number of available microstates by \(\Omega^\chem{int}\) $$ \begin{align} S_i &= S_\chem{A}+S_\chem{B} = k_\mathrm{B}\left(\ln \Omega_\chem{A}+\ln \Omega_\chem{B}\right) \\ &= k_\mathrm{B}\left[ \ln \left( \Omega_\chem{A}^\chem{int}\Omega_\chem{A}^\chem{trans} \right) + \ln \left( \Omega_\chem{B}^\chem{int}\Omega_\chem{B}^\chem{trans} \right) \right] \\ &= k_\mathrm{B} \left\{ \begin{split} & \ln \left[ \Omega_\chem{A}^\chem{int} f(E_\chem{A},N_\chem{A})V_\chem{A}^{N_\chem{A}} \right] \\ & + \ln \left[ \Omega_\chem{B}^\chem{int} f(E_\chem{B},N_\chem{B})V_\chem{B}^{N_\chem{B}} \right] \end{split} \right\} \\ &= \left[ \begin{split} & k_\mathrm{B} \left\{ \ln \left[ \Omega_\chem{A}^\chem{int} f(E_\chem{A},N_\chem{A}) \right] + \ln \left[ \Omega_\chem{B}^\chem{int} f(E_\chem{B},N_\chem{B}) \right] \right\} \\ & +N_\chem{A}k_\mathrm{B}\ln V_\chem{A} + N_\chem{B} k_\mathrm{B} \ln V_\chem{B} \end{split} \right] \end{align} $$
- Doing the same thing for the final entropy $$ S_f = \left[ \begin{split} & k_\mathrm{B} \left\{ \ln \left[ \Omega_\chem{A}^\chem{int} f(E_\chem{A},N_\chem{A}) \right] + \ln \left[ \Omega_\chem{B}^\chem{int} f(E_\chem{B},N_\chem{B}) \right] \right\} \\ & + (N_\chem{A}+N_\chem{B})k_\mathrm{B} \ln (V_\chem{A}+V_\chem{B}) \end{split} \right] $$
If That Wasn't Enough Fun, Now We Take the Difference
$$ \left[ \begin{split} & k_\mathrm{B} \left\{ \ln \left[ \Omega_\chem{A}^\chem{int} f(E_\chem{A},N_\chem{A}) \right] + \ln \left[ \Omega_\chem{B}^\chem{int} f(E_\chem{B},N_\chem{B}) \right] \right\} \\ & +N_\chem{A}k_\mathrm{B}\ln V_\chem{A} + N_\chem{B} k_\mathrm{B} \ln V_\chem{B} \end{split} \right] $$ $$ S_f = \left[ \begin{split} & k_\mathrm{B} \left\{ \ln \left[ \Omega_\chem{A}^\chem{int} f(E_\chem{A},N_\chem{A}) \right] + \ln \left[ \Omega_\chem{B}^\chem{int} f(E_\chem{B},N_\chem{B}) \right] \right\} \\ & + (N_\chem{A}+N_\chem{B})k_\mathrm{B} \ln (V_\chem{A}+V_\chem{B}) \end{split} \right] $$
- Note that the first term in each are identical so they will cancel out when we take the difference $$ \begin{align} \Delta S_\chem{mix} =& S_f - S_i \\ =& (N_\chem{A}+N_\chem{B})k_\mathrm{B} \ln (V_\chem{A}+V_\chem{B}) - \left[ (N_\chem{A}+N_\chem{B})k_\mathrm{B} \ln (V_\chem{A}+V_\chem{B}) \right] \\ & \vdots \\ =& -R\left(n_\chem{A}\ln X_\chem{A}+n_\chem{B}\ln X_\chem{B}\right) \end{align} $$
Result
- So we got the same result that we get classically.
- Now we have shown that as long as the A-B interaction is essentially the same as the A-A and B-B interactions it doesn’t matter if we are dealing with gases or liquids, monatomics or polyatomics.
- The number of distinct translational states increases by a factor of \( \frac{\left(V_\chem{A}+V_\chem{B}\right)^{N_\chem{A}+N_\chem{B}}}{V_\chem{A}^{N_\chem{A}}V_\chem{B}^{N_\chem{B}}} \)
Ultimate Results
- Even with no work done and no net heat flow, system will evolve so as to find more microstates of the ensemble
- The driving force behind mixing has nothing to do with the mixing itself
- Each substance is taking advantage of the opportunity to distribute its particles over a greater volume thereby increasing its own entropy.
Free Energy of Mixing
- We can calculate the Gibbs free energy of mixing the same way $$ \begin{align} \Delta_\chem{mix} G &= \Delta G_\chem{A} + \Delta G_\chem{B} = \int_i^f dG_\chem{A} + \int_i^f dG_\chem{B} \\ &= \int_i^f \left( \begin{split} & -S_\chem{A}\,dT_\chem{A} \\ & + V_\chem{A}\,dP_\chem{A} \end{split} \right)_T + \int_i^f \left( \begin{split} & -S_\chem{B}\,dT_\chem{B} \\ & + V_\chem{B}\,dP_\chem{B} \end{split} \right)_T \\ &= \int_i^f \left( V_\chem{A}\,dP_\chem{A} \right)_T + \int_i^f \left( V_\chem{B}\,dP_\chem{B} \right)_T \\ &= n_\chem{A}RT \int_i^f \frac{dP_\chem{A}}{P_\chem{A}} + n_\chem{B}RT \int_i^f \frac{dP_\chem{B}}{P_\chem{B}} \\ &= RT \left( n_\chem{A} \ln \frac{P_\chem{A}}{P} + n_\chem{B} \ln \frac{P_\chem{B}}{P} \right) \\ &= RT \left( n_\chem{A}\ln X_\chem{A}+n_\chem{B}\ln X_\chem{B} \right) \end{align} $$
Enthalpy of Mixing
- We can calculate the enthalpy change of mixing the same way (remember that \(T\) is constant) $$ \begin{align} \Delta G &= \Delta H - T\Delta S\\ \Delta H_\chem{mix} &= \Delta_\chem{mix}G + T\Delta_\chem{mix}S \\ &= \left\{ \begin{split} & RT\left(n_\chem{A}\ln X_\chem{A}+n_\chem{B}\ln X_\chem{B}\right) \\ & + T\left[-R\left(n_\chem{A}\ln X_\chem{A}+n_\chem{B}\ln X_\chem{B}\right)\right] \end{split} \right\} \\ &= 0 \end{align} $$
- So, because the process takes place at constant pressure, \(\Delta H=q\), and no heat is flowing, so $$ \Delta H =0 $$
The Third Law of Thermodynamics
The Third Law of Thermodynamics
- Up to this point we have basically limited ourselves to calculating changes in entropy
- We need a reference value for entropy
- This reference is given in the third law of thermodynamics
- The entropy of a substance approaches a minimum as \(T\) approaches zero
- We also \(S=0\) at \(T=0\)
Problem
- There is an experimental problem with this law
- At absolute zero, the most stable form of a substance is a crystal that puts each particle in the most stable, reproducible place.
- At very cold temps, however, the atoms don’t have enough energy to cross the energy barrier separating crystalline phases
- Crystal domains form - local ordered regions
Meaning
- Cooling the substance traps it in any of several low-energy state
- Not necessarily the lowest energy state
- This means there is residual entropy that cannot be removed from the system
- This means there are still several ensemble states possible
- Thus \(S=k_\mathrm{B} \ln \Omega \ne 0\), but it is close to zero
Getting to Absolute Zero
- It is thermodynamically impossible to reach absolute zero
- Near absolute zero it also because quantum mechanically impossible to reach absolute zero
- Getting there would involve remove all molecular motion
- We can get to less that \(1\,\mathrm{K}\) using boiling liquid helium as a coolant
The Curie Temperature
- Magnetic material have a temperature at with the thermal motion of the atom (called phonons) exceed the force keeping the spins aligned (magetism).
- The temperature this occurs at is called the Curie temperature
- Iron has a Curie temperature of \(1043\,\mathrm{K}\)
- Many substances become magnetic at some low temperature
Adiabatic Demagnetization; Step 1
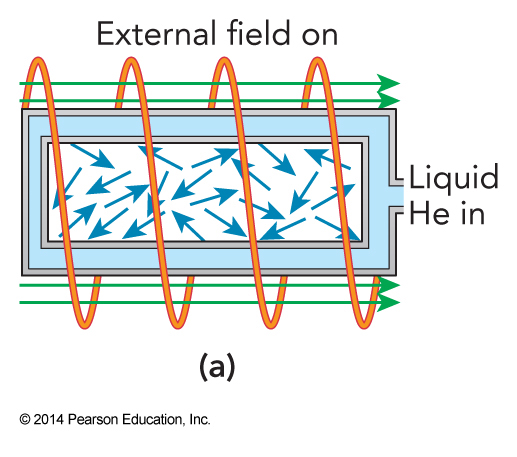
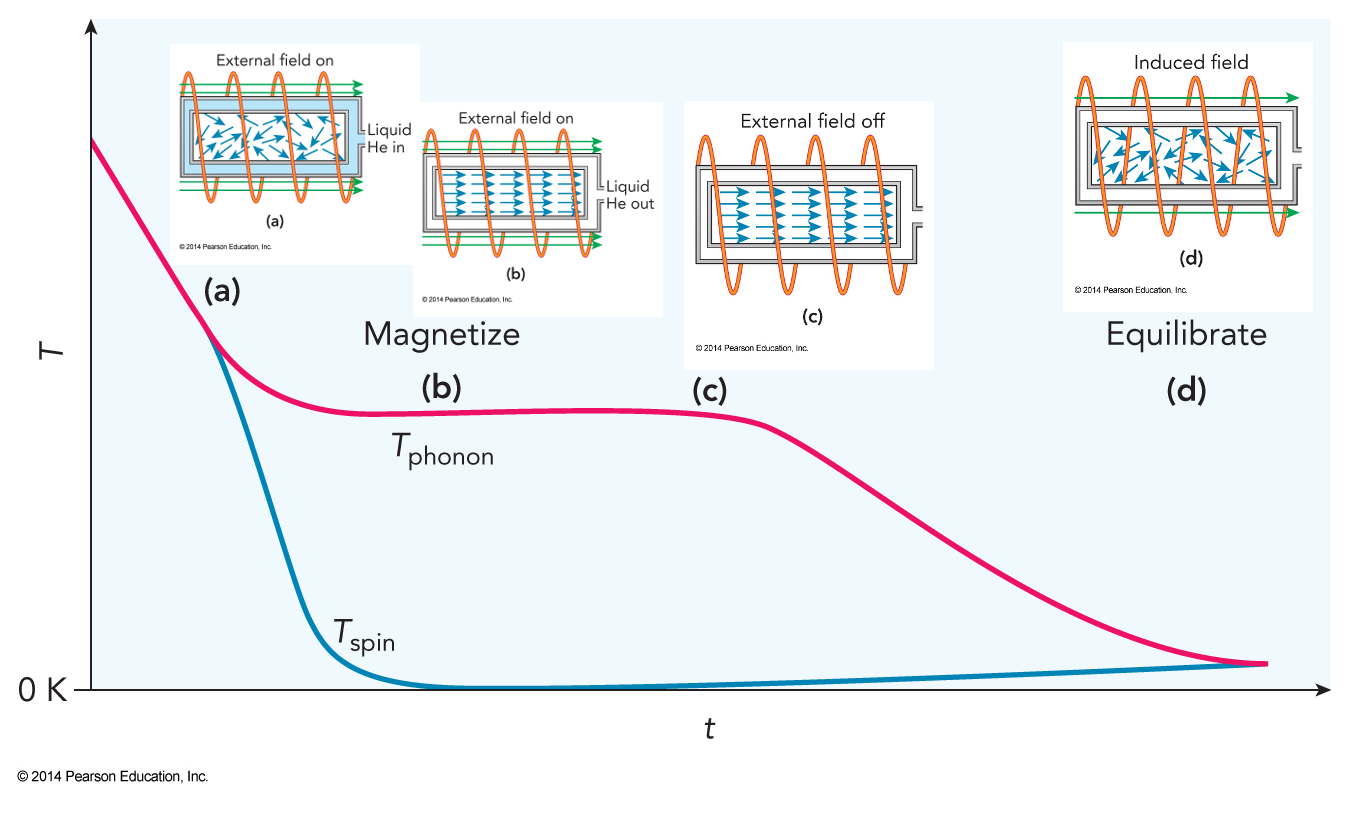
Liquid helium is used to cool a crystal to near \(1\,\mathrm{K}\) as it is magnetized by a high-field external solenoid magnet.
Adiabatic Demagnetization; Step 2
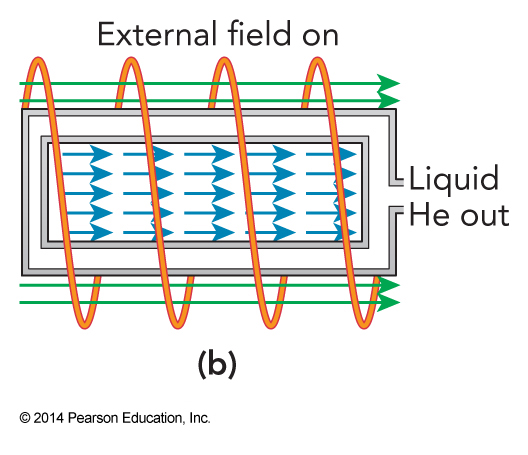
The helium is replaced by vacuum once the crystal is fully magnetized.
Adiabatic Demagnetization; Step 3
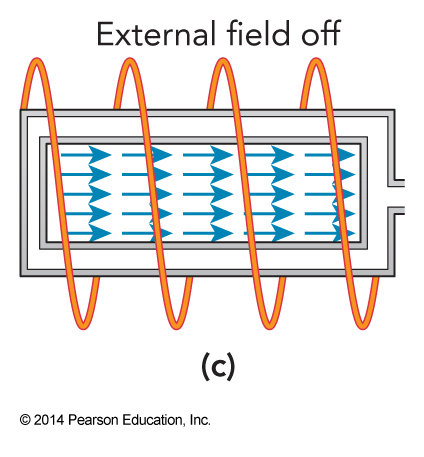
The external field is turned off.
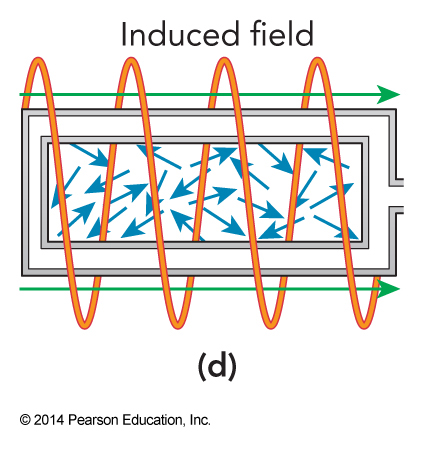
Adiabatic Demagnetization; Step 4
- The spins in the crystal equilibrate with the phonons.
- The net angular momentum of the spins is conserved by a current induced in the solenoid, which does work and further lowers the temperature of the crystal.
- Final temperatures below \(10^{-6}\,\mathrm{K}\) can be achieved using this technique.
Adiabatic Demagnetization: Effect on Temperature
The Debye Theory
- At constant pressure $$ S=\int_0^T \frac{C_P(T')}{T'}dT' $$
- The Debye theory for heat capacities predicts a low temperature heat capacity $$ C_V \approx \frac{12\pi^4 Nk_\mathrm{B}^4 T^3}{5\omega_\mathrm{D}^3} $$
The Debye Theory Continued
- For crystals, the heat capacity at constant pressure is nearly equal to \(C_V\)
- Thermal expansion is very small
Standard Molar Entropies
- Most thermodynamic quantities (e.g. \(\Delta G\), \(\Delta H\), etc.) are tabulated relative to some reference
- Entropy of a compound is tabulated as the absolute, standard molar entropy, \(S_\chem{m}^\ominus\)
- Pure substance
- Pressure of exactly \(1\,\mathrm{bar}\)
Selected Standard Molar Entropies
| Substances | \(S_\chem{m}^\ominus\; (\mathrm{J\,K^{-1}\,mol^{-1}})\) | Substances | \(S_\chem{m}^\ominus\; (\mathrm{J\,K^{-1}\,mol^{-1}})\) |
|---|---|---|---|
| Diatomic gases | Tetratomic gases | ||
| \(\chem{Br_2(g)}\) | 245.463 | \(\chem{ClF_3(g)}\) | 281.61 |
| \(\chem{CO(g)}\) | 197.674 | \(\chem{SO_3(g)}\) | 256.76 |
| \(\chem{F_2(g)}\) | 202.78 | \(\chem{SO_2Cl_2(g)}\) | 311.94 |
| \(\chem{HF(g)}\) | 173.779 | Liquids | |
| \(\chem{HI(g)}\) | 206.594 | \(\chem{H_2O(l)}\) | 69.91 |
| \(\chem{KCl(g)}\) | 239.10 | \(\chem{Br_2(l)}\) | 152.231 |
| \(\chem{O_2(g)}\) | 205.138 | \(\chem{CS_2(l)}\) | 151.34 |
| \(\chem{SiN(g)}\) | 216.76 | Solids | |
| Tetratomic gases | \(\chem{C(diamond)}\) | 2.377 | |
| \(\chem{C_2H_2(g)}\) | 200.94 | \(\chem{C(graphite)}\) | 5.740 |
| \(\chem{COCl_2(g)}\) | 283.53 | \(\chem{SiO_2(quartz)}\) | 41.84 |
Computer Simulations
Due to limited time, we are going to skip the final section of this chapter.
/