The First Law: Expansion and Engines
Shaun Williams, PhD
Expansion of Gases
Isothermal Expansion
- Consider the work done in the reversible expansion between two thermodynamic states
- \(V_2 \gt V_1\)
- The first law states $$ dE = \dbar q + \dbar w =T\,dS - P\,dV+\mu\,dn $$
- If we restrict ourselves to a closed system then \(dn = 0\) so $$ dE=\dbar q+\dbar w = T\,dS-P\,dV $$
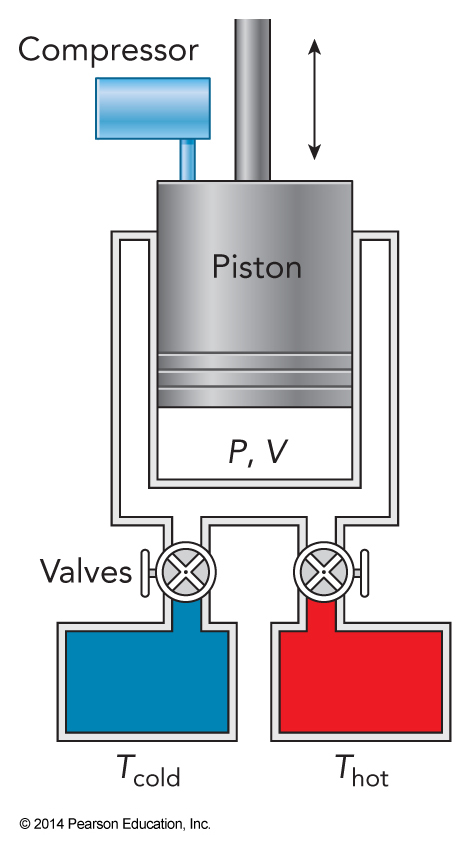
Our Expansion Setup
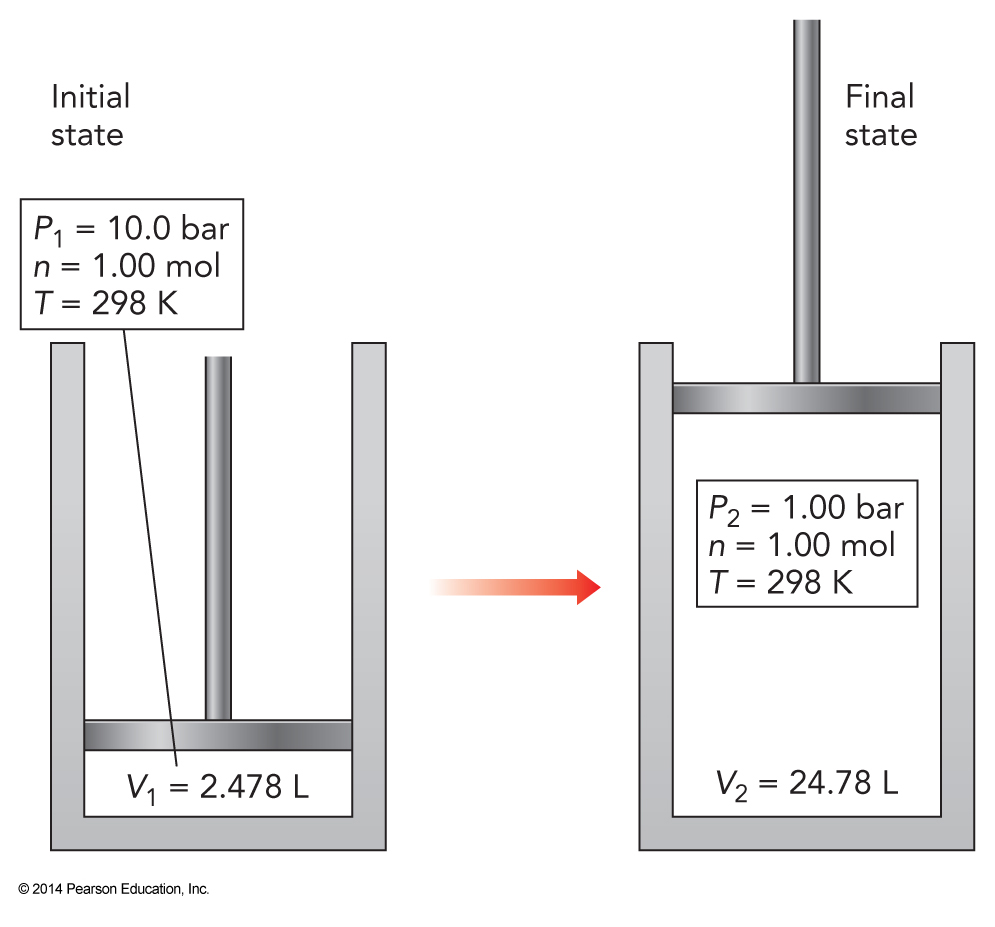
More Simplifications
- If our process is reversible then from the last chapter \(\dbar q_{rev} = T\,dS\)
- This means that \(\dbar w_{rev}=-P\,dV\)
- Let’s say this is an isothermal expansion
- Using a heat reservoir and diathermal walls $$ w_{T,rev} = \int_{V_1}^{V_2} \dbar w_{T,rev} = -\int_{V_1}^{V_2} P\,dV $$
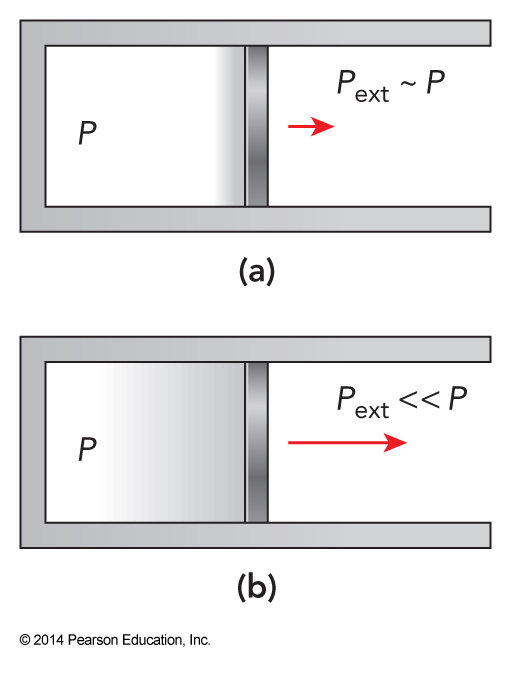
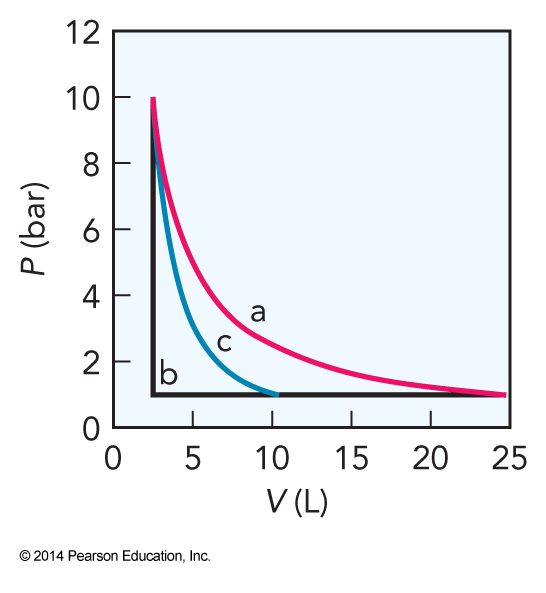
Reversible vs Irreversible Expansions
Applying the Ideal Gas Law
- From the ideal gas law we know that \(P=\frac{nRT}{V}\)
- Using this we find that $$ \begin{align} w_{T,rev} &= -\int_{V_1}^{V_2} P\,dV = -nRT \int_{V_1}^{V_2}\frac{dV}{V} \\ &= -nRT \ln \left(\frac{V_2}{V_1}\right) \end{align} $$
Example 8.1
A vacuum chamber in a spectrometer is maintained at an operating pressure of \(10.0\,\mathrm{mtorr}\) by a two-stage rotary vane pump with an exhaust pressure at the pump outlet of \(800.\,\mathrm{torr}\). What is the minimum power in watts (\(\mathrm{\bfrac{J}{s}}\)) consumed by the pump to keep the chamber at this pressure when there is a flow of \(0.22\,\mathrm{\bfrac{mmol}{s}}\) and \(T=300\,\mathrm{K}\)?
For an Irreversible Case
- If we have an irreversible expansion with a constant external pressure of \(P_{min}\) $$ \begin{align} w_{T,irr} &= \int_{V_1}^{V_2}\dbar w_{irr} \\ &= -\int_{V_1}^{V_2} P_{min}\,dV \\ &= -P_{min} \left(V_2-V_1\right) \end{align} $$
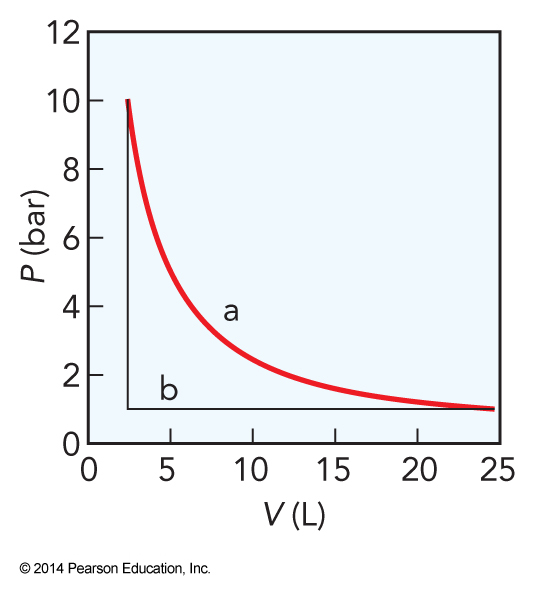
Plots of Pressure vs Volume for Reversible vs Irreversible Expansions
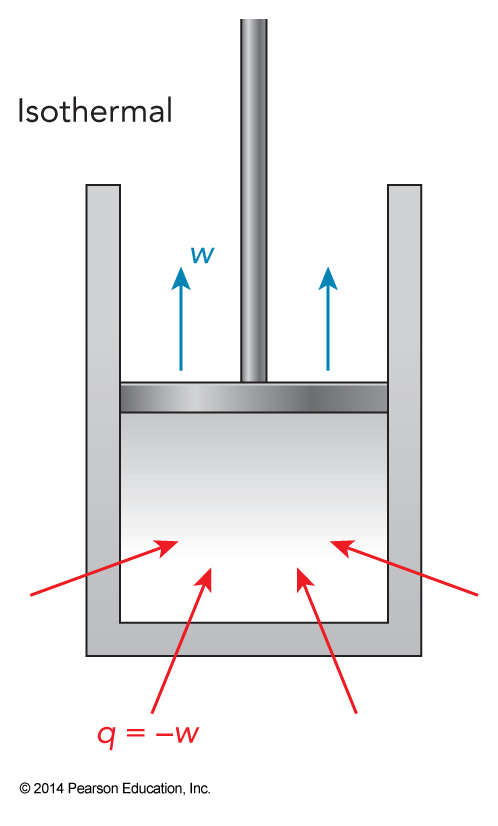
The Balance of Energy Flow in Isothermal Expansion
More Ideal Gas Approximations
- For an ideal gas we know that \(E=\frac{3}{2}nRT\)
- This means that for a closed, isothermal expansion, \(\Delta E=0\)
- Therefore $$ \begin{align} \Delta E = q+w &=0 \\ q_{T,rev} - nRT\ln \left(\frac{V_2}{v_1}\right) &= 0 \\ q_{T,rev} &= nRT \ln \left( \frac{V_2}{V_1}\right) \\ q_{T,irr} &= P_{min} \left(V_2-V_1\right) \end{align} $$
Something to Notice
- Even though this is a reversible process and \(dS_T=0\) $$ \dbar q_{rev} \ne 0 $$
- This means that for the system $$ dS = \frac{\dbar q}{T} \ne q $$
- This means that the reservoir must respond with its own entropy change that exactly cancels the sample’s entropy change
Reversible Adiabatic Expansion
- In an adiabatic expansion, no heat can flow through the boundary walls, thus $$ \dbar q_{rev} = T\,dS =0 $$
- This means that \(dE=\dbar w_{S,rev} = -P\,dV\)
- Continuing to assume only \(PV\) work and that we have a closed system $$ dE = -P\,dV = -\frac{nRT\,dV}{V} $$
Problems!
$$ dE=-P\,dV = -\frac{nRT\,dV}{V} $$
- Because the sample container is adiabatic, the sample temperature can change during the expansion
- If the temperature changes, which it will, the final volume will also change
- We need another equation so we can tell how the temperature and volume change
Welcome Back Heat Capacity!
- The heat capacity relates \(\Delta E\) and \(\Delta T\)
- For an ideal gas \(E=\frac{1}{2}N_{ep}nRT\)
- Now let’s do some math $$ \begin{align} dE &= \left(\frac{\partial E}{\partial T}\right)_VdT=C_V\,dT \\ C_V\,dT &= -\frac{nRT\,dV}{V} \\ \int_{T_1}^{T_2} \frac{C_V\,dT}{T} &= -\int_{V_1}^{V_2} \frac{nR\,dV}{V} \\ C_V\ln\frac{T_2}{T_1} &= -nR\ln \frac{V_2}{V_1} \\ V_2 &= V_1 \left(\frac{P_2}{P_1}\right)^{-\frac{C_V}{C_P}} \end{align} $$
More Expansion Stuff
- The work done during the expansion is equal to $$ \Delta E = C_V \Delta T $$
- Thus $$ \begin{align} w_{S,rev} &= C_V (T_2 - T_1) \\ &= C_V \left[ \frac{P_2V_2}{nR}-\frac{P_1V_1}{nR}\right] \\ &= \frac{C_V}{nR}\left[P_2V_1\left(\frac{P_2}{P_1}\right)^{-\bfrac{C_V}{C_P}}-P_1V_1\right] \\ &= \frac{C_V}{nR}(P_1V_1)\left[\frac{P_2}{P_1}\left(\frac{P_2}{P_1}\right)^{-\bfrac{C_V}{C_P}}-1\right] \end{align} $$
More Derivation
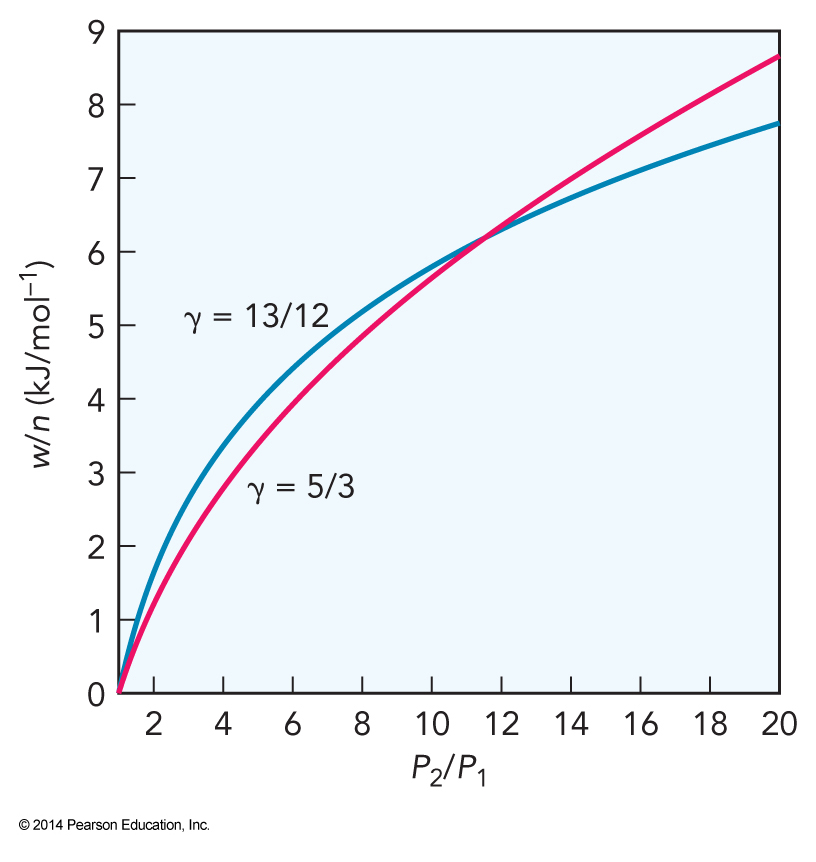
- Continuing on $$ \begin{align} w_{S,rev} &= \frac{C_V}{C_P-C_V}(P_1V_1)\left[\left(\frac{P_2}{P_1}\right)^{1-\bfrac{C_V}{C_P}}-1\right] \\ &= \frac{1}{\bfrac{C_P}{C_V}-1} (P_1V_1)\left[\left(\frac{P_2}{P_1}\right)^{1-\bfrac{C_V}{C_P}}-1\right] \\ &= \frac{P_1V_1}{\gamma-1}\left[\left(\frac{P_2}{P_1}\right)^{1-\bfrac{1}{\gamma}}-1\right] \end{align} $$
- Note the heat capacity ratio \(\gamma = \bfrac{C_P}{C_V}\)
Three Plots
Compression Ratios and Work
Example 8.2
If \(1.0\,\mathrm{L}\) of hexamethylene triperoxide diamine (HMTD) explodes by suddenly decomposing to gases at a pressure of \(1.0\,\mathrm{kbar}\) at the ambient temperature, calculate the grams of TNT that would release a pressure wave of equal energy, assuming \(4680\,\mathrm{\bfrac{J}{g\,TNT}}\), and assuming the explosion is reversible. Assume an average value of \(\gamma\) of \(1.4\), an ambient pressure of \(1.0\,\mathrm{bar}\), and that 70% of the energy is in the pressure wave.
Special Case
- Let’s look at an adiabatic expansion in which the enthalpy is held constant while \(P\), \(V\), and \(T\) can change
- A gas is in one chamber separated by a permeable plug
- A piston compresses the gas in the chamber forcing it through the plug
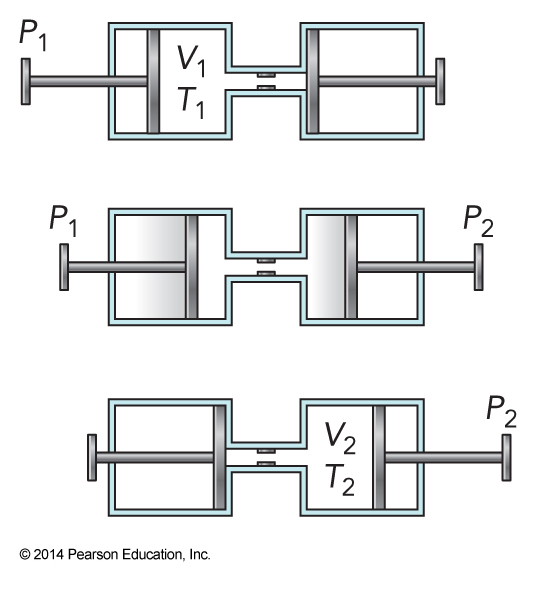
The Math
- No heat can flow so \(\Delta E=w_2+w_1\)
- Because we kept the pressure in each container constant the work in each container is just \(–P\Delta V\) $$ \Delta E = -P_2V_2 - P_1(-V_1) = P_1V_1-P_2V_2 $$
- Look at the enthalpy $$ \begin{align} \Delta H &= \Delta (E+PV) \\ &= \Delta E + \Delta (PV) \\ &= (P_1V_1-P_2V_2) + (P_2V_2-P_1V_1) \\ &= 0 \end{align} $$
The Special Expansion
- This special type of adiabatic expansion is called the Joule-Thomson expansion
- Named for James Joule and William Thomson
- Both of whom have very common units named after them
Temperature Change?
- What happens to the temperature of the gas as it passes through the plug between pressures
- We are looking for the Joule-Thomson coefficient \(\left(\frac{\partial T}{\partial P}\right)_H\) $$ \left(\frac{\partial T}{\partial P}\right)_H=-\left(\frac{\partial T}{\partial H}\right)_P\left(\frac{\partial H}{\partial P}\right)_T = -\frac{1}{C_P}\left(\frac{\partial H}{\partial P}\right)_T $$
- Simplifying $$ \begin{align} \left(\frac{\partial H}{\partial P}\right)_T &= \left( \frac{T\partial S+V\partial P}{dP}\right)_T = \left( \frac{T\partial S}{dP}\right)_T+\left(\frac{V\partial P}{dP}\right)_T \\ &= T\left(\frac{\partial S}{\partial P}\right)_T+V \\ &= -T\left(\frac{\partial V}{\partial T}\right)_P+V=-TV\alpha +V \\ \left(\frac{\partial T}{\partial P}\right)_H &= \frac{TV\alpha -V}{C_P} \end{align} $$
Joule-Thomson Coefficient for a Real Gas
- Consider a gas governed by the second virial expansion \(P=RT\left[V_m^{-1}+B_2(T)V_m^{-2}\right]\) $$ V=\frac{nRT}{P}\left(1+\frac{n}{V}B_2(T)\right) $$
- thus $$ \begin{align} V\alpha &= \left(\frac{\partial V}{\partial T}\right)_P \\ &= \frac{nR}{P}\left(1+\frac{n}{V}B_2(T)\right) +\frac{nRT}{P}\left[\begin{split} & -\frac{n}{V^2}B_2(T)\left(\frac{\partial V}{\partial T}\right)_P \\ &+\frac{n}{V}\left(\frac{\partial B_2}{\partial T}\right)_P\end{split}\right] \\ &= \frac{V}{T}+\frac{nRT}{P}\left[-\frac{n}{V^2}B_2(T)\left(\frac{\partial V}{\partial T}\right)_P+\frac{n}{V}\left(\frac{\partial B_2}{\partial T}\right)_P\right] \end{align} $$
Imagine A LOT of Math
- After a lot more algebra, calculus, etc we arrive at $$ \left(\frac{\partial T}{\partial P}\right)_H = \frac{T\left(\frac{\partial B_2}{\partial T}\right)_P-B_2(T)}{C_{Pm}} $$
- In terms of the van der Waals coefficients $$ \left(\frac{\partial T}{\partial P}\right)_H = \frac{\frac{2a}{RT}-b}{C_{Pm}} $$
Limits of the Equation
- At high temperatures $$ \left(\frac{\partial T}{\partial P}\right)_H \approx -\frac{b}{C_{Pm}} $$
- At low temperatures $$ \left(\frac{\partial T}{\partial P}\right)_H \approx \frac{2a}{RTC_{Pm}} $$
Joule-Thomson Experiment Different Limits
- Attractive forces dominate
- Attractive forces are insignificant
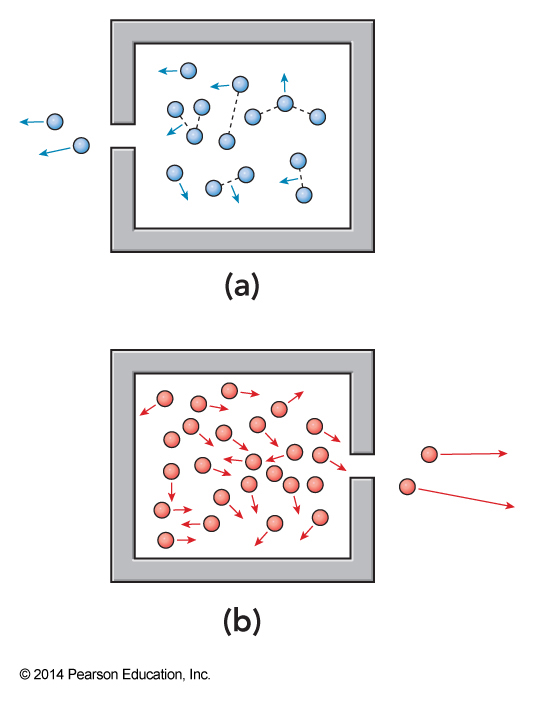
Interesting Expansion Effects
- Methane in compressed tanks cool as it expands through the nozzle
- \(\chem{H_2}\) and \(\chem{He}\), however, have very weak intermolecular forces – \(a\) is very small
- The Joule-Thomson coefficient is negative
- The gases warm as is expands
- The temperature at which the Joule-Thomson coefficient changes sign is called the Joule-Thomson inversion temperature
Example 8.3
Use the van der Waals constants to estimate the Joule-Thomson coefficients for \(\chem{He}\), \(\chem{H_2}\), \(\chem{N_2}\), and \(\chem{CO_2}\) at \(300.\,\mathrm{K}\).
| Substance | \(\alpha\; (\mathrm{L^2\,bar\,mol^{-2}})\) | \(b\; (\mathrm{L\,mol^{-1}})\) | \(C_{Pm}\; (\mathrm{J\,K^{-1}\,mol^{-1}})\) |
|---|---|---|---|
| \(\chem{He}\) | \(2.8\times 10^{-3}\) | \(-0.100\) | \(-0.062\) |
| \(\chem{H_2}\) | \(2.01\times 10^{-2}\) | \(-0.024\) | \(-0.03\) |
| \(\chem{N_2}\) | \(0.110\) | \(0.24\) | \(0.27\) |
| \(\chem{CO_2}\) | \(0.293\) | \(0.675\) | \(1.11\) |
Example 8.4
Given \(a=0.034\,\mathrm{L^2\,bar\,mol^{-2}}\) and \(b=0.0237\,\mathrm{L\,mol^{-1}}\) for \(\chem{He}\), and \(2.25\,\mathrm{L^2\,bar\,mol^{-2}}\) and \(0.0428\,\mathrm{L\,mol^{-1}}\) (respectively) for \(\chem{CH_4}\), calculate the Joule-Thomson inversion temperatures for these gases.
Engines
A Heat Engine
- A heat engine is a device that continuously converts heat into work
- Consider a machine that cycles among \(A \rightarrow B \rightarrow C \rightarrow D \rightarrow A\) $$ w=-\int_A^B P\,dV - \int_B^C P\,dV - \int_C^D P\,dV - \int_D^A P\,dV $$
The Carnot Cycle
- One of the simplest cycles is the Carnot cycle
- Named for Nicolas Carnot
- Developed this first model of the heat engine in 1824
The First of Four Steps of the Carnot Cycle
- Isothermal expansion
- The gas expands isothermally at temperature \(T_{hot}\) from pressure \(P_A\) and volume \(V_A\) to \(P_B\) and \(V_B\)
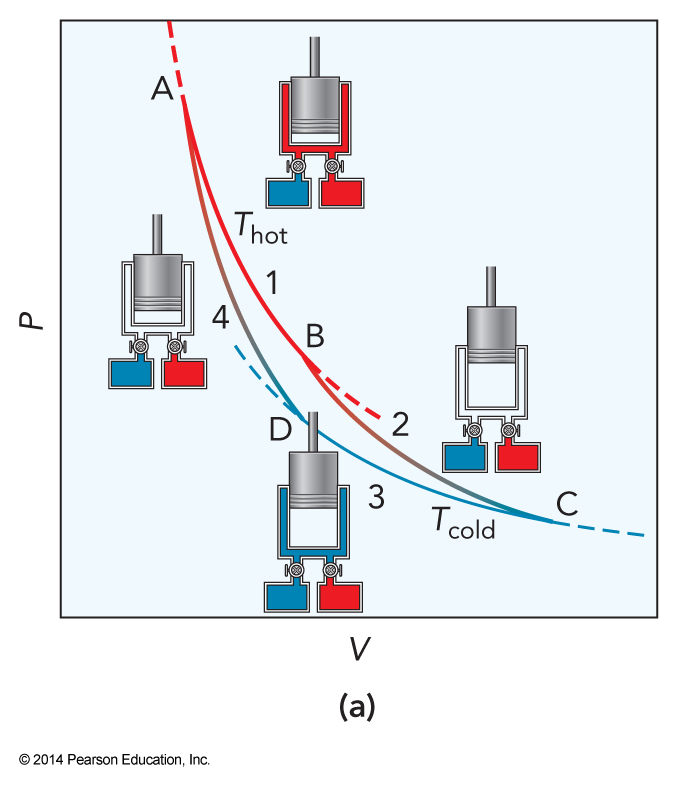
The Second of Four Steps of the Carnot Cycle
- Adiabatic expansion
- Expel the steam
- The system cools
- Expands adiabatically until it reaches \(T_{cold}\) at \(P_C\) and \(V_C\)

The Third of Four Steps of the Carnot Cycle
- Isothermal compression
- The gas is compressed isothermally at temperature \(T_{cold}\) to \(P_D\) and \(V_D\)

The Final of Four Steps of the Carnot Cycle
- Adiabatic compression
- Purge the cold water
- Return to the starting conditions

Step 1: Isothermal Expansion
- First we can work out the work in this step $$ \begin{align} w_1 &= -\int_{V_A}^{V_B} P(V)\,dV = -\int_{V_A}^{V_B} \frac{nRT_{hot}}{V}\,dV \\ &= -nRT_{hot} \ln \frac{V_B}{V_A} \end{align} $$
- Since this is isothermal (and ideal gas) $$ \begin{align} \Delta E(T) &= q+w =0 \\ q_1 &= -w_1 = nRT_{hot} \ln \frac{V_B}{V_A} \end{align} $$
Step 2: Adiabatic Expansion
- For an ideal gas \(\Delta E = C_V\Delta T\)
- For adiabatic process, \(q=0\), so \(\Delta E=w\) $$ \begin{align} w_2 &= C_V(T_{cold}-T_{hot}) \\ q_2 &= 0 \end{align} $$
Step 3: Isothermal Compression
- Analogous to step one, only compression now $$ \begin{align} w_3 &= -\int_{V_C}{V_D} P(V)dV=-nRT_{cold}\ln\frac{V_D}{V_C} \\ q_3 &= nRT_{cold}\ln \frac{V_D}{V_C} \end{align} $$
Step 4: Adiabatic Compression
- Analogous to step 2 $$ \begin{align} w_4 &= -C_V(T_{cold}-T_{hot}) \\ q_4 &= 0 \end{align} $$
Total Work Done
- We can add up all the work done $$ \begin{align} w &= w_1+w_2+w_3+w_4 \\ &= -nR\left(T_{hot}\ln \frac{V_B}{V_A}+T_{cold}\ln \frac{V_D}{V_C}\right) \end{align} $$
- We also know that \(C_V\ln \frac{T_2}{T_1}=-nR\ln\frac{V_2}{V_1}\)
- This means that $$ C_V\ln\frac{T_{hot}}{T_{cold}}=-nR\ln\frac{V_B}{V_C} = -nR\ln\frac{V_A}{V_D} $$
Further Simplification
- We can relate the volume ratios $$ \frac{V_D}{V_A} = \frac{V_C}{V_B} \text{ and } \frac{V_D}{V_C}=\frac{V_A}{V_B} $$
- So the total work is now $$ \begin{align} w &= -nR \left( T_{hot} \ln \frac{V_B}{V_A} + T_{cold} \ln \frac{V_D}{V_C} \right) \\ &= -nR \left( T_{hot} \ln \frac{V_B}{V_A} + T_{cold} \ln \frac{V_A}{V_B} \right) \\ &= -nR \left( T_{hot} - T_{cold} \right) \ln \frac{V_B}{V_A} \\ q &= nR \left( T_{hot} - T_{cold} \right) \ln \frac{V_B}{V_A} \end{align} $$
Efficiency
- The efficiency, \(\varepsilon\), is the ratio of the work obtained to the heat provided by the fuel, \(q_1\) $$ \begin{align} \varepsilon &= -\frac{w}{q_1} = \frac{nR(T_{hot}-T_{cold})\ln \frac{V_B}{V_A}}{nRT_{hot}\ln \frac{V_B}{V_A}} \\ &= \frac{T_{hot}-T_{cold}}{T_{hot}} \end{align} $$
The Otto Cycle
- Idealized version of the operation of an internal combustion engine
- Instead of two temperature reservoirs, we use two material reservoirs
- Fuel supply line
- Exhaust line
- Stesp of the Otto Cycle
- At \(P_A\) and \(T_A\), we ignite the compressed fuel at volume \(V_A\)
- The pressurized combustion products expand adiabatically to \(P_C\) and \(V_C\)
- Piston stop, gas cools isochorically, pressure drops to \(P_D\)
- Adiabatic compression back to \(V_A\)
Otto Cycle Efficiency
- After some math we arrive at an equation for the efficiency of the Otto cycle $$ \begin{align} \varepsilon &= \frac{T_{hot}-T_{cold}}{T_{hot}} \\ &= 1-\left(\frac{V_A}{V_B}\right)^{\frac{C_P-C_V}{C_V}} \end{align} $$
- Note the compression ratio, \(\frac{V_A}{V_B}\)
Maximum Work
- The maximum work is accomplished when the process is reversible
- Therefore, uneven or too rapid combustion reduces the engine’s efficiency
- Combustion rate is a function of the fuel and the igniter
- Adjusting these has long been used to improve engine efficiency
/