Introduction to Thermodynamics: Heat Capacity
Shaun Williams, PhD
The First Law of Thermodynamics
Extensive and Intensive Parameters
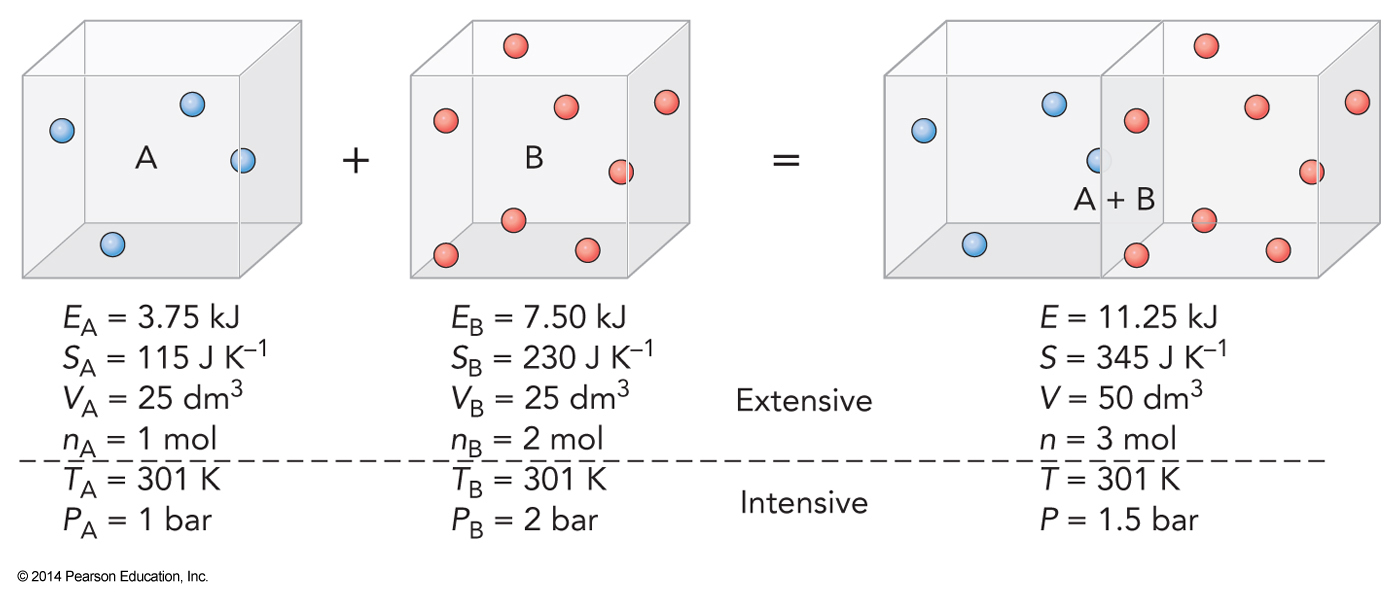
Thermodynamic State
- A single thermodynamic state is a specific set of macroscopic parameters
- Because a thermodynamic state specifies all the parameters, the parameters are called state functions
- Speed is not a state function because that parameter does not describe the entire system
- An equation that expresses one state function in terms of the others is an equation of state
- Equations of State
- Equations like \(P=-\left(\frac{\partial E}{\partial V}\right)_{S,N}\) and \(\left(\frac{\partial E}{\partial S}\right)_{V,N}\equiv T\) give the state function $$ PV=nRT $$
First Law of Thermodynamics
- From our previous discussions we have seen that $$ \dbar q \le T\,dS $$
- The first law of thermodynamics states that $$ \Delta E \equiv E_f - E_i =q+w $$
- If we look at infinitesimal changes in energy $$ dE=\dbar q + \dbar w $$
Inexact Differential, \(\dbar\)
- The inexact differential is used to remind us that \(q\) and \(w\) are not state functions
- They are instead defined by the exact process
- \(q\) and \(w\) do not have a value at any individual point
- To evaluate \(q\) or \(w\), we cannot in principle integrate \(\dbar q\) or \(\dbar w\) directly
- We must replace inexact with exact to integrate
Approximations and Assumptions
Equilibrium
- We will measure the energy of a state where there is no net change in any macroscopic parameter over time
- These are equilibrium states
- Basic thermodynamics has difficulty dealing with non-equilibrium states
Types of Systems
- Closed system – the number and type of molecules is fixed
- Pure – molecules all have the same chemical structure
- Homogeneous – all chemical components in the same phase of matter
- Heterogeneous – more than one phase of matter present
Definitions of Terms Used for Thermodynamics
| System | Meaning |
|---|---|
| Open | May exchange mass and energy with surroundings |
| Closed | All \(n_i\) fixed (no mass exchange and no reactions) |
| Pure | One chemical component (implied unless stated otherwise) |
| Isolated | No mass or energy exchange with surroundings |
| Homogeneous | One phase of matter |
| Heterogeneous | More than one phase of matter |
| Container | Meaning |
| Adiabatic | Walls prevent heat flow |
| Diathermal | Walls allow heat flow |
| Processes | Meaning |
| Quasistatic | System and surroundings always in equilibrium |
| Reversible | System and surroundings at constant total entropy (\(\Delta S_T=0\)) |
| Adiabatic | No heat flow (\(q=0\)) |
| Isentropic | System at constant entropy (\(\Delta S=0\)) |
| Isothermal | System at constant temperature (\(\Delta T=0\)) |
| Isobaric | system at constant pressure (\(\Delta P=0\)) |
| Isochoric | System at constant volume (\(\Delta V=0\)) |
| Isoenergetic | System at constant energy (\(\Delta E=0\)) |
The Standard State
- The standard state is typically labeled with a subscript \(\ominus\)
- Standard state conditions:
- \(1\,\mathrm{bar}=10^5\,\mathrm{Pa} = 0.987\,\mathrm{atm}\)
- Any mixture is separated into its pure components
- Unlike STP, the standard state does not have a specified temperature
Mathematical Tools
Partial Derivatives of Energy
- Pressure: \(P=-\left(\frac{\partial E}{\partial V}\right)_{S,n}\)
- Temperature: \(T=\left(\frac{\partial E}{\partial S}\right)_{V,n}\)
- Chemical potential: \(\mu\equiv \left(\frac{\partial E}{\partial n}\right)_{S,V}\)
The Fundamental Equation
- The fundamental equation is \(E=E(S,V,n_1,\dots,n_k)\)
- Using this and our previous derivative equation and the slope rule for derivatives we come to $$ \begin{align} dE =& \left(\frac{\partial E}{\partial S}\right)_{V,n_1,\dots,n_k} dS + \left(\frac{\partial E}{\partial V}\right)_{S,n_1,\dots,n_k} dV \\ &+ \left(\frac{\partial E}{\partial n_1}\right)_{S,V,n_2,\dots,n_k} dn_1 + \cdots + \left(\frac{\partial E}{\partial n_k}\right)_{S,V,n_1,\dots,n_{k-1}} dn_k \\ =& T\,dS - P\,dV + \mu_1\,dn_1 + \dots + \mu_k dn_k \end{align} $$
Simplifying
- Our differential equation is most convenient when a number of the derivatives on the RHS can be set to zero
- For a closed system, the moles numbers do not change so \(dn_i = 0\)
- This results in closed systems obeying the equation $$ \text{closed system: }dE=T\,dS - P\,dV $$
Legendre Transformation
- We would prefer equations in terms of \(T\) and \(P\) rather than \(S\)
- Let’s say the energy only depends on two extensive variables such that $$ \left(\frac{\partial E}{\partial X_1}\right)_{X_2} = Y_1 \;\; \left(\frac{\partial E}{\partial X_2}\right)_{X_1}=Y_2 $$
- The partial Legendre transform of energy with respect to \(X_1\) switches the functional dependence to \(Y_1\) $$ Z(Y_1,X_2)=E(X_1,X_2)-X_1Y_1 $$ $$ \left(\frac{\partial E}{\partial Y_1}\right)_{X_2} = -X_1 \;\; \left(\frac{\partial E}{\partial X_2}\right)_{Y_1}=Y_2 $$
- Doing some differential math we arrive at $$ dZ=-X_1\,dY_1 + Y_2\, dX_2 $$
Legendre Transforms - Thermodynamic Potentials
- The enthalpy, \(H\), transform of \(E\) with respect to \(V\) $$ H(S,P,n_1,\dots,n_k) = E+PV $$
- The Helmholtz free energy, \(F\), transform of \(E\) with respect to \(S\) $$ F(T,V,n_1,\dots,n_k) = E-TS $$
- The Gibbs free energy, \(G\), transform of \(E\) with respect to \(V\) and \(S\) $$ G(T,P,n_1,\dots,n_k) = E-TS+PV = H-TS $$
Derivatives From the Thermodynamic Potentials
- From the thermodynamic potentials we can define some useful derivative equations $$ \begin{align} dE &= T\, dS - P\, dV + \mu_1\, dn_1 + \cdots + \mu_k\, dn_k \\ dH &= T\, dS + V\, dP + \mu_1\, dn_1 + \cdots + \mu_k\, dn_k \\ dF &= -S\, dT - P\, dV + \mu_1\, dn_1 + \cdots + \mu_k\, dn_k \\ dG &= -S\, dT + V\, dP + \mu_1\, dn_1 + \cdots + \mu_k\, dn_k \end{align} $$
Closed System Example
- In a closed system in contact with a temperature and pressure reservoir (fixes \(T\) and \(P\)) the entropy change is $$ \begin{align} T\,dS &= dE+P\,dV \\ dS &= \frac{1}{T} \left(dE+P\,dV\right) \\ dS &= \frac{dH}{T} \end{align} $$
Mixed Second Derivatives
$$ \begin{align} \left[ \frac{\partial}{\partial V} \left( \frac{\partial E}{\partial S} \right)_{V,n} \right]_{S,n} &= \left[ \frac{\partial}{\partial S} \left( \frac{\partial E}{\partial V} \right)_{S,n} \right]_{V,n} = \left( \frac{\partial T}{\partial V} \right)_{S,n} \\ \left[ \frac{\partial}{\partial S} \left( \frac{\partial E}{\partial V} \right)_{S,n} \right]_{V,n} &= -\left( \frac{\partial P}{\partial S} \right)_{V,n} \\ \end{align} $$
- The order of when you take the two derivatives so these expressions are the same $$ \begin{align} \left[ \frac{\partial}{\partial V} \left( \frac{\partial E}{\partial S} \right)_{V,n} \right]_{S,n} &= \left[ \frac{\partial}{\partial S} \left( \frac{\partial E}{\partial V} \right)_{S,n} \right]_{V,n} \\ \left( \frac{\partial T}{\partial V} \right)_{S,n} &= -\left( \frac{\partial P}{\partial S} \right)_{V,n} \end{align} $$
- This is one of the set of Maxwell Relations
Maxwell Relations
- Relating the results of mixed second derivatives yield the Maxwell Relations $$ \begin{align} \left( \frac{\partial T}{\partial V} \right)_{S,n} &= -\left( \frac{\partial P}{\partial S} \right)_{V,n} \\ \left( \frac{\partial T}{\partial P} \right)_{S,n} &= \left( \frac{\partial V}{\partial S} \right)_{P,n} \\ \left( \frac{\partial S}{\partial V} \right)_{T,n} &= \left( \frac{\partial P}{\partial T} \right)_{V,n} \\ \left( \frac{\partial S}{\partial P} \right)_{T,n} &= -\left( \frac{\partial V}{\partial T} \right)_{P,n} \end{align} $$
Volume Scaled Derivatives
- Some volume scaled derivatives are tabulated
- Isobaric coefficient of thermal expansion $$ \alpha \equiv \frac{1}{V}\left( \frac{\partial V}{\partial T}\right)_{P,n} $$
- Isothermal compressibility $$ \kappa_T \equiv -\frac{1}{V} \left( \frac{\partial V}{\partial P} \right)_{T,n} $$
- Adiabatic compressibility $$ \kappa_S \equiv -\frac{1}{V} \left( \frac{\partial V}{\partial P}\right)_{S,n} $$
Partition Functions
- We know that $$ \begin{align} q_\chem{rot} &= \frac{k_\mathrm{B}T}{B} \;\; q_\chem{vib} = \left[ 1-e^{-\frac{\omega_e}{k_\mathrm{B}T}}\right]^{-1} \\ Q(T) &= q_\chem{elec}(T)q_\chem{vib}(T)q_\chem{rot}(T)Q_\chem{trans}(T) \end{align} $$
- The internal energy can be defined in terms of the partition function, as we have learned $$ E=k_\mathrm{B}T^2\left( \frac{\partial \ln Q(T)}{\partial T}\right)_{V,n} $$
The Entropy
$$ \begin{align} \frac{E}{k_\mathrm{B}T} &= \ln \Omega - \ln Q(T) \\ k_\mathrm{B} \ln \Omega &= k_\mathrm{B} \ln Q(T) + \frac{E}{T} \\ S &= k_\mathrm{B} \ln Q(T) + k_\mathrm{B}T \left( \frac{\partial \ln Q(T)}{\partial T}\right)_{V,n} \end{align} $$
The Helmholtz Energy
$$ \begin{align} F =& E-TS \\ =& k_\mathrm{B}T^2 \left(\frac{\partial \ln Q(T)}{\partial T}\right)_{V,n} \\ & -T\left[ k_\mathrm{B} \ln Q(T) + k_\mathrm{B}T\left(\frac{\partial \ln Q(T)}{\partial T}\right)_{V,n} \right] \\ F =& -k_\mathrm{B}T \ln Q(T) \end{align} $$
The Pressure and the Chemical Potential
$$ \begin{align} P &= -\left( \frac{\partial F}{\partial V}\right)_{T,n} = k_\mathrm{B}T \left(\frac{\partial \ln Q}{\partial V}\right)_{T,n} \\ \mu &= \left(\frac{\partial F}{\partial n}\right)_{T,V} = -k_\mathrm{B}T \left(\frac{\partial \ln Q}{\partial n}\right)_{T,V} \end{align} $$
Heat Capacities
Heat Capacity
- Heat capacity quantifies the amount of energy we must add to a sample to change its temperature by a certain amount
- Effectively it is the flow of heat per unit change in temperature \(C(T)\equiv \frac{\dbar q}{dT}\)
- Molar heat capacity is an intensive rather than extensive property $$ C_m(T) \equiv \frac{1}{n} C(T) = \frac{1}{n} \frac{\dbar q}{dT} $$
Measuring Heat Capacities
- We can measure the heat capacity under various conditions
- When measured under constant pressure conditions we get \(C_P\)
- When measured under constant volume conditions we get \(C_V\)
- \(C_P\) is the most commonly tabulated form of heat capacity.
Different Types of Work
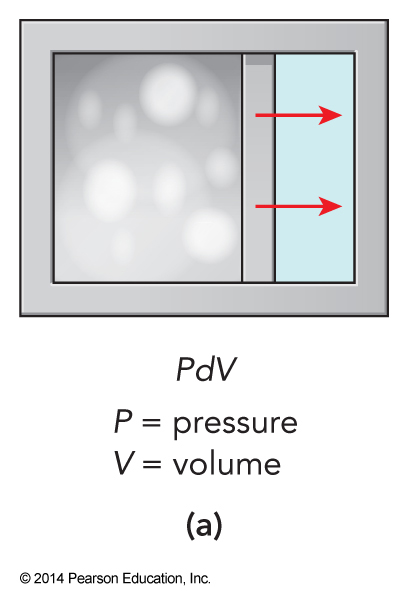
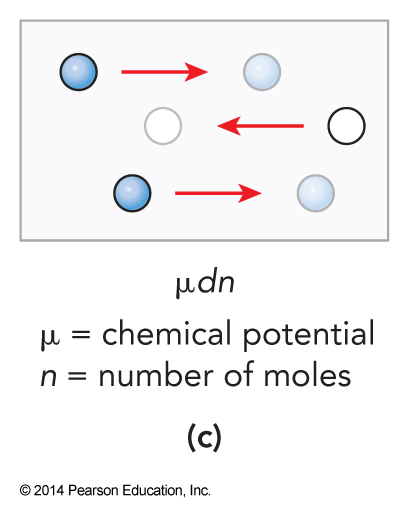
More on Heat Capacities
- \(C\) measures an incremental change in one form of transferred energy
- Incremental change in energy of a closed system can be written as \(dE=T\,dS-P\,dV = \dbar q + \dbar e\)
- Changes in volume are usually associated with work
- The most straightforward work is the mechanical energy expended or absorbed as a sample expands or contracts, called \(PV\) work
\(PV\) Work
- If only \(PV\) work, then the incremental \(\dbar w\) is the change in energy due to the incremental expansion or contraction \(\dbar w = -P_\chem{min}\,dV\)
- For reversible process, we change the volume so slowly that the pressure on both sides of the boundary are always equal to within our ability to measure the difference, therefore \(\dbar w = -P\,dV\) $$ \dbar q_\chem{rev} = dE-\dbar w_\chem{rev} = T\,dS-P\,dV-(-P\,dV) = T\,dS $$
Without \(PV\) Work
$$ \begin{align} \left(\frac{\partial E}{\partial T}\right)_{V,n} &= \left( \frac{T\partial S - P\partial V}{\partial T}\right)_{V,n} \\ &= \left(\frac{T\partial S}{\partial T}\right)_{V,n} \\ &= \left(\frac{\dbar q}{dT}\right)_{V,n} \\ &= C_V(T) \\ \text{So: }& C_V(T)=\left(\frac{\partial E}{\partial T}\right)_{V} \end{align} $$
For an Ideal Gas
- We know that \(E=\frac{1}{2}N_{ep}NK_\mathrm{B}T=\frac{1}{2}N_{ep}nRT\)
- \(N_{ep}\) is the number of equipartition degrees of freedom in translation, rotation, and vibration
- Using our new \(C_V\) equation we can find that $$ C_V=\left(\frac{\partial E}{\partial T}\right)_V=\frac{1}{2}N_{ep}nR\left(\frac{\partial T}{\partial T}\right)_V = \frac{1}{2}N_{ep}nR $$
- For monatomic gas, \(N_{ep}=3\) so \(C_V=\frac{3}{2}nR\)
Example 7.1
You have a constant-volume sample with a known quantity of mercury gas, a thermometer, and a calorimeter that allows you to add or remove measured amounts of energy from the sample. How could you use this apparatus to determine whether gas-phase mercury was in monatomic or diatomic form, that is, \(\chem{Hg(g)}\) or \(\chem{Hg_2(g)}\)? What numerical results would you look for in your measurements?
Constant Pressure Heat Capacity
- We can begin with enthalpy $$ dH=T\,dS + V\,dP + \mu\,dn $$
- For a closed sample at constant pressure, we set \(dP\) and \(dn\) to zero
- Recalling that \(H=E+PV\) we find that $$ dH=dE+P\,dV + V\,dP = \dbar q + \dbar w + P\,dV + V\,dP $$
- So at constant pressure if \(dw=-P\,dV\), \(dH=\dbar q\) $$ C_P \equiv \left(\frac{\partial q_\chem{rev}}{\partial T}\right)_P = \left(\frac{\partial H}{\partial T}\right)_P $$
Heating at Constant Pressure vs Constant Volume
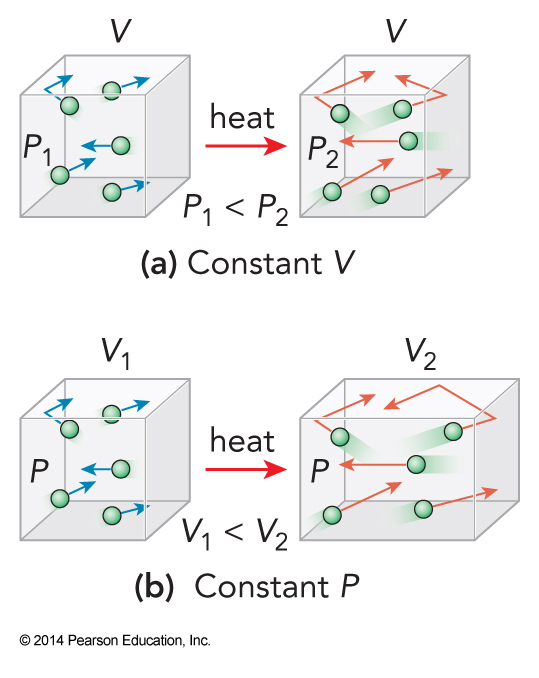
How Are \(C_P\) and \(C_V\) Related?
- Start with enthalpy \(H=E+PV\)
- Now we expand our expression for \(C_P\) $$ C_P=\left(\frac{\partial (E+PV)}{\partial T}\right)_P=\left(\frac{\partial E}{\partial T}\right)_P + P\left(\frac{\partial V}{\partial T}\right)_P $$
- We can use a calculus identity $$ \begin{align} \left(\frac{\partial X}{\partial Y}\right)_Z &= \left(\frac{\partial X}{\partial Y}\right)_W + \left(\frac{\partial X}{\partial W}\right)_Y \left(\frac{\partial W}{\partial Y}\right)_Z \\ \left(\frac{\partial E}{\partial T}\right)_P &= \left(\frac{\partial E}{\partial T}\right)_V+\left(\frac{\partial E}{\partial V}\right)_T\left(\frac{\partial V}{\partial T}\right)_P \end{align} $$
How are \(C_P\) and \(C_V\) Related?
- We can now rewrite our equation $$ C_P = \left(\frac{\partial E}{\partial T}\right)_V+\left(\frac{\partial E}{\partial V}\right)_T\left(\frac{\partial V}{\partial T}\right)_P+P\left(\frac{\partial V}{\partial T}\right)_P $$
- The first term is \(C_V\)
- The second term is called the internal pressure
- Using our definition of the coefficient of thermal expansion $$ \begin{align} C_P &= C_V + V\alpha \left[ \left(\frac{\partial E}{\partial T}\right)_T+P\right] \\ C_{Pm} &= C_{Vm} + V_m \alpha \left[ \left(\frac{\partial E}{\partial T}\right)_T+P\right] \end{align} $$
Ideal Gas
- The coefficient of thermal expansion of an ideal gas is $$ \alpha=\frac{1}{V}\left(\frac{\partial V}{\partial T}\right)_P = \frac{1}{V}\left[\frac{\partial}{\partial V} \left(\frac{nRT}{P}\right)\right]_P = \frac{nR}{PV} = \frac{1}{T} $$
- The ideal gas constant pressure heat capacity is therefore \(C_P=C_V+V\alpha P=C_V+nR\)
Example 7.2
Use the definition of the coefficient of thermal expansion to find the relationship between \(C_P\) and \(C_V\) at the temperature at maximum density (TMD) for any substance.
Heat Capacities and Real Gases
- The general relationship between the heat and the temperature change is $$ q=\int_{T_1}^{T_2}\dbar q = \int_{T_1}^{T_2}\frac{\dbar q}{dT}dT=\int_{T_1}^{T_2}C(T)\,dT $$
- If we assume that the heat capacity does not depend on temperature $$ q=\int_{T_1}^{T_2} C\,dT=C\int_{T_1}^{T_2}dT=C\Delta T $$
Heat Capacities of Several Substances
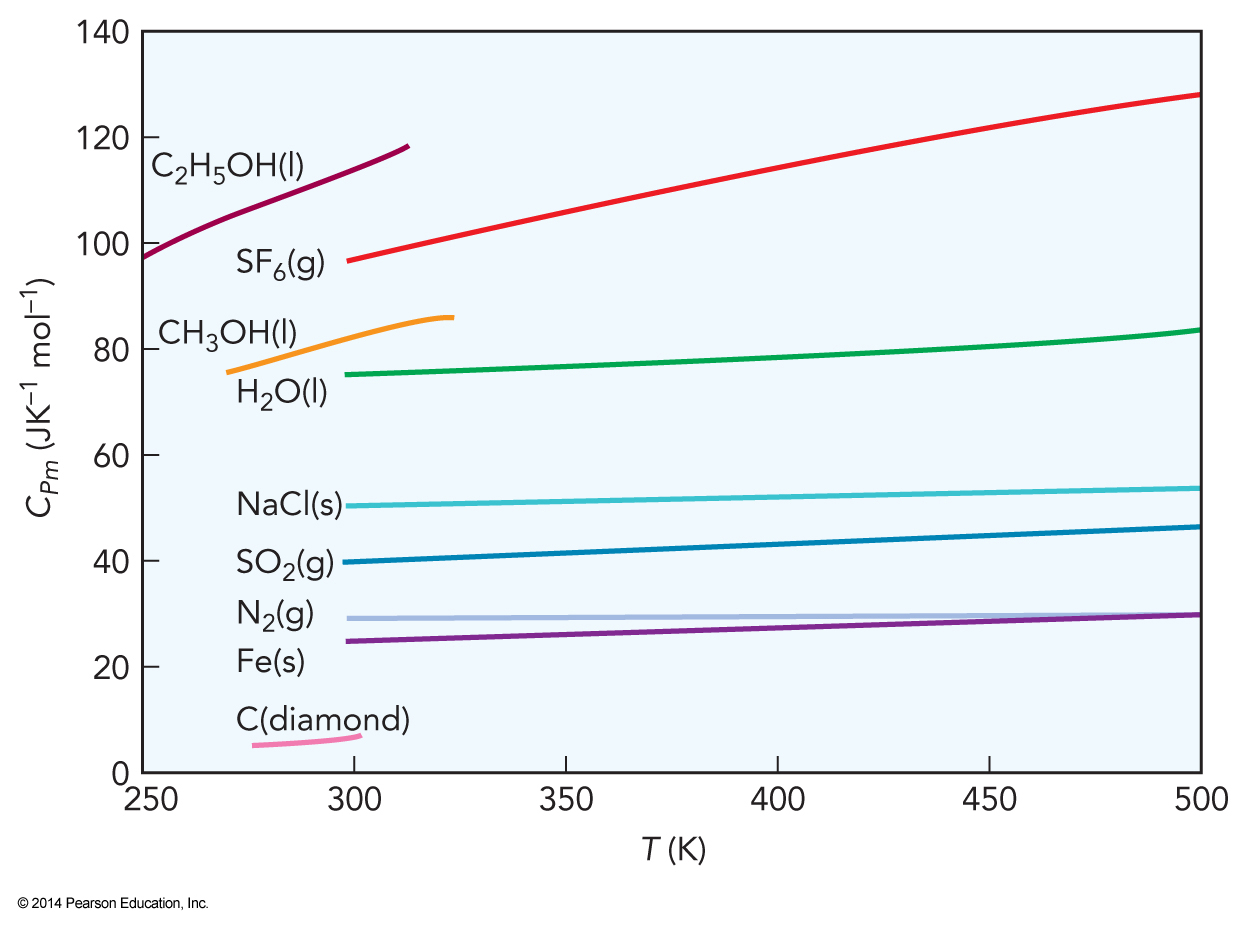
More on Heat Capacities of Real Gases
- Heat capacities for gas-phase atoms tend to lie very close to the equipartition value
- The more atoms in the molecule, the more the equipartition heat capacity overestimates the experimental heat capacity
- Heat capacities for diatomics and triatomics are more accurately predicted by full equipartition when the atoms are heavier
- A lower limit to the heat capacity can therefore be estimated by neglecting all the vibrations
Example 7.3
The molar heat capacity at constant pressure of \(\chem{CCl_4}\) is \(83.30\,\mathrm{J\,K^{-1}\,mol^{-1}}\) at \(298\,\mathrm{K}\). If we heated a \(1.00\,\mathrm{mol}\) sample of \(\chem{CCl_4}\) gas with \(1.00\,\mathrm{J}\), starting near \(298\,\mathrm{K}\), roughly what percent of the heat would go into rotation, and what percent into vibration? Assume that the temperature change is small enough that the heat capacity may be treated as constant.
For a Linear Diatomic Molecule
- After a lot of math we can arrive at an equation for the constant pressure heat capacity in terms of vibrational frequency $$ C_{Pm} = \frac{7}{2}R+\left(\frac{\omega_e}{k_\mathrm{B}T}\right)^2 \left\{ \begin{split} & e^{-\frac{\omega_e}{k_\mathrm{B}T}}\left[1-2e^{-\frac{\omega_e}{k_\mathrm{B}T}}\right] \\ & +e^{-\frac{2\omega_e}{k_\mathrm{B}T}}\left[4-6e^{-\frac{\omega_e}{k_\mathrm{B}T}}\right] \\ &+\cdots \end{split} \right\} R $$
Example 7.4
The vibrational constant of \(\chem{{}^{35}Cl_2}\) is \(560.5\,\mathrm{cm^{-1}}\). Estimate the value of \(C_{Pm}\) for \(\chem{{}^{35}Cl_2}\) at \(298.15\,\mathrm{K}\).
Idealized Solid
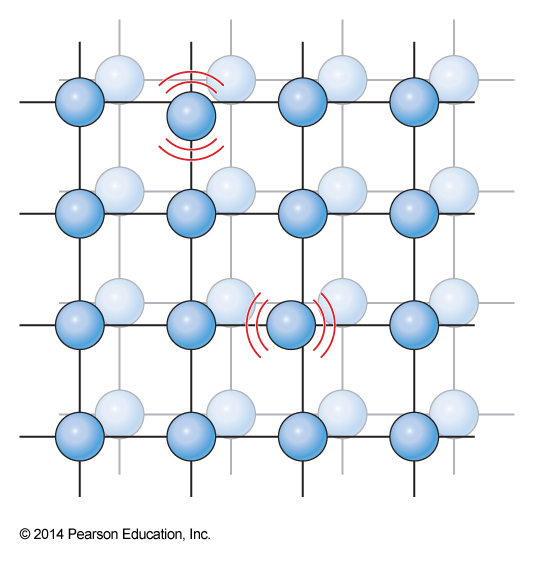
Einstein Solid
- Albert Einstein derived the heat capacity for an idealized crystal, called the Einstein solid
- He treated each particle as an independent harmonic oscillator
- Einstein postulated that he could find the value ε by assuming some single effective vibrational constant \(\omega_E\) $$ q_\chem{vib}(T,V) = \frac{1}{1-e^{-\frac{\omega_E}{k_\mathrm{B}T}}} $$
The Einstein Heat Capacity
- If we assume that each atom vibrates as an independent harmonic oscillator $$ E_m = 3\mathcal{N}_\mathrm{A} \expect{\varepsilon}_\chem{vib} = \frac{3\mathcal{N}_\mathrm{A}\omega_E}{e^{\frac{\omega_E}{k_\mathrm{B}T}}-1} $$
- From this we can derive the constant volume molar heat capacity $$ C_{Vm} = \frac{3\mathcal{N}_\mathrm{A}\omega_e^2e^{\frac{\omega_e}{k_\mathrm{B}T}}}{k_\mathrm{B}T^2\left(e^{\frac{\omega_e}{k_\mathrm{B}T}}-1\right)^2} $$
Success of the Einstein Solid
- At high temperatures, the heat capacity predicted by the Einstein solid is usually close to experimental
- When the solid is cooled, the individual stretches no longer can be excited and the heat capacity becomes radically different
- At cold temperature, the vibrations are dominated by low-frequency, collective motions of the atoms called phonon modes
Phonon Modes in Crystals
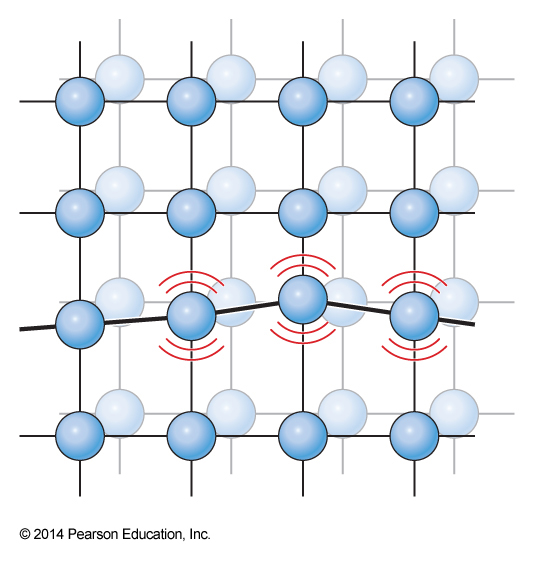
Debye Heat Capacity
- The Debye heat capacity improves on the Einstein solid by taking collective motions into account
- Debye argued that the density of quantum states \(W\) for these oscillations goes as (\(A\) is a normalization constant) $$ W(\omega)\,d\omega = AV\omega^2\,d\omega $$ $$ A=\frac{9N}{\omega_D^2V} $$
The Debye Heat Capacity Equation
- Without doing all the calculus, we can find that $$ \begin{align} E_m &\approx \frac{3\pi^4 \mathcal{N}_\mathrm{A} k_\mathrm{B}^4T^4}{5\omega_D^3} \\ C_{Vm} &= \left( \frac{\partial E_m}{\partial T}\right)_V \approx \frac{12\pi^4\mathcal{N}_\mathrm{A}k_\mathrm{B}^4T^3}{5\omega_D^3} \end{align} $$
Comparison of Heat Capacities
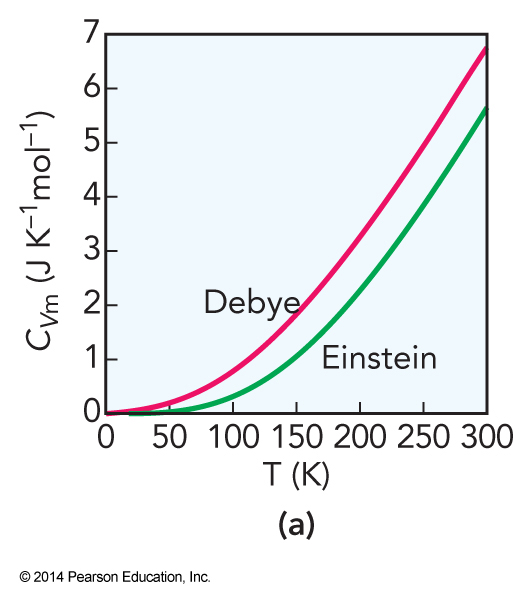
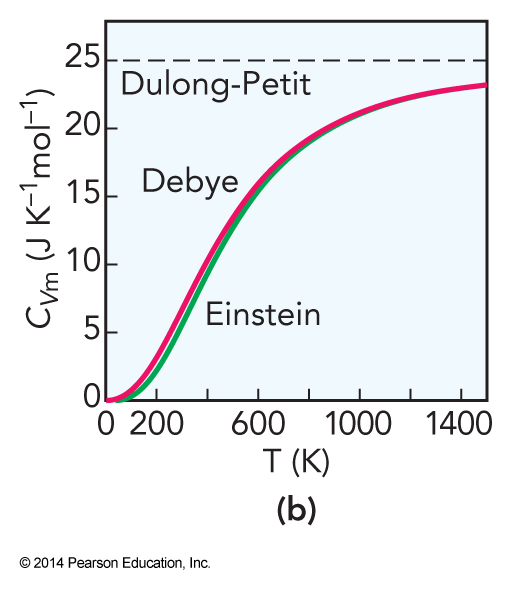
Specific Heat Capacities
- It is often easier to measure the mass of liquids and solids compared to gases
- This means that we can put the heat capacities of solids and liquids on a per gram basis rather than a per mole basis
- Heat capacities per gram are called specific heat capacities and designated with a lower case c
Heat Capacities of Selected Solids
| Solid | \(\mathcal{M} \\ (\mathrm{g\,mol^{-1}})\) | \(C_{Pm} \\ (\mathrm{J\,K^{-1}\,mol^{-1}})\) | \(c_{P} \\ (\mathrm{J\,K^{-1}\,g^{-1}})\) | Solid | \(c_{P} \\ (\mathrm{J\,K^{-1}\,g^{-1}})\) |
|---|---|---|---|---|---|
| Lithium | 6.94 | 24.8 | 0.516 | Hematite | |
| Beryllium | 9.01 | 16.4 | 0.113 | Pyrex glass | 0.84 |
| Carbon (graphite) | 12.01 | 8.53 | 0.059 | Gypsum | 1.09 |
| Carbon (diamond) | 12.01 | 6.11 | 0.043 | Loose wool | 1.26 |
| Sodium | 22.99 | 28.2 | 1.23 | Paper | 1.34 |
| Silicon | 28.09 | 20.0 | 0.75 | White pine | 2.5 |
| Sulfur | 32.07 | 22.6 | 0.71 | Paraffin wax | 2.9 |
| Arsenic | 74.92 | 24.6 | 0.33 | ||
| Tantalum | 180.9 | 25.4 | 0.14 | ||
| Uranium | 238.0 | 27.7 | 0.12 |
Heat Capacities of Monatomic Liquids
- We can define the heat capacities in terms of the pair correlation function, \(\mathcal{G}(R)\) $$ \begin{align} C_{Vm} &= \frac{3R}{2} + 2\pi \mathcal{N}_\mathrm{A}^2\left(\frac{\rho_m}{\mathcal{M}}\right)\int_0^\infty u(R) \left( \frac{\partial \mathcal{G}(R)}{\partial T}\right)_V R^2\,dR \\ &\approx \frac{3R}{2}+\left(\frac{2\pi \mathcal{N}_\mathrm{A}^2}{k_\mathrm{B}T}\right)\left(\frac{\rho_m}{\mathcal{M}}\right)\left\{ \frac{304\varepsilon^2R_\chem{LJ}^3}{315}\right\} \\ &\approx \frac{3R}{2} + \left(2\pi \mathcal{N}_\mathrm{A}k_\mathrm{B}R_\chem{LJ}^3\right)\left(\frac{\rho_m}{\mathcal{M}}\right) \\ &\approx \frac{3R}{2}+\left(\frac{3Rb\rho_m}{\mathcal{M}}\right)=3R\left(\frac{1}{2}+\frac{b\rho_m}{\mathcal{M}}\right) \end{align} $$
Molar Heat Capacities of Simple Liquids and Gases
| Substance | \(T_b \\ (\mathrm{K})\) | \(C_{Vm}\mathrm{(liq)} \\ (\mathrm{J\, K^{-1}\, mol^{-1}})\) | \(C_{Vm}\mathrm{(gas)} \\ (\mathrm{J\, K^{-1}\, mol^{-1}})\) | \(\text{Difference} \\ (\mathrm{J\, K^{-1}\, mol^{-1}})\) |
|---|---|---|---|---|
| \(\chem{N_2}\) | 77.4 | 54.5 | 29.3 | 25.2 |
| \(\chem{Ar}\) | 87.3 | 40.6 | 14.5 | 26.1 |
| \(\chem{CH_4}\) | 111.7 | 51.6 | 27.3 | 24.3 |
| \(\chem{Xe}\) | 165.1 | 37.3 | 12.4 | 24.9 |
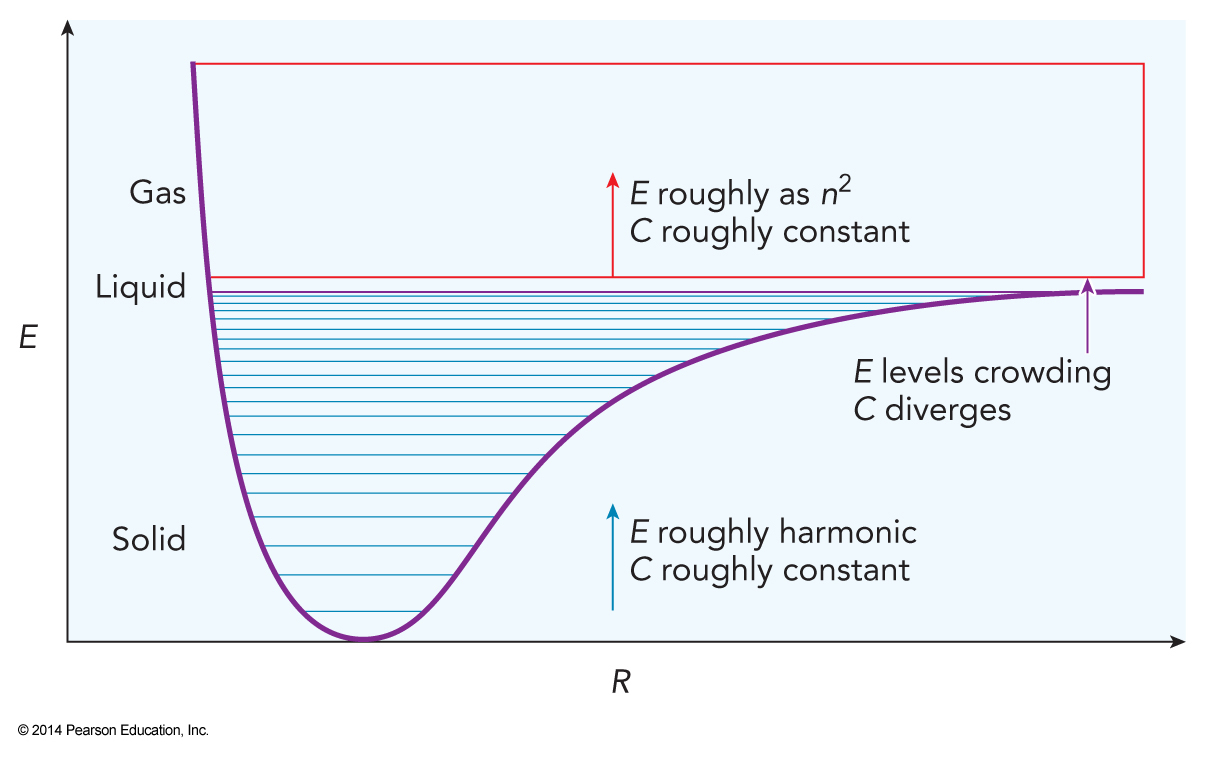
Population of Different Phases in the Potential
/