Classical Physical Chemistry Sets the Stage
Shaun Williams, PhD
The Classical Properties of Matter
What do we measure?
- We measure few things directly
- We can directly measure time and distance
- How do we measure mass?
- By how far a spring in a scale is compressed
- How do we measure temperature?
- By how far the mercury rises
Which is ice and which is diamond?
- By observation they appear the same
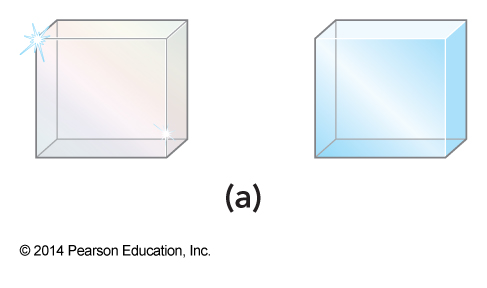
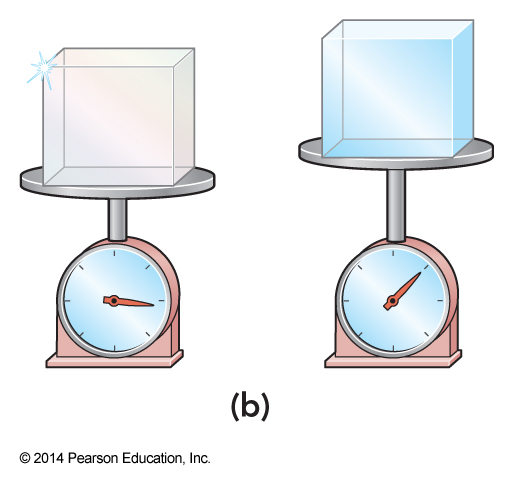
Which is ice and which is diamond? Can we tell by mass?
- For equal volumes of each, the two substances will compress the spring different amounts
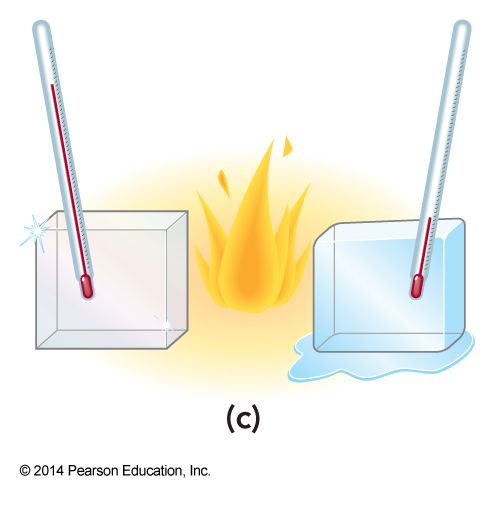
Which is ice and which is diamond? Can we tell by heating the samples?
- The ice will melt at a lower temperature.
Classical Parameters - Volume
- Everything occupies three dimensions in space
- We can measure the distance occupied along each coordinate axis to determine the volume
- SI unit of volume is m3
- Good for buildings and bulldozers
- Bad for laboratory measurements
- \( 1\,\mathrm{L}\equiv 10^{-3}\,\mathrm{m}^3 \) and \( 1\,\mathrm{mL} = 1\,\mathrm{cm}^3 = 10^{-6}\,\mathrm{m}^3 \)
Classical Parameters - Mass and Moles
- Classical chemistry established that atoms of the same element share the same (or nearly the same) mass
- Relation of mass of a substance to number of particles is the mole (defined by Avogadro's number) \( 1\,\mathrm{mol} = 6.022\times 10^{23} \)
- Number of moles of particles of mass \( M \) is \( n=\frac{M}{\mathcal{M}} \)
- \( \mathcal{M} \) is the molar mass (\( \mathrm{g}\,\mathrm{mol}^{-1} \))
Classical Parameters - Pressure
- Explanation of how matter changes requires force
- Force is proportional to the application area
- Measuring a system's pressure will provide the force by \( P=\frac{F}{A} \)
- SI unit: Pascal (Pa)
- \( 1\,\mathrm{bar} = 10^5\,\mathrm{Pa} \)
- \( 1\,\mathrm{bar} \) is about 2% of typical atmoshperic pressure at sea level
Classical Parameters - Temperature
- Usually related to the average speed of particles
- If ice is surrounded by air, the air molecules are traveling faster than the ice molecules
- Collision between the faster air molecules with the ice molecules transfers energy to the ice, thereby warming it up
Measuring Temperature
- Temperature was first measured by its ability to cause mercury to expand
- Or to alter the voltage in of certain circuit components
- Typically we use Celsius scale in the lab
- In P Chem we nearly always use Kelvin where $$ T(\mathrm{K}) = T(^\circ \mathrm{C}) + 273.15 $$
- This is also called the absolute temperature scale
Thermodynamics
What is thermodynamics?
- Thermodynamics is the study of the conversion of energy among different forms and the transfer of energy between different systems
- Chemists are interested in molecular structure and how to change it
- They merge in chemical thermodynamics
- Probe the flow of energy during the transformation of reactants to products
Energy
- Energy is divided into three classes
- Kinetic
- Potential
- Radiant
- Energy is the capacity to apply a force or (equivalently) to oppose an existing force
- In this course we will neglect the conversion of mass into energy
Zero Energy
- The minimum possible energy at which all the particles in the system are
- Fully assembled
- Present in whatever container we have constructed for them
- This energy is called internal energy of the system
- Experimental properties typically only measure changes in energy, \( \Delta E = E_f - E_i \)
The First Law
- Divides the change of energy into two contributions
- Work, \(w\), is the energy change that drives a net shift in the distribution of mass in the system
- Heat, \(q\), is any other energy change – in particular the energy associated with changes in the random motions of the individual particles in the system
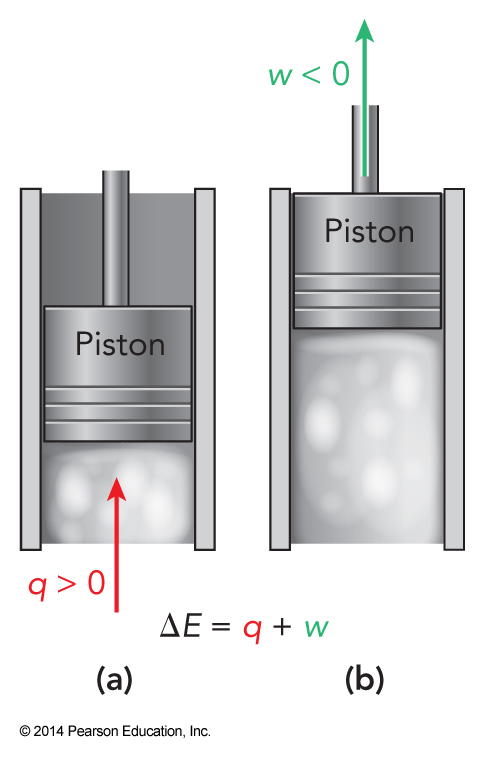
- Mathematically: \( \Delta E \equiv E_f-E_i =q+w \)
Signs
- For work, \(w\)
- Positive work means work is done to the system, increasing the samples energy
- Negative work means work is done by the system
- For heat, \(q\)
- Positive heat means heat is entering the system
- Negative heat means heat is leaving the system
First Law Graphically
A Steam Example
- Let’s say we want to get work out of the steam in a pipe might want to raise the temperature of the steam by heating the pipe
- Some of that energy would instead by diverted into expanding the volume of the gas a piston at one end of the pipe
- If we calculate \(\Delta E\), we need to include the heating of the gas and the work done by the expansion
A Steam Example, Signs
- The gas is heated so \(q\) is positive (heat is entering the system)
- The gas does work so \(w\) is negative
- Therefore, the total change in energy, \(\Delta E\), is less than the energy needed to heat the steam $$ \Delta E = q+w < q $$
- Because of this difference, we calculate the change in a new variable called enthalpy, \(H\)
Enthalpy
- At constant pressure, \(\Delta H=q\)
- If the pressure changes then the energy needed to do the work changes and then enthalpy isn’t valid
Back to the steam pipe
- Some of the input energy goes into warming the piston rather than pushing it forward
- Josiah Willard Gibbs invented a way of looking at systems, leading to the Gibbs free energy, \(G\)
- Gibbs and others found a way to define the maximum amount of work obtainable other than by expansion
- Defined at constant temperature and pressure
Blocks of diamond and ice
- Add energy - the diamond’s temperature increases
- Add energy – the ice’s temperature stays the same as long as there is both water and ice
- Clearly, energy and temperature are not the same phenomenon
- There is clearly some other variable that connects energy and temperature
Entropy and the Second Law
- Rudolf Clausius formulated a relationship between heat and temperature
- Based on a new parameter he called entropy
- Clausius realized that the heat used to drive an engine is always greater than the useful work the engine could do
- The difference between input heat and the work done as a heat transfer to the surroundings, \(q_{surr}\)
An engine
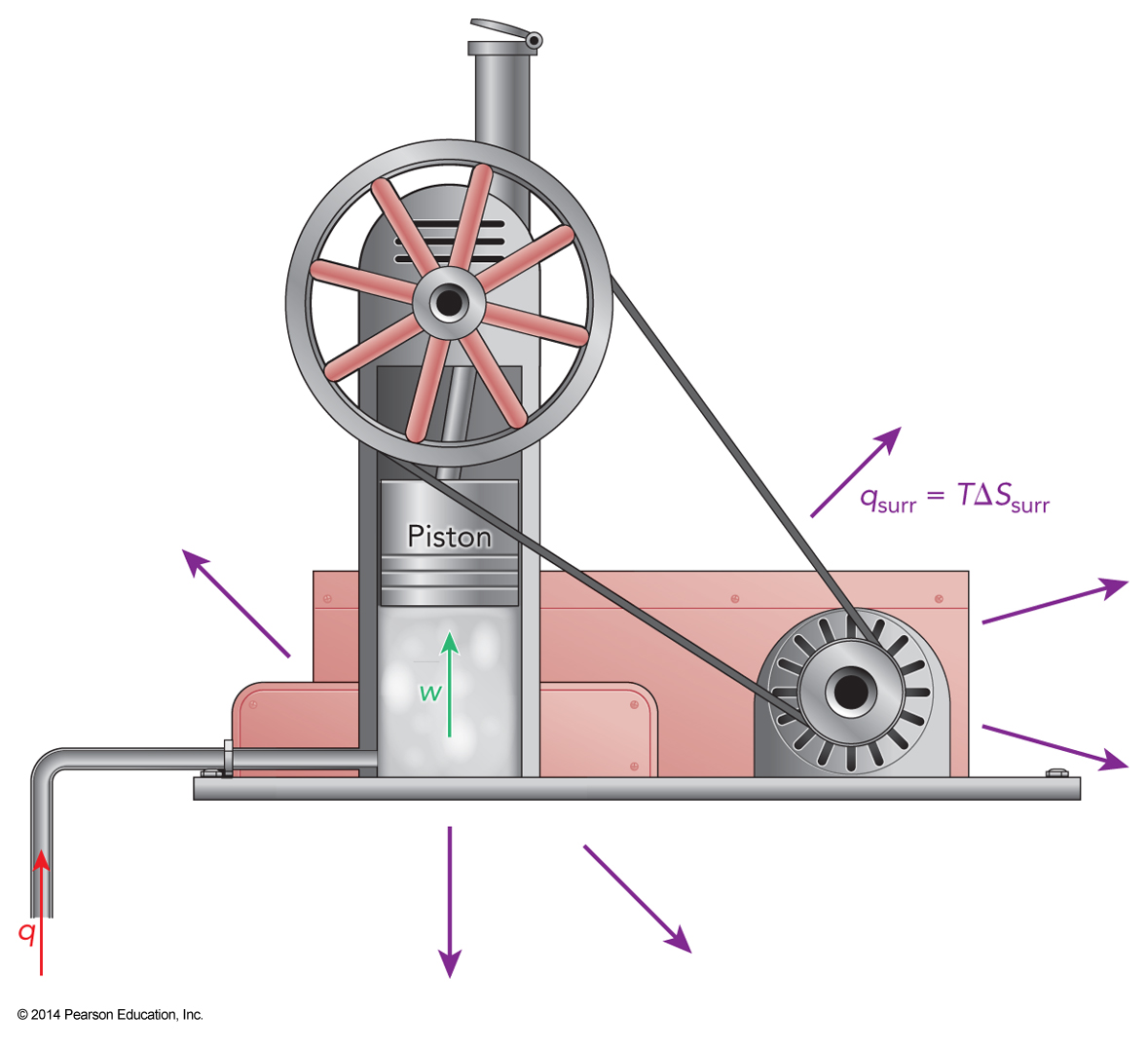
Defining Entropy
- Lost energy tends to grow in proportion to the operating temperature
- Clausius defined entropy, \(S\), as $$ \Delta S_{surr} = \int \frac{q_{surr}}{T} $$
- \(\Delta S_{surr}\) is the change in entropy of the surroundings
- After a complete cycle, an engine would be in its initial state but the surroundings would be warmer
Alternative Entropy Definition
- Entropy is central to thermodynamics
- It explains how temperature and energy are different
- Clausius defined entropy in terms of the independent variable temperature
- Alternatively we can let entropy be independent $$ T \equiv \left( \frac{\partial E}{\partial S} \right)_{V,n} $$
Explanation
- Understanding $$ T \equiv \left( \frac{\partial E}{\partial S} \right)_{V,n} $$
- \(\partial \) is like a tiny \(\Delta\)
- So we have a tiny (infinitesimal) change in energy on top
- On the bottom is a tiny change in entropy
- Ratio these two tiny changes
- This ratio is temperature when the volume and number of moles are held constant
Melting Ice
$$ T\equiv \left( \frac{\partial E}{\partial S} \right)_{V,n} $$
- As we begin heating the ice, the energy rises much faster than the entropy
- The equation tells us that this means \(T\) is rising
- At the melting point, suddenly the energy and entropy are rising at the same rate
- The equation tells us that this means \(T\) is not changing
Another Clausius realization
- From numerous measurements, Clausius realized that \(\Delta S_T \ge 0 \)
- The change in the total (overall) entropy can never increase
- \(\Delta S_T=0\) is reserved for an ideal case called a reversible process
- Basically this means that there is always some inefficiency in real systems
The Kinetic Theory of Ideal Gases
Towards our modern molecular theory of matter
- The kinetic theory of gases imagined that gases are
- Independent particles
- Randomly moving
- Ideal gas is a system of point masses that interact with only the walls of the container
- Interactions with the walls are purely elastic collisions
The Maxwell-Boltzmann Distribution
- James Clerk Maxwell began with the idea that molecular motions are random
- Work by botanist Robert Brown – pollen particles in water
- Results of random events tend to cluster around an average
Example: Flipping 50 coins
- About 11% of the time we actually get the average
- Less probability away from the average
- This is holds for all random events
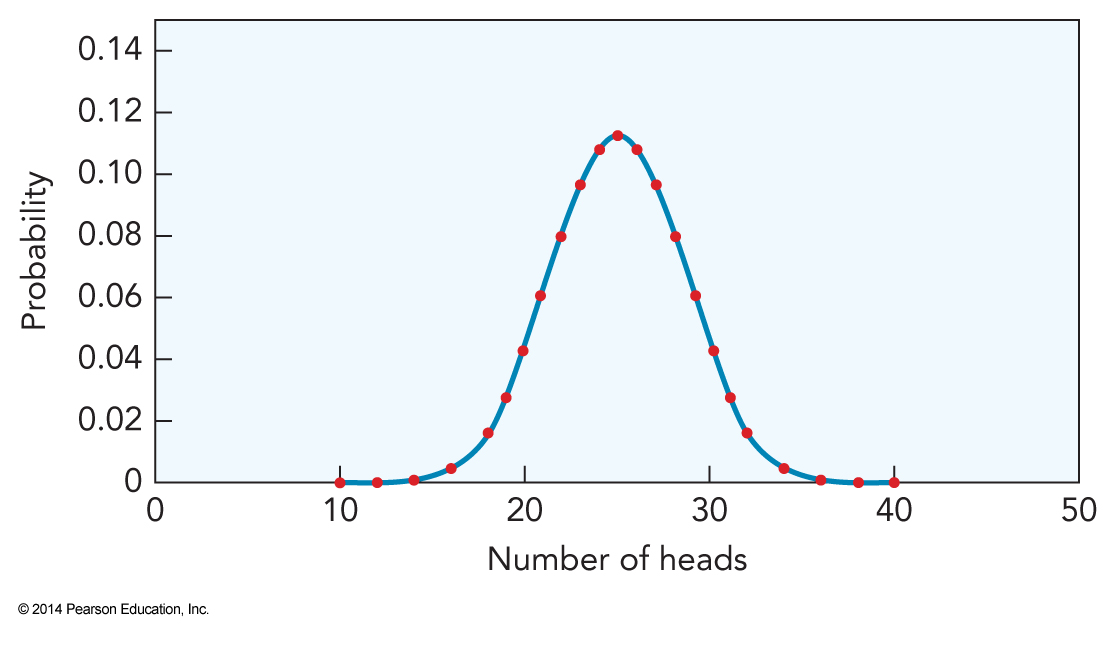
- The distribution of random events is a Gaussian function, a function of the form \(e^{-x^2}\)
- Our coin flipping curve is fit by $$ \sqrt{\frac{2}{\pi N}} e^{-\frac{2\left(h-\expect{h}\right)^2}{N}} $$
- \(h\) is the number of time we get a head
- \(\expect{h}\) is the mean value of \(h\)
- \(N\) is the number of coin flips
Derivation of Maxwell-Boltzmann Distribution
- Chapter 1 contains the original derivation of the distribution equation
- This is not a short derivation.
- It is covered on pages 50 – 53 of the textbook
- Rather than going through it all, I will summarize it
Summary of Maxwell-Boltzmann Distribution Derivation
- Maxwell assumed a Gaussian distribution for the particle velocities, \(v_x\), \(v_y\), and \(v_z\)
- To eliminate the dependence of direction, we integrated the distribution over all angles
- We solved for a constant \(a\)
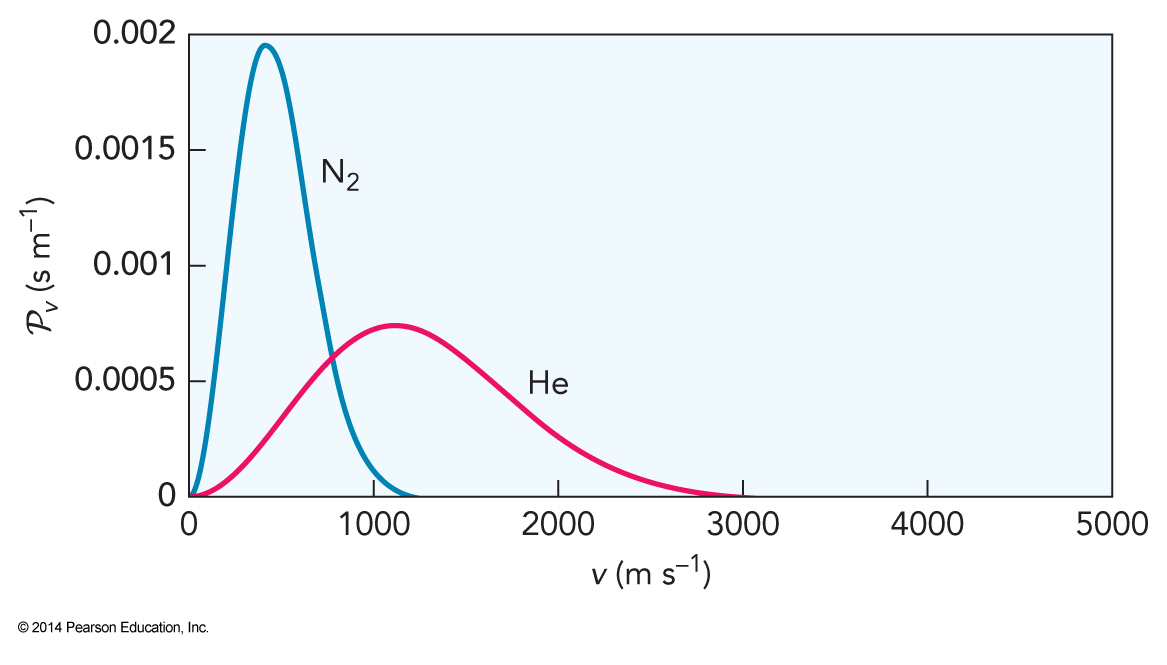
- Normalized the resulting function $$ \mathcal{P}_v(v)=4\pi \left( \frac{\mathcal{M}}{2\pi RT}\right)^{\frac{3}{2}} v^2 e^{-\frac{\mathcal{M}v^2}{2RT}} $$
The Maxwell-Boltzmann Distribution at 300 K
The Ideal Gas Law
- Reflections are totally elastic
- These reflection allow us to define the forces acting in the box
- The time-averaged force \(F_1\) exerted on wall 1 by a single particle with mass \(m\) traveling along the \(x\) axis at speed \(v_x\) is balanced by an equal and opposite force on the particle of \(–F_1\)
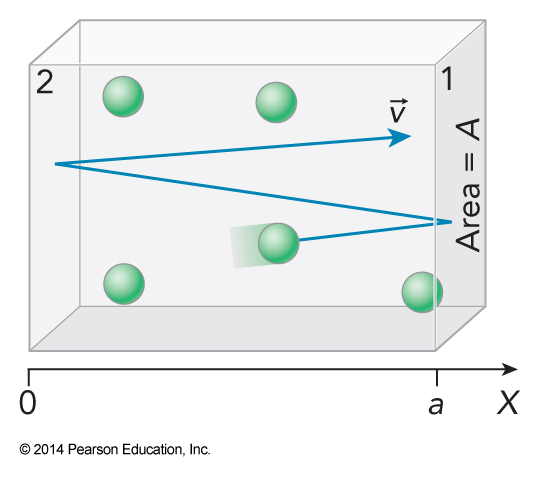
- This yields: $$ -F_1=ma_x=m\frac{dv_x}{dt} \approx m\frac{\Delta v_x}{\Delta t} = 2m\frac{-v_x}{\Delta t} $$
- \(\Delta t\) is the time of a single round trip between the walls
Continuing with the force
- Remembering that the box is \(a\) long in the \(x\) axis $$ \Delta t = \frac{2a}{v_x} $$
- Plugging that in we find $$ F_1 = 2m\frac{v_x}{\Delta t} = 2m\frac{v_x}{\bfrac{2a}{v_x}} = \frac{mv_x^2}{a} $$
- To extend this to the entire gas $$ \expect{F} = N\expect{F_1} = N \expect{\frac{mv_x^2}{a}} = \frac{Nm\expect{v_x^2}}{a} $$
Working with the velocity part of the expression
- The overall mean squared speed, \( \expect{v_x^2} \), can be separated $$ \expect{v^2} = \expect{v_x^2+v_y^2+v_z^2} = \expect{v_x^2} + \expect{v_y^2} + \expect{v_z^2} $$
- The motion on each of the axes should be exactly the same so all these means are equal, thus $$ \expect{v^2} = 3\expect{v_x^2} $$
- It turns out that for ideal gases $$ \expect{v^2} = \frac{3RT}{\mathcal{M}} $$
Continuing on...
- Combining out equations $$ \expect{F} = \frac{Nm\expect{v_x^2}}{a} = \frac{NmRT}{\mathcal{M}a} = \frac{n\mathcal{M}RT}{\mathcal{M}} = \frac{nRT}{a} $$
- Now we can solve for pressure $$ P=\frac{\expect{F}}{A} = \frac{nRT}{aA} = \frac{nRT}{V} $$
- This yields our well known ideal gas law $$ PV = nRT $$
Another Maxwell-Boltzmann Distribution
- We can write the Maxwell-Boltzmann equation in terms of kinetic energy of the molecules rather than molecular speeds $$ \mathcal{P}_v(v) = 4\pi \left( \frac{\mathcal{M}}{2\pi RT} \right)^\bfrac{1}{2} \left(\frac{E_m}{\pi RT}\right) e^{-\bfrac{E_m}{RT}} $$
- \(E_m\) is the molar energy
Chemical Equilibrium
- At equilibrium, the concentrations of products and reactants does not change
- The balance between the reactant and product concentrations is determined by the rate of motion of the atoms $$ \frac{\conc{products}}{\conc{reaectants}} \approx \frac{e^{-\bfrac{E_{prod}}{RT}}}{e^{-\bfrac{E_{reac}}{RT}}} = e^{-\bfrac{\left( E_{prod} - E_{reac} \right)}{RT}} = e^{-\bfrac{\Delta_{rxn}E^\ominus}{RT}} $$
- \( \Delta_{rxn} E^\ominus \) - change in energy from react. to prod.
Other Conditions
- If the reaction is allowed to exchange heat and work with its surroundings then it is the change in the Gibbs free energy, \(\Delta_{rxn}G^\ominus\), that determines the balance between reactants and products
- For the equilibrium \( \chem{A\rightleftharpoons B} \), we express the equilibrium constant, \(K_{eq}\), as $$ K_{eq}=e^{-\bfrac{\Delta_{rxn}G^\ominus}{RT}}\approx \frac{\conc{B}}{\conc{A}} $$
Time-Dependent Chemical Reactions
- Without waiting for equilibrium we can study a reaction
- The rate a reaction occurs is given by the rate law $$ \chem{A\rightarrow B}\text{ yields }Rate=-\frac{d\conc{A}}{dt}=k\conc{A} $$
- \(k\) is the rate constant
- The rate constant obeys the Arrhenius equation $$ k=Ae^{-\bfrac{E_a}{RT}} $$
- \(E_a\) is the activation energy
Final Thoughts
- In equation after equation we find these exponential expression.
- The expressions pop up when studying different situations
- Why? How are they all connected?
- It is the job of physical chemistry to discover the how they are linked and use the links to improve our understanding of the nature of matter
/